Sommaire
- Chapitre 1 : Notions fondamentales
- Chapitre 2 : Architecture d'un ordinateur
- Chapitre 3 : Microprocesseur
- Chapitre 4 : Mémoires
- Chapitre 5 : L'architecture Core
- Chapitre 6 : Optimisation : au coeur du core
- Bibliographie
6. Optimisation : au coeur du core
celui qui porte à aider chaque enfant à trouver sa propre voie
et celui qui pousse à lui inculquer ce que soi-même on croit juste, beau et vrai
Nicolas Sarkozy, Lettre aux Educateurs
4 septembre 2007
6.1. Introduction
L'objet de ce chapitre est de familiariser l'utilisateur avec les techniques d'optimisation concernant :
- alignement et accès mémoire
- instructions et codages spécifiques
- la vectorisation avec les unités SSE
- librairies dédiées
6.1.1. Fiabiliser son programme
Un aspect souvent négligé en programmation est la mise au point de tests afin de vérifier les fuites mémoires (memory leaks) ou les accès en dehors de zones mémoires autorisées à être accèdées.
6.1.1.a Accès non autorisé
Voici un morceau de code qui peut mener à un arrêt brutal de votre programme (la fameuse segmentation fault sous Unix) :
// a.cpp
int main() {
int *tab = new int[10];
for (i=0; i!=11; ++i) tab[i]=0;
return 0;
}
On accède ici à tab[10], ce qui n'est normalement pas autorisé. Votre programme peut alors posséder deux comportements différents :
- malgrè l'erreur, le programme fonctionne correctement, car la donnée que vous modifiez n'a pas d'influence sur d'autres programmes
- le programme produit une erreur de segmentation car vous modifiez une donnée en mémoire qui est vitale
Pour déterminer les erreurs de ce type vous pouvez utiliser ElectricFence. ElectricFence est une librairie qui intercepte les allocations mémoires et détermine quand vous procédez à un accès en dehors de zones allouées. Pour utiliser ElectricFence vous pouvez, soit réaliser l'édition de lien avec la version statique de la librairie :
> g++ -o a.exe a.cpp -lefence -ggdb
> gdb a.exe
(gdb) run
Starting program: /home/richer/tmp/a.exe
[Thread debugging using libthread_db enabled]
[New Thread -1211124016 (LWP 7616)]
Electric Fence 2.1 Copyright (C) 1987-1998 Bruce Perens.
Program received signal SIGSEGV, Segmentation fault.
[Switching to Thread -1211124016 (LWP 7616)]
0x08048566 in main () at a.cpp:6
4 for (int i=0;i!=11;++i) tab[i]=0;
(gdb) print i
$1 = 10
ou utiliser la librairie dynamique à l'intérieur d'un débogueur, ddd par exemple. Avant de lancer l'exécution du programme, tapez la commande suivante à l'intérieur du debogueur :
set environment LD_PRELOAD=/usr/lib/libefence.so.0.0
6.1.1.b Fuite mémoire (memory leak)
Une fuite mémoire correspond à un espace alloué dynamiquement que l'on a oublié de libéré par la suite. Cela peu amener votre programme a utiliser énormément de mémoire et réduire ainsi ses performances.
Il existe cependant un moyen très simple de détecter les fuites mémoires potentielles en utilisant valgrind :
valgrind --leak-check=full ./a.exe
==7862== Memcheck, a memory error detector.
==7862== Copyright (C) 2002-2006, and GNU GPL'd, by Julian Seward et al.
==7862== Using LibVEX rev 1658, a library for dynamic binary translation.
==7862== Copyright (C) 2004-2006, and GNU GPL'd, by OpenWorks LLP.
==7862== Using valgrind-3.2.1-Debian, a dynamic binary instrumentation framework.
==7862== Copyright (C) 2000-2006, and GNU GPL'd, by Julian Seward et al.
==7862== For more details, rerun with: -v
==7862==
==7862==
==7862== ERROR SUMMARY: 0 errors from 0 contexts (suppressed: 23 from 1)
==7862== malloc/free: in use at exit: 40 bytes in 1 blocks.
==7862== malloc/free: 1 allocs, 0 frees, 40 bytes allocated.
==7862== For counts of detected errors, rerun with: -v
==7862== searching for pointers to 1 not-freed blocks.
==7862== checked 134,252 bytes.
==7862==
==7862== 40 bytes in 1 blocks are definitely lost in loss record 1 of 1
==7862== at 0x4021A55: operator new[](unsigned) (vg_replace_malloc.c:195)
==7862== by 0x8048550: main (a.cpp:4)
==7862==
==7862== LEAK SUMMARY:
==7862== definitely lost: 40 bytes in 1 blocks.
==7862== possibly lost: 0 bytes in 0 blocks.
==7862== still reachable: 0 bytes in 0 blocks.
==7862== suppressed: 0 bytes in 0 blocks.
==7862== Reachable blocks (those to which a pointer was found) are not shown.
==7862== To see them, rerun with: --show-reachable=yes
6.1.2. Profilage
L'optimisation du code est un art, mais celle-ci ne doit pas intervenir lors de la création d'un programme mais une fois que le programme fonctionne correctement.
Pour optimiser un programme il faut tout d'abord déterminer quelles parties consomment le plus de temps CPU. C'est ce que l'on appelle le profilage (profiling) du programme.
Compiler le programmme à optimiser avec les options -pg. Exemple avec le programme suivant qui calcule la suite de fibonacci en utilisant une fonction récursive et une fonction itérative (fib.c) :
- CODE
- fib.c
- #include <stdio.h>
- #include <stdlib.h>
- int fib_recurs(int n) {
- if (n==0) return 0;
- if (n==1) return n;
- return fib_recurs(n-1) + fib_recurs(n-2);
- }
- int fib_iterat(int n) {
- int i;
- int *tab;
- tab[0] = 0;
- tab[1] = 1;
- tab[2] = 1;
- i = 2;
- while (i<=n) {
- tab[i] = tab[i-1] + tab[i-2];
- ++i;
- }
- return tab[n];
- }
- int main() {
- int n_recurs;
- int n_iterat;
- n_recurs = fib_recurs(40);
- n_iterat = fib_iterat(40);
- return 0;
- }
gcc -pg -o fib.exe fib.c
./fib.exe
gprof fib.exe >fib_result.txt
Le fichier résultat fib_result.txt montre que la fonction récursive prend plus de temps que la fonction itérative, ce qui est normal :
- fib_recurs : 8.13s (self seconds), appelée 331_160_280 fois
- fib_iterat : 0.14s (self seconds), appelée 1 fois
Flat profile:
Each sample counts as 0.01 seconds.
% cumulative self self total
time seconds seconds calls s/call s/call name
98.37 8.13 8.13 1 8.13 8.13 fib_recurs(int)
1.63 8.27 0.14 1 0.14 0.14 fib_iterat(int)
% the percentage of the total running time of the
time program used by this function.
cumulative a running sum of the number of seconds accounted
seconds for by this function and those listed above it.
self the number of seconds accounted for by this
seconds function alone. This is the major sort for this
listing.
calls the number of times this function was invoked, if
this function is profiled, else blank.
self the average number of milliseconds spent in this
ms/call function per call, if this function is profiled,
else blank.
total the average number of milliseconds spent in this
ms/call function and its descendents per call, if this
function is profiled, else blank.
name the name of the function. This is the minor sort
for this listing. The index shows the location of
the function in the gprof listing. If the index is
in parenthesis it shows where it would appear in
the gprof listing if it were to be printed.
Call graph (explanation follows)
granularity: each sample hit covers 4 byte(s) for 0.12% of 8.27 seconds
index % time self children called name
[1] 100.0 0.00 8.27 main [1]
8.13 0.00 1/1 fib_recurs(int) [2]
0.14 0.00 1/1 fib_iterat(int) [3]
-----------------------------------------------
331160280 fib_recurs(int) [2]
8.13 0.00 1/1 main [1]
[2] 98.4 8.13 0.00 1+331160280 fib_recurs(int) [2]
331160280 fib_recurs(int) [2]
-----------------------------------------------
0.14 0.00 1/1 main [1]
[3] 1.6 0.14 0.00 1 fib_iterat(int) [3]
-----------------------------------------------
This table describes the call tree of the program, and was sorted by
the total amount of time spent in each function and its children.
Each entry in this table consists of several lines. The line with the
index number at the left hand margin lists the current function.
The lines above it list the functions that called this function,
and the lines below it list the functions this one called.
This line lists:
index A unique number given to each element of the table.
Index numbers are sorted numerically.
The index number is printed next to every function name so
it is easier to look up where the function in the table.
% time This is the percentage of the `total' time that was spent
in this function and its children. Note that due to
different viewpoints, functions excluded by options, etc,
these numbers will NOT add up to 100%.
self This is the total amount of time spent in this function.
children This is the total amount of time propagated into this
function by its children.
called This is the number of times the function was called.
If the function called itself recursively, the number
only includes non-recursive calls, and is followed by
a `+' and the number of recursive calls.
name The name of the current function. The index number is
printed after it. If the function is a member of a
cycle, the cycle number is printed between the
function's name and the index number.
For the function's parents, the fields have the following meanings:
self This is the amount of time that was propagated directly
from the function into this parent.
children This is the amount of time that was propagated from
the function's children into this parent.
called This is the number of times this parent called the
function `/' the total number of times the function
was called. Recursive calls to the function are not
included in the number after the `/'.
name This is the name of the parent. The parent's index
number is printed after it. If the parent is a
member of a cycle, the cycle number is printed between
the name and the index number.
If the parents of the function cannot be determined, the word
`' is printed in the `name' field, and all the other
fields are blank.
For the function's children, the fields have the following meanings:
self This is the amount of time that was propagated directly
from the child into the function.
children This is the amount of time that was propagated from the
child's children to the function.
called This is the number of times the function called
this child `/' the total number of times the child
was called. Recursive calls by the child are not
listed in the number after the `/'.
name This is the name of the child. The child's index
number is printed after it. If the child is a
member of a cycle, the cycle number is printed
between the name and the index number.
If there are any cycles (circles) in the call graph, there is an
entry for the cycle-as-a-whole. This entry shows who called the
cycle (as parents) and the members of the cycle (as children.)
The `+' recursive calls entry shows the number of function calls that
were internal to the cycle, and the calls entry for each member shows,
for that member, how many times it was called from other members of
the cycle.
Index by function name
[3] fib_iterat(int) [2] fib_recurs(int)
6.1.3. Utilisation de VTune Analyzer (Intel)
VTune est un outil complet de profiling et de tuning qui permet de déterminer les hot spots et d'éclairer sur leur comportement : instruction peu performante, accès mémoire non aligné, nombre important de défauts de cache dus à des données de trop grande taille.
cas de prog.c
- Call Graph Wizard
- Sampling Wizard (% utilisation par sous-programme)
- Sampling Wizard (proc3, code source)
- Sampling Wizard (proc3, code source et assembleur)
cas de popcount
Pour rappel, cette fonction compilée avec des options de compilation différentes donnait des résultats de 8s ou 23s.
push ebp
xor ecx,ecx
mov ebp,esp
mov edx,DWORD PTR [ebp+8]
L1:
movzx eax,dl
movsx eax,BYTE PTR [eax+0x8048bd0]
add ecx,eax
shr edx,0x8
test edx,edx ; sans cette instruction 23s
; avec cette instruction 8s
jne L1
pop ebp
mov eax,ecx
ret
Une rapide analyse sous VTune, nous donne les résultats suivants pour les compteurs choisis :
| compteur | sans | avec |
| RAT_STALL.ANY % | 97 | 41 |
| RAT_STALL.FLAGS % | 98 | 38 |
| RAT_STALL_FLAGS events | 38.000 106 | 35 106 |
- RAT_STALL.FLAGS : compte le nombre de cycles durant lesquels l'exécution est suspendue en raison d'un accès partiel au registre des FLAGS
Selon Intel, les facteurs les plus importants pour optimiser les performances d'un cpu sont les suivants :
- bonne prédiction de branchement
- éviter les accès mémoires qui provoquent des attentes
- obtenir de bonnes performances dans le calcul des nombres réels
- vectorisation
6.2. Accès et utilisation de la mémoire
6.2.1. Alignement mémoire
Nous avons déjà évoqué dans le chapitre 3, les problèmes liés à l'alignement des données en mémoire. Nous savons qu'il est préférable d'aligner les données sur une adresse multiple de 2, 4, 8 ou 16.
Plusieurs possibilités d'alignement existent :
- utilisation des options en ligne de commande du compilateur pour aligner le code :
où n représente une puissance de 2.gcc -falign-functions=n -falign-jumps=n -falign-labels=n -falign-loops=n
- utilisation des directives du compilateur pour aligner les données :
- gcc / g++ :
int j __attribute__((aligned(16))); - icc / icpc / icl :
int j _declspec(align(16));
- gcc / g++ :
- lors de l'allocation mémoire, les données sont alignées mais pas forcément sur la puissance de 2 désirée, notamment pour les données qui seront utilisées par les unités SSE. On peut réaliser un alignement à la main comme suit ou utiliser _mm_malloc:
#include <stdio.h> #include <stdlib.h> #define malloc_align(p,q,T,size,align) \ printf("allocate %d bytes\n", size); \ p = (T *) malloc(size + align-1); \ q = (T *) (((int)p+align-1) & ~(align-1)); \ printf("unaligned @ %p\n", p); \ printf("aligned @ %p\n", q); int main() { int i; int *tab_unaligned, *tab; malloc_align(tab_unaligned, tab, int, 10*sizeof(int), 16); for (i=0; i<10; ++i) tab[i] = i; free(tab_unaligned); return 0; }le résultat en sortie de ce programme est (par exemple) :
allocate 40 bytes unaligned @ 0x804a008 aligned @ 0x804a010
ou plus simplement :
#include <xmmintrin.h>
int *tab;
tab = (int *) _mm_malloc(1024 * sizeof(int), 16);
...
_mm_free(tab);
6.2.2. La Multi-allocation ou allocation par blocs
Cette technique que je qualifie de multi-allocation, consiste à éviter de perdre du temps lors de nombreuses allocation/déallocation de la mémoire. Elle repose sur les principes suivants :
- les objets sont alloués par blocs et non pas un à un
- les objets ne sont pas libérés mais placés dans une liste chaînées (liste des éléments disponibles et réutilisables) lorsqu'ils ne sont plus utilisés
Cette technique possède des avantages et des inconvénients :
- + lors de l'allocation, on réalise une allocation de N objets plutôt que N allocations de 1 objet
- + lors de la désallocation, on place l'élément au début de la liste, on ne perd pas de temps à faire un appel système
- - les objets sont toujours présents en mémoire
Voici deux exemples, l'un en C l'autre en C++ :
- exemple en C : multi_alloc.h et multi_alloc.c (en HTML : multi_alloc.h et multi_alloc.c)
- exemple en C++ : multi_alloc.tgz (Attention! ne pas définir de destructeur pour la classe Complex pour que cela fonctionne)
6.3. Optimisation du code
6.3.1. Optimisation des instructions
Vous trouverez beaucoup d'informations sur le site d'Agner Fog, notamment dans les sections Optimizing subroutines in assembly language: An optimization guide for x86 platforms et The microarchitecture of Intel, AMD and VIA CPUs: An optimization guide for assembly programmers and compiler makers.
6.3.1.a élimination des sauts
Trouver la valeur minimum entre 2 valeurs non signées :
uint32_t a, b;
if (a < b) {
return a;
} else {
return b;
}
mov eax, [a]
mov ebx, [b]
cmp eax, ebx
jle .endif
else:
mov eax, ebx
endif
sub eax, ebx ; = a-b
sbb edx, edx ; = (b > a) ? 0xFFFFFFFF : 0
and edx, eax ; = (b > a) ? a-b : 0
add ebx, edx ; Result is in ebx
ou encore avec CMOVcc
cmp eax, ebx
cmovg eax, ebx
Il existe également l'instruction SETcc (set byte on condition)
X = (A < B) ? CONST1 : CONST2;
global main
section .data
A: dd 2
B: dd 1
CONST1 EQU 10
CONST2 EQU 30
CONST3 EQU -20
section .text
main:
xor ebx,ebx
mov eax,[A]
cmp eax,[B]
setge bl
sub ebx,1
and ebx,CONST3 ; CONST3 = CONST1-CONST2
add ebx,CONST2
Comme A > B, SETge fixe BL à 1, on soustrait ensuite 1, donc EBX=0, au final EBX=CONST2
Dans le cas contraire, BL=0, on soustraint 1 EBX, donc EBX = 0xFFFFFFFF, au final EBX=CONST1
6.3.1.b LEA (Load Effective Address)
L'instruction LEA est très utile car elle permet de regrouper :
- un décalage (1,2 ou 3 bits)
- deux additions
- et un déplacement
Par exemple, la série d'instructions suivantes :
mov eax,ecx
shl eax,3
add eax,ebx
add eax,200
peut être remplacée par :
lea eax,[ebx+ecx*8+200]
Attention : les symboles [] ne signifient pas qu'il faut charger dans eax la donnée pointée par l'expression entre les crochets, mais calculer ebx+ecx*8+200 et mettre ce résultat dans eax.
De même :
imul eax,5
peut être remplacée par :
lea eax,[eax+eax*4]
6.3.1.c inc et dec
Les instructions inc et dec ne modifient pas le drapeau de retenue (carry flag) mais sont susceptibles de modifier d'autres drapeaux, cela correspond à ne modifier qu'une partie du registre des flags et cela se traduit par un coût d'une micro-opération supplémentaire sur Pentium 4 et des délais d'attente sur Penitum II, III et M si une autre instruction tente de lire le registre de flags.
La documentation Intel stipule :
INC : Adds 1 to the destination operand, while preserving the state of the CF flag. The
destination operand can be a register or a memory location. This instruction allows a
loop counter to be updated without disturbing the CF flag. (Use a ADD instruction
with an immediate operand of 1 to perform an increment operation that does updates
the CF flag.)
6.3.1.d division
La division entière DIV et en flottant est généralement très pénalisante, bien plus que la multiplication. Il existe cependant quelques astuces qui permettent de simplifier la division.
a) division entière par puissance de 2
On sait que diviser X par 2N consiste à décaler la représentation binaire de X de N rangs vers la droite :
mov eax,X
shr eax,N
b) division entière par une constante
Dans le cas où on divise par une constante, il est possible de remplacer la division par une multiplication. Pour calculer q = X / d pour une représentation de l'information sur w bits, on calcule la valeur :
on multiplie ensuite X par f et on décale à droite de r positions.
l'algorithme est le suivant :
- b = (nombre de bits significatifs de d) - 1
- r = w + b
- f = 2r / d
- si f est en entier alors d est une puissence de 2 :
result = x shr b - sinon si la partie fractionnaire de f < 0.5 alors
arrondir f à l'entier k (k < f) le plus proche
result = ((X+1) × f) shr r - sinon (f > 0.5) alors :
arrondir f à l'entier k (k > f) le plus proche
result = (X × f) shr r
example : on désire diviser par 5 sur 32 bits :
- 510 = 1012
- b = 3 - 1 = 2
- r = 32 + 2 = 34
- f = 234 / 5 = 3435973836.8 = CCCCCCCC,CCCCCCCCD16
- k = CCCCCCCD16
6.3.1.e instruction assembleur sans équivalent dans les langages de haut niveau
Voici un exemple ou une instruction assembleur n'a pas d'équivalent dans un langage comme le C. L'instruction bsr (voir aussi bsf) calcule la position du bit le plus significatif de son opérande.
On peut programmer cette fonction en C :
long i;
for (i = (number >> 1), position = 0; i != 0; ++position) i >>= 1;
Une autre solution consiste à inclure du code assembleur à l'intérieur d'un morceau de code en C :
asm ("bsrl %1, %0" : "=r" (position) : "r" (number));
La solution n'est pas la meilleure en terme de portabilité, mais en C on peut contourner la difficulté en utilisant les directives de compilation en fonction de l'architecture.
Voir également les fonction builtin de gcc comme __builtin_popcount (unsigned int x)
| Code en C | Code asm | |
| Temp d'exécution | 28 s | 2,88 s |
Autres instructions : POPCNT, CRC32, LZCNT, CMPXCHG, BTR, BTS, BTC, BT, ...
6.3.2. Optimisation des boucles
6.3.2.a Cas général
for (int i = 0; i < n; i++) {
// (loop body)
}
Dont la traduction basique est :
mov edx, n ; Load n
xor ecx, ecx ; i=0
.for_begin:
cmp ecx, edx ; i < n ?
jge .for_end ; Exit when i >= n
; (loop body) ; Loop body goes here
add ecx, 1 ; i++
jmp .for_begin ; Jump back
.for_end:
Sur certaines architectures, on préfère utiliser add eax,1 plutôt que inc eax,1, car l'instruction inc a un problème pour accèder et mettre à jour une partie des flags, ce qui la rend moins efficace.
L'autre problème est le fait que l'on trouve 2 instructions de saut jge et jmp. On écrira donc :
mov edx, n ; Load n
test edx, edx ; Test n
jz .for_end ; Skip if n <= 0
xor ecx, ecx ; i = 0
.for_begin:
; (loop body) ; Loop body goes here
add ecx, 1 ; i++
cmp ecx, edx ; i < n ?
jl .for_begin ; Loop back if i < n
.for_end:
6.3.2.b dépliage de boucle
Pour tirer le maximum des unités vectorielles, il faut éviter d'écrire :
double a[100], sum;
int i;
sum = 0.0f;
for (i = 0; i < 100; i++) {
sum += a[i];
}
et déplier les boucles :
double a[100], sum1, sum2, sum3, sum4, sum;
int i;
sum1 = 0.0;
sum2 = 0.0;
sum3 = 0.0;
sum4 = 0.0;
for (i = 0; i < 100; i + 4) {
sum1 += a[i];
sum2 += a[i+1];
sum3 += a[i+2];
sum4 += a[i+3];
}
sum = (sum4 + sum3) + (sum1 + sum2);
Autre exemple tiré du Software Optimization Guide for AMD64 Processors. Sur l'exemple suivant, il vaut mieux réaliser un dépliage de 2 :
double a[MAX], b[MAX];
for (int i=0; i < MAX; ++i) {
a[i] = a[i] + b[i];
}
// a remplacer par
for (int i=0; i < MAX; i+=2) {
a[i] = a[i] + b[i];
a[i+1] = a[i+1] + b[i+1];
}
Le premier exemple est traduit par une boucle comportant 7 instructions. Sachant que les Athlon64 sont capables de décoder 3 instructions par cycle d'horloge et que l'unité arithmétique sur les réels n'est capable de réaliser qu'une addition par cycle, on en déduit que l'efficacité de cette boucle est de 3/7 addition par cycle soit 0,429 add/s.
mov ecx,MAX
mov eax,a
mov ebx,b
add_loop:
fld QWORD [eax]
fadd QWORD [ebx]
fstp QWORD [eax]
add eax,8
add ebx,8
dec ecx
jnz add_loop
En dépliant la boucle, on utilise 10 instructions et on réalise 2 additions par itération de la boucle, cela donne alors une efficacité de 6/10 addition par cycle, soit 0,6 add/s
shr ecx,1
add_loop:
fld QWORD [eax]
fadd QWORD [ebx]
fstp QWORD [eax]
fld QWORD [eax+8]
fadd QWORD [ebx+8]
fstp QWORD [eax+8]
add eax,16
add ebx,16
dec ecx
jnz add_loop
Autre exemple de dépliage par le compilateur :
int function(int *x, int size) {
int i, sum = 0;
for (i = 0; i < size; ++i) {
sum += x[i];
}
return sum;
}
; gcc -S -masm=intel -O3 for_loop.c -m32 -funroll-loops --param max-unroll-times=4
.file "for_loop.c"
.intel_syntax noprefix
.text
.p2align 4,,15
.globl function
.type function, @function
function:
.LFB0:
.cfi_startproc
push esi
.cfi_def_cfa_offset 8
.cfi_offset 6, -8
push ebx
.cfi_def_cfa_offset 12
.cfi_offset 3, -12
mov eax, DWORD PTR [esp+16] ; size
mov esi, DWORD PTR [esp+12] ; x
test eax, eax
jle .L4 ; sort de la fonction avec 0 comme résultat
lea ecx, [-4+eax*4] ; ecx = size*4 - 4
lea ebx, [esi+eax*4] ; ebx = esi + size * 4
mov eax, DWORD PTR [esi]
shr ecx, 2
lea edx, [esi+4]
and ecx, 3
cmp edx, ebx
je .L2
test ecx, ecx
je .L3
cmp ecx, 1
je .L14
cmp ecx, 2
.p2align 4,,3
je .L15
add eax, DWORD PTR [edx]
lea edx, [esi+8]
.L15:
add eax, DWORD PTR [edx]
add edx, 4
.L14:
add eax, DWORD PTR [edx]
add edx, 4
cmp edx, ebx
je .L2
.L3:
add eax, DWORD PTR [edx]
add edx, 16
add eax, DWORD PTR [edx-12]
add eax, DWORD PTR [edx-8]
add eax, DWORD PTR [edx-4]
cmp edx, ebx
jne .L3
.L2:
pop ebx
.cfi_remember_state
.cfi_restore 3
.cfi_def_cfa_offset 8
pop esi
.cfi_restore 6
.cfi_def_cfa_offset 4
ret
.p2align 4,,7
.p2align 3
.L4:
.cfi_restore_state
xor eax, eax
jmp .L2
.cfi_endproc
.LFE0:
.size function, .-function
.ident "GCC: (Ubuntu 4.8.2-19ubuntu1) 4.8.2"
.section .note.GNU-stack,"",@progbits
6.3.2.c blocage / tuilage (loop blocking / tiling)
Le blocage de boucle est une technique d'optimisation des performances de la mémoire. L'objectif du blocage de boucle consiste à éliminer le plus possible de défauts de cache. On transforme ici le problème initial en plusieurs sous-problèmes de manière à ne travailler que sur une partie de la mémoire :
Prenons l'exemple suivant :
float A[MAX][MAX], B[MAX][MAX];
for (i=0; i < MAX; i++) {
for (j=0; j < MAX; j++) {
A[i][j] = A[i][j] + B[j][i];
}
}
Le code produit n'est pas efficace car on obtient énormément de défaut de cache. Il vaut mieux le réécrire sous la forme suivante :
float A[MAX][MAX], B[MAX][MAX];
for (i=0; i < MAX; i+=block_size) {
for (j=0; j < MAX; j+=block_size) {
for (ii=i; ii < i+block_size; ii++) {
for (jj=j; jj < j+block_size; jj++) {
A[ii][jj] = A[ii][jj] + B[jj][ii];
}
}
}
}
Exemple pour le produit de matrices :
const int BLOCK_SIZE = 32;
void matrix_product(float *a, float *b, float *c, int dim) {
for (int i=0; i<dim; i += BLOCK_SIZE) {
for (int j=0; j<dim; j += BLOCK_SIZE) {
for (int k=0; k<dim; ++k) {
//
for (int ii=i; ii<i+BLOCK_SIZE; ++ii) {
for (int jj=j; jj<j+BLOCK_SIZE; ++jj) {
c[ii*dim+jj] += a[ii*dim + k] * b[k*dim + jj];
}
}
}
}
}
}
6.3.3. Exemple concret sur le dépliage
On désire écrire un sous-programme qui réalise le produit de deux vecteurs $x$ et $y$ et stocke le résultat dans un troisième vecteur $z$ en faisant la somme avec $z$ :
void vector_sum(float *x, float *y, float *z, size_t size) {
for (size_t i = 0; i < size; ++i) {
z[i] = z[i] + x[i] * y[i];
}
}On supposera que les tableaux $x$, $y$ et $z$ sont alignés sur une adresse multiple de 16.
On désire déplier par 4 quelque soit la taille, pour ce faire on procède ainsi :
- on commence par déplier la boucle en faisant en sorte de s'arrêter sur un multiple de 4
- on traite les itérations restantes
void vector_sum(float *x, float *y, float *z, size_t size) {
size_t i;
for (i = 0; i < multiple_of(size,4); i += 4) {
z[i + 0] += x[i + 0] * y[i + 0];
z[i + 1] += x[i + 1] * y[i + 1];
z[i + 2] += x[i + 2] * y[i + 2];
z[i + 3] += x[i + 3] * y[i + 3];
}
while (i < size) {
z[i] += x[i] * y[i];
++i;
}
}Ce que l'on peut réécrire en :
#define BODY(i) z[i] += x[i] * y[i];
void vector_sum(float *x, float *y, float *z, size_t size) {
size_t i;
for (i = 0; i < multiple_of(size,4); i += 4) {
BODY(i+0);
BODY(i+1);
BODY(i+2);
BODY(i+3);
}
while (i < size) {
BODY(i);
++i;
}
}La fonction multiple_of(i,4) peut être réalisée de plusieurs façons différentes, on considère ici que $a$ est une puissance de 2:
#define multiple_of(size, a) ((size / a) * a)#define multiple_of(size, a) (size & ~ (a-1))
Exemple avec 27 = 1.1011_b déplié par 4 :
- 27 = 4 * 6 + 3
- donc 27/4 = 6 itérations Unroll4 et reste 3 itérations Unroll1
- avec ~3, les deux derniers bits sont éliminés, reste donc 24 = 1.1000_d
Voici quatre implantations : x87, sse, avx, avx + fma :
- ; void vector_sum_prod_x87(float *x, float *y, float *z, size_t size)
- ; unroll by 4
- ; esi = x [ebp + 8]
- ; edi = y [ebp + 12]
- ; ebx = z [ebp + 16]
- ; edx = size [ebp + 20]
- ; ecx = i
- vector_sum_prod_x87:
- push ebp
- mov ebp, esp
- push esi
- push edi
- push ebx
- mov esi, [ebp + 8]
- mov edi, [ebp + 12]
- mov ebx, [ebp + 16]
- mov edx, [ebp + 20]
- xor ecx, ecx
- test edx, edx
- jz .end
- and edx, ~3
- cmp edx, 4
- jl .last
- .while_u4:
- fld dword [esi + ecx * 4]
- fmul dword [edi + ecx * 4]
- fadd dword [ebx + ecx * 4]
- fstp dword [ebx + ecx * 4]
- fld dword [esi + ecx * 4 + 4]
- fmul dword [edi + ecx * 4 + 4]
- fadd dword [ebx + ecx * 4 + 4]
- fstp dword [ebx + ecx * 4 + 4]
- fld dword [esi + ecx * 4 + 8]
- fmul dword [edi + ecx * 4 + 8]
- fadd dword [ebx + ecx * 4 + 8]
- fstp dword [ebx + ecx * 4 + 8]
- fld dword [esi + ecx * 4 + 12]
- fmul dword [edi + ecx * 4 + 12]
- fadd dword [ebx + ecx * 4 + 12]
- fstp dword [ebx + ecx * 4 + 12]
- add ecx, 4
- cmp ecx, edx
- jl .while_u4
- .last:
- mov edx, [ebp+20]
- .while_u1:
- cmp ecx, edx
- jge .end
- fld dword [esi + ecx * 4]
- fmul dword [edi + ecx * 4]
- fadd dword [ebx + ecx * 4]
- fstp dword [ebx + ecx * 4]
- inc ecx
- jmp .while_u1
- .end:
- pop ebx
- pop edi
- pop esi
- mov esp, ebp
- pop ebp
- ret
- ; void vector_sum_prod_sse(float *x, float *y, float *z, size_t size)
- ; use xmm registers and sse instructions
- ; esi = x [ebp + 8]
- ; edi = y [ebp + 12]
- ; ebx = z [ebp + 16]
- ; edx = size [ebp + 20]
- ; ecx = i
- vector_sum_prod_sse:
- push ebp
- mov ebp, esp
- push esi
- push edi
- push ebx
- mov esi, [ebp + 8]
- mov edi, [ebp + 12]
- mov ebx, [ebp + 16]
- mov edx, [ebp + 20]
- xor ecx, ecx
- test edx, edx
- jz .end
- and edx, ~3
- cmp edx, 4
- jl .last
- .while_u4:
- movaps xmm0, [esi + ecx * 4]
- movaps xmm1, [edi + ecx * 4]
- movaps xmm2, [ebx + ecx * 4]
- mulps xmm0, xmm1
- addps xmm2, xmm0
- movaps [ebx + ecx * 4], xmm2
- add ecx, 4
- cmp ecx, edx
- jl .while_u4
- .last:
- mov edx, [ebp+20]
- .while_u1:
- cmp ecx, edx
- jge .end
- fld dword [esi + ecx * 4]
- fmul dword [edi + ecx * 4]
- fadd dword [ebx + ecx * 4]
- fstp dword [ebx + ecx * 4]
- inc ecx
- jmp .while_u1
- .end:
- pop ebx
- pop edi
- pop esi
- mov esp, ebp
- pop ebp
- ret
- ; void vector_sum_prod_avx(float *x, float *y, float *z, size_t size)
- ; use ymm registers and avx instructions
- ; esi = x [ebp + 8]
- ; edi = y [ebp + 12]
- ; ebx = z [ebp + 16]
- ; edx = size [ebp + 20]
- ; ecx = i
- vector_sum_prod_avx:
- push ebp
- mov ebp, esp
- push esi
- push edi
- push ebx
- mov esi, [ebp + 8]
- mov edi, [ebp + 12]
- mov ebx, [ebp + 16]
- mov edx, [ebp + 20]
- xor ecx, ecx
- test edx, edx
- jz .end
- and edx, ~7
- cmp edx, 4
- jl .last
- .while_u8:
- vmovaps ymm0, [esi + ecx * 4]
- vmovaps ymm1, [edi + ecx * 4]
- vmovaps ymm2, [ebx + ecx * 4]
- vmulps ymm0, ymm1
- vaddps ymm2, ymm0
- vmovaps [ebx + ecx * 4], ymm2
- add ecx, 8
- cmp ecx, edx
- jl .while_u8
- .last:
- mov edx, [ebp+20]
- .while_u1:
- cmp ecx, edx
- jge .end
- fld dword [esi + ecx * 4]
- fmul dword [edi + ecx * 4]
- fadd dword [ebx + ecx * 4]
- fstp dword [ebx + ecx * 4]
- inc ecx
- jmp .while_u1
- .end:
- pop ebx
- pop edi
- pop esi
- mov esp, ebp
- pop ebp
- ret
- ; void vector_sum_prod_fma(float *x, float *y, float *z, size_t size)
- ; use ymm registers and avx instructions + fma
- ; esi = x [ebp + 8]
- ; edi = y [ebp + 12]
- ; ebx = z [ebp + 16]
- ; edx = size [ebp + 20]
- ; ecx = i
- vector_sum_prod_fma:
- push ebp
- mov ebp, esp
- push esi
- push edi
- push ebx
- mov esi, [ebp + 8]
- mov edi, [ebp + 12]
- mov ebx, [ebp + 16]
- mov edx, [ebp + 20]
- xor ecx, ecx
- test edx, edx
- jz .end
- and edx, ~7
- cmp edx, 4
- jl .last
- .while_u8:
- vmovaps ymm0, [esi + ecx * 4]
- vmovaps ymm1, [edi + ecx * 4]
- vmovaps ymm2, [ebx + ecx * 4]
- vfmadd231ps ymm2, ymm0, ymm1
- vmovaps [ebx + ecx * 4], ymm2
- add ecx, 8
- cmp ecx, edx
- jl .while_u8
- .last:
- mov edx, [ebp+20]
- .while_u1:
- cmp ecx, edx
- jge .end
- fld dword [esi + ecx * 4]
- fmul dword [edi + ecx * 4]
- fadd dword [ebx + ecx * 4]
- fstp dword [ebx + ecx * 4]
- inc ecx
- jmp .while_u1
- .end:
- pop ebx
- pop edi
- pop esi
- mov esp, ebp
- pop ebp
- ret
6.4. Librairies C/C++ et librairies dédiées
6.4.1. La librairie C
Il est préférable d'utiliser les sous-programmes de base comme memmove pour déplacer des zones de mémoire ou memcpy pour recopier une zone de mémoire. Ces sous-programmes ont été optimisés.
Remplacer :
int *dst, *src;
for (i = 0; i < N; ++i) {
dst[i] = src[i]
}
par
memcpy(dst, src, N * sizeof(int));
6.4.2. La librairie C++ STL
La STL (Standard Template Library) est la librairie C++ standard et contient un nombre important de containers (vector, list, dequeue, map, multimap), ainsi que des algorithmes s'applicant sur ces containers. La STL est sensée être fiable et efficace.
6.4.3. Autres librairies
Un grand nombre d'algorithmes ont été étudiés et améliorés de manière à obtenir des temps d'exécution minimaux.
- BLAS (Basic Linear Algebra) est une bibliothèque de sous-programmes liés au calcul vectoriel et matriciel.
- LAPACK (Linear Algebra PACKage) écrite en Fortran 77, concerne la résolution de systèmes d'équations linéaires, recherche de valeurs propres, factorisation de matrices,... LAPACK utilise une partie des sous-programmes de BLAS
Différentes implémentations de BLAS/LAPACK existent et dépendent du processeur utilisé :
Voici un petit exemple de produit matriciel qui utilise le sous-programme SGEMM (Single floating-point GEneral Matrix matrix Multiplication) de la librairie Intel MKL :
int size; // size of square matrix
float *A; // first square matrix
float *B; // second square matrix
float *C; // result
mkl_set_num_threads(2);
// compute C = alpha * A * B + beta * C
cblas_sgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
size, size, size,
1.0, /* alpha */
A, size,
B, size,
0.0, /* beta */
C, size);
On compile le programme avec les librairies suivantes :
ALL=C icpc -o main.exe obj/*.o -O3 -axT -msse2
-Wl,--start-group
/opt/intel/mkl/10.0.011/lib/32/libmkl_core.a
/opt/intel/mkl/10.0.011/lib/32/libmkl_intel.a
/opt/intel/mkl/10.0.011/lib/32/libmkl_blacs.a
/opt/intel/mkl/10.0.011/lib/32/libmkl_lapack.a
/opt/intel/mkl/10.0.011/lib/32/libmkl_intel_thread.a
/opt/intel/mkl/10.0.011/lib/32/libmkl_scalapack.a
-Wl,--end-group -lguide -lpthread
Avec icc version 13.01 :
-Wl,--start-group
/opt/intel/mkl/lib/ia32/libmkl_core.a
/opt/intel/mkl/lib/ia32/libmkl_intel.a
/opt/intel/mkl/lib/ia32/libmkl_blacs.a
/opt/intel/mkl/lib/ia32/libmkl_blacs_intelmpi.a
/opt/intel/mkl/lib/ia32/libmkl_intel_thread.a
/opt/intel/mkl/lib/ia32/libmkl_scalapack_core.a
-Wl,--end-group -liomp5 -lpthread -ldl -lm
Voici quelques résultats :
| Processor | L2/L3 Cache | basic | BLAS (1 CPU) |
BLAS (2 CPU) |
BLAS (4 CPU) |
| C2D E6420 @ 2.13 Ghz FSB 1066 Mhz |
4 Mo | 3m23s | 5s24 | 3s08 | - |
| C2D E8400 @ 3.00 Ghz FSB 1333 Mhz |
6 Mo | 3m03s | 3s40 | ? | - |
| C2Q Q6600 @ 2.40 Ghz FSB 1066 Mhz |
8 Mo | 3m01s | 4s59 | 2s48 | 1s27 |
| C2Q Q9300 @ 2.50 Ghz FSB 1333 Mhz |
6 Mo | 3m03s | 4s21 | 2s26 | 1s27 |
| Processor | L2/L3 Cache | basic | inv jk | tile 32 | BLAS (1 CPU) |
BLAS (2 CPU) |
BLAS (4 CPU) |
| Core i5-3570k @ 3.40 Ghz ( 32 bits) |
256 ko/ 6 Mo | 3m50 | 26s | 19s | 1s265 | 0s838 | 0s442 |
| Core i5-4570 @ 3.20 Ghz (64 bits) |
256 ko / 6 Mo | 3m17s | 25s | 17s | 1s133 | 1s083 | 0s932 |
| Processor | L2 Cache | basic | BLAS (1 CPU) |
BLAS (2 CPU) |
BLAS (4 CPU) |
| C2D E6420 @ 2.13 Ghz FSB 1066 Mhz |
4 Mo | 8m50s | 12s26 | 6s9 | - |
| C2D E8400 @ 3.00 Ghz FSB 1333 Mhz |
6 Mo | 8m01s | 11s32 | 4s3 | - |
| C2Q Q6600 @ 2.40 Ghz FSB 1066 Mhz |
8 Mo | 7m27s | 10s74 | 5s54 | 2s92 |
| C2Q Q9300 @ 2.50 Ghz FSB 1333 Mhz |
6 Mo | 7m22s | 10s07 | 5s11 | 2s71 |
On remarquera que :
- bien que le Core 2 Duo E8400 fonctionne à une fréquence de 3 Ghz, il obtient des temps de calcul plus importants que le Core 2 Quad Q6600 qui ne fonctionne qu'à 2,4 Ghz. Cela est du principalement à la taille du cache L2 qui est de 8 Mo sur le Quad Core alors qu'il n'est que de 6 Mo sur le Dual Core
- la fréquence du FSB ne semble pas influencer les résultats puisque le Q6600 et le Q9300 obtienent sensiblement les mêmes résultats
6.5. Savoir utiliser le compilateur
L'utilisation des options en ligne de commande des compilateurs permet parfois de simplifier l'optimisation. Par exemple, le compilateur C Intel (icc ou icpc pour le C++), offre différents types d'optimisations :
- optimisation interprocédurale
- optimisation guidée par le profilage
- optimisation des boucles (vectorisation)
6.5.1. Options de compilation de gcc / g++<
Le compilateur gcc possède un certain nombre d'options qui permettent d'améliorer l'optimisation du code :
- -O2 optimisations de niveau 2
- -O3 optimisations de niveau 3 (inclu le niveau 2)
- -falign-functions=n où n est une puissance de 2, alignement du début du code des fonctions
- -falign-loops=n de même pour les boucles
- -ftree-loop-optimize permet de déplacer les constantes hors des boucles, simplification du test de sortie
- -floop-block réalise le loop blocking
- -funroll-loops --param max-unroll-times=8 dépliage des boucles uniquement si le nombre d'itérations est connu lors de la compilation
- -funroll-all-loops dépliage des boucles même si le nombre d'itérations n'est pas connu lors de la compilation
Pour chaque architecture, on dispose également d'un certain nombre d'options d'optimisation :
-mtune=i386,i586,i686,pentium2,pentium3,pentium4,pentium-m,athlon,athlon64génère du code pour l'architecture spécifiée-march=..sur le même modèle que -mtune-mfpmath=387,ssecalcul sur les réels avec coprocesseur ou unités SSE-mmmx, -msse, -msse2, -msse3, -m3dnow-m32, -m64génère du code pour une architecture 32 ou 64 bits- ensemble d'options qui semblent donner de bons résultats :
-O3 -fno-thread-jumps -fno-guess-branch-probability -fno-cprop-registers -fno-if-conversion -fno-delayed-branch -foptimize-sibling-calls -fcse-follow-jumps -fgcse -fexpensive-optimizations -fstrength-reduce -frerun-cse-after-loop -frerun-loop-opt -fcaller-saves -fpeephole2 -fregmove -fstrict-aliasing -freorder-blocks -fsched-spec -freorder-functions -falign-loops -funit-at-a-time -fprefetch-loop-arrays -fno-inline -fpeel-loops -ftracer -funswitch-loops -fbranch-target-load-optimize -mno-push-args -mno-align-stringops -mfpmath=387 -fno-math-errno -fno-trapping-math -ffinite-math-only - réaliser l'édition de liens éventuellement avec
-lrt -lm
voir la documentation de gcc (version 4.2.1) pour plus de renseignements ou consulter le livre : The Definitive Guide to GCC de William Von Hagen, Apress, 2006, ISBN 1-59059-585-8.
6.5.2. Options de compilation de icc, icpp les compilateurs Intel
6.5.2.a Optimisation interprocédurale (-ip, -ipo)
sur les architectures de type IA-32, elle concerne :
- le passage d'arguments de sous-programmes dans des registres plutôt que dans la pile
- le déplacement d'invariants en dehors des boucles
6.5.2.b Optimisation guidée par le profilage
ce type d'optimsation se déroule en 3 phases :
- compiler en utilisant l'option -prof_gen
- exécuter le programme, un fichier .dyn est alors généré qui contient des informations qui sont utilisées dans la phase suivante
- recompiler avec -prof-use qui prend en compte les informations générées durant l'exécution
6.5.2.c Auto vectorisation et parallélisation
Voir Auto vectorization et Auto parallelization
6.6. En dehors du Core : la programmation GPU (GPU Programming/Computing)
Le GPU computing est destiné à accélérer les algorithmes massivement parallèles en profitant des nombreuses unités d'exécution présentes au seun d'un GPU. Ces algorithmes doivent être conçus de manière à se décompose en une multitude de petits threads qui seront exécutés en parallèle, par groupes, sur le GPU... Une façon de penser et de programmer totalement différente donc qui a demandé à NVidia de concevoir un langage adapté : C pour CUDA. Celui-ci a été écrit par Ian Buck, qui était à l'origine de Brook GPU, un langage destiné à exploiter le pipeline de rendu 3D, et non directement le coeur de calcul du GPU, ce qui le rendait plus rigide et moins performant.
(Citation: Hardware.fr, Damien Triolet)
L'idée de la programmation GPU repose sur l'utilisation des circuits GPU (Graphical Processing Unit) des cartes graphiques. En effet, ces circuits se révèlent très performants pour réaliser du calcul vectoriel ou matriciel.
Par exemple, dans le cas de la multiplication matricielle, la société GPU-Tech annonce en novembre 2007 des temps 10 foix supérieurs à un CPU pour des flottants en simple précision. Sur un AMD Athlon 64 3800+, on obtient les résultats suivants :
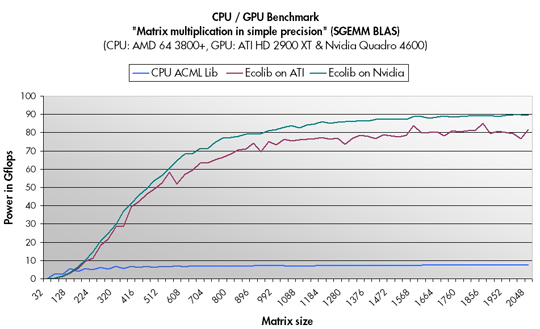
Image du site GPU-Tech
La difficulté de la programmation GPU est de faire cohabiter un CPU avec GPU.
quelques transparents :
Les dernière cartes NVidia (Turing, 2018) les plus puissantes sont les RTX 2080 Ti:
- 4352 CUDA cores
- 10 Giga rays / s
- 11 Go de GDDR6
- résolution: 7680x4320
- 14.2 TFLOPS1 of peak single precision (FP32) performance
- 28.5 TFLOPS1 of peak half precision (FP16) performance
- 113.8 Tensor TFLOPS
Voir le CUDA C Programming Guide
6.6.1. Application Folding@Home
Le projet Folding@Home (2000) vise à étudier le repliement des protéines. Lorsque des protéines ne se replient pas correctement ou ne sont pas correctement formées, elles peuvent engendrer des maladies (Alzheimer, Encéphalopathie spongiforme bovine (Mad Cow Disease), Parkinson, Myopathie, ...).
Le problème lié au repliement des protéines est qu'il demande énormément de temps de calcul. L'idée du projet Folding@Home a été de demander à des particuliers de télécharger sur leur ordinateur un programme qui s'exécute lorsque la machine est en veille, et effectue des calculs. On dispose ainsi qu'une importante source de calculateurs.
Historique des améliorations du programme de calcul :
- 2000 : Tinker engine
- 2003 : Gromacs, utilisation de code assembleur (à la main) + instructions SSE (amélioration d'un facteur de 20 à 30 par rapport à Tinker)
- 2006 : utilisation de la carte graphique ATI X1900 (nouvelle amélioration d'un facteur de 20 à 30)
6.7. Exemples liés à la vectorisation
6.7.1. parallel and
On désire améliorer le traitement de base suivant qui consiste à réaliser un and entre deux vecteurs de caractères :
// vecteurs de propriétés chez des individus
void fitch_parsimony(char *vA, char *vB, char *vC, int len) {
int i;
for (i = 0; i < len; i++) {
vC[i] = vA[i] & vB[i];
}
}
On compare plusieurs implantations dont celles utilisant l'instruction SSE pand qui permet de réaliser le AND en parallèle entre 16 octets.
| Amélioration | Pentium-M | Pentium III | Pentium 4 | Pentium D | C2D E6420 | Athlon 64 | Sempron |
| -O2 | 27.450s | 276s | 38.296 | 24.794 | 17.917s | 28.186 | 36.549 |
| dépliage 4 | 21.561s | - | 34.956 | 21.313 | 18.065 | 25.110 | 33.130 |
| dépliage 8 | 21.413s | - | 35.123 | 20.749 | 17.877 | 24.166 | 32.302 |
| dépliage 16 | 21.221s | - | 35.068 | 20.969 | 17.881 | 24.338 | 32.310 |
| traite par 4 (eax) | 16.881s | - | 33.043 | 17.969 | 5.380 | 24.718 | 32.466 |
| traite par 4 (eax) + dépliage 4 |
6.624s | 185.0 | 30.713 | 14.605 | 5.244 | 19.597 | 28.974 |
| vectorisation (sse2) | 5.788s (-80%) |
179.0 (-33%) |
29.125 (-22%) |
15.085 (-39%) |
4.004 (-77%) |
20.157 (-28%) |
29.846 (-19%) |
| vectorisation (sse2) + unroll 4 |
6.044s | 182.0 | 28.757 | 14.997 | 4.028 | 20.329 | 29.710 |
| Amélioration | E8400 | Q6600 | Q9300 | P9500 | Core i7 860 | Core i5 3570k |
| -O2 | 12.62s | 15.84s | 15.77s | 18.15s | 13.38s | 10.10s |
| dépliage 4 | 12.65s | 16.06s | 15.88s | 10.09s | 7.27s | 8.71s |
| dépliage 8 | 12.64s | 15.73s | 15.29s | 14.50s | 10.11s | 8.11s |
| dépliage 16 | 12.40s | 15.91s | 15.20s | 14.10s | 10.12s | 7.62s |
| traite par 4 (eax) | 7.92s | 4.82s | 4.56s | 6.48s | 5.34s | 2.69s |
| traite par 4 (eax) + dépliage 4 |
3.88s | 4.58s | 4.66s | 8.99s | 10.37s | 2.28s |
| vectorisation (sse2) | 2.98s (-77%) |
3.64s (-77%) |
3.54s (-77%) |
3.22s (-82%) |
2.00s (-85%) |
1.53s (-84%) |
| vectorisation (sse2) + unroll 4 |
3.00s | 3.68s | 3.47s | 3.22s | 1.92s | 1.53s |
- Pentium III Tualatin, 1.4 Ghz, FSB 100/133 Mhz, 256 Mo SDRAM PC 100
- Pentium-M, 2.0 Ghz, FSB 533 Mhz, 1 Go DDR-SDRAM
- Pentium 4 Northwood, 2.8 Ghz, FSB 800 Mhz, 256 Mo DDR-SDRAM PC3200
- Pentium D 830 Smithfield, 3 Ghz, FSB 800 Mhz, 1 Go DDR2-SDRAM PC4300
- Core 2 Duo E6420, 2.13 Ghz, FSB 1066 Mhz, 2 Go DDR2-SDRAM PC 6400
- Core 2 Duo E8400, 3.00 Ghz, FSB 1333 Mhz, 3 Go DDR2-SDRAM PC 6400
- Core 2 Quad Q6600, 2.40 Ghz, FSB 1066 Mhz, 3 Go DDR2-SDRAM PC 5300
- Core 2 Quad Q9300, 2.50 Ghz, FSB 1333 Mhz, 3 Go DDR2-SDRAM PC 6400
- Athlon 64 X2 4200+, 4.2 Ghz (2.2 Ghz), FSB 400 Mhz, 512 Mo DDR-SDRAM PC 3200
- Sempron 3000+, FSB 400 Mhz, 512 Mo DDR-SDRAM PC 3200
- Intel Core 2 Duo P9500, 2.53 Ghz, FSB 800 Mhz, 4 Go DDR2-SDRAM
- Intel Core i7 860, 2.8 Ghz, 4 Go DDR3-SDRAM PC1333
- Intel Core i5-3570K CPU @ 3.40GHz
- Intel Atom N450, 1.66 Ghz, 1 Go RAM (Mini PC)
sources disponibles.
Ces résultats nous amènent à faire les remarques suivantes :
- le dépliage a une faible influence et permet de gagner quelques % excepté sur le Core 2 Duo (!)
- le traitement par groupe de 4 octets (et non un par un) peut avoir une influence importante
- l'utilisation des instructions SSE est intéressante et apporte un gain égal au traitement par 4 + dépliage
Avec gcc 4.6.3 si on compile avec -O3 -msse2, alors sous Core i5-3570K, les temps de calculs pour toutes les méthodes varient de 1.54s à 1.57s !
6.7.2. problème de la recherche du maximum de parcimonie
On désire améliorer le traitement de base suivant qui consiste à calculer le score de parcimonie de deux séquences d'acides aminés.
int fitch_parsimony(char *x, char *y, char *z, int size) {
int i, mutations = 0;
for (i = 0; i < size; i++) {
z[i] = x[i] & y[i];
if (z[i] == 0) {
z[i] = x[i] | y[i];
++mutations;
}
}
return mutations;
}
6.7.2.a Results for parsimony version 2013
see technical report 2013/06/24-1
In the following tables:
- columns %sse2 (resp. %avx et %avx2) represent the improvement in percentage:
(C_reference - asm_sse2) / C_reference * 100 - columns improvement factor sse2 (resp. avx et avx2) are the ratio:
(C_reference / asm_sse2)
| i5-4570 3.20GHz |
i5-3570K 3.40GHz |
i7-2600 3.40GHz |
i7-860 2.80GHz |
Q9300 2.50GHz |
Q6600 2.40GHz |
Pentium D 3.00GHz |
Sempron 3000 1.8GHz |
|
| C_reference | 106.610 | 115.630 | 112.470 | 139.040 | 197.800 | 182.080 | 258.290 | 206.420 |
| C_reference_optimized | 116.240 | 111.900 | 106.860 | 140.480 | 203.140 | 177.030 | 249.630 | 211.390 |
| C_optimized_1 | 53.030 | 62.300 | 60.810 | 131.480 | 219.230 | 188.640 | 169.630 | 209.950 |
| C_optimized_2 | 5.300 | 7.630 | 6.780 | 9.900 | 18.660 | 23.180 | 38.960 | 41.260 |
| asm_sse2 | 4.960 | 5.500 | 5.660 | 7.820 | 16.600 | 15.620 | 26.570 | 46.610 |
| intrinsics_sse2 | 3.330 | 4.290 | 3.980 | 6.500 | 35.930 | 38.200 | 64.640 | 78.080 |
| asm_sse41 | 4.880 | 5.240 | 4.960 | 7.240 | 16.340 | -- | -- | -- |
| intrinsics_sse41 | 3.740 | 4.640 | 4.260 | 7.440 | 45.850 | -- | -- | -- |
| asm_sse42 | 4.950 | 5.330 | 5.090 | 6.770 | -- | -- | -- | -- |
| intrinsics_sse42 | 3.760 | 4.650 | 4.380 | 7.210 | -- | -- | -- | -- |
| asm_avx | 2.940 | 3.640 | 3.500 | -- | -- | -- | -- | -- |
| intrinsics_avx | 3.290 | 3.710 | 3.640 | -- | -- | -- | -- | -- |
| asm_avx2 | 2.220 | -- | -- | -- | -- | -- | -- | -- |
| intrinsics_avx2 | 2.810 | -- | -- | -- | -- | -- | -- | -- |
| % sse2 | 95.35 | 95.24 | 94.97 | 94.38 | 91.61 | 91.42 | 89.71 | 77.42 |
| improvement factor sse2 | 21.49 | 21.02 | 19.87 | 17.78 | 11.92 | 11.66 | 9.72 | 4.43 |
| % avx | 97.24 | 96.85 | 96.89 | -- | -- | -- | -- | -- |
| improvement factor avx | 36.26 | 31.77 | 32.13 | -- | -- | -- | -- | -- |
| % avx2 | 97.92 | -- | -- | -- | -- | -- | -- | -- |
| improvement factor avx2 | 48.02 | -- | -- | -- | -- | -- | -- | -- |
| i5-4570 3.20GHz |
i5-3570K 3.40GHz |
i7-2600 3.40GHz |
i7-860 2.80GHz |
Q9300 2.50GHz |
Q6600 2.40GHz |
Pentium D 3.00GHz |
Sempron 3000 1.8GHz |
|
| C_reference | 210.410 | 233.130 | 230.750 | 279.610 | 414.690 | 364.860 | 518.650 | 421.710 |
| C_reference_optimized | 215.940 | 226.720 | 213.160 | 284.280 | 407.700 | 355.910 | 503.490 | 431.930 |
| C_optimized_1 | 105.800 | 124.500 | 118.100 | 269.190 | 433.830 | 377.460 | 339.110 | 424.750 |
| C_optimized_2 | 9.580 | 14.640 | 13.020 | 19.170 | 30.580 | 44.970 | 77.660 | 93.590 |
| asm_sse2 | 9.430 | 10.280 | 10.780 | 14.850 | 32.270 | 28.580 | 52.810 | 103.750 |
| intrinsics_sse2 | 6.200 | 8.160 | 7.640 | 11.570 | 88.170 | 75.130 | 128.820 | 161.450 |
| asm_sse41 | 9.340 | 9.980 | 9.230 | 10.920 | 30.810 | -- | -- | -- |
| intrinsics_sse41 | 6.990 | 8.740 | 8.030 | 13.410 | 71.730 | -- | -- | -- |
| asm_sse42 | 9.430 | 10.070 | 9.440 | 12.280 | -- | -- | -- | -- |
| intrinsics_sse42 | 6.940 | 8.710 | 8.110 | 13.300 | -- | -- | -- | -- |
| asm_avx | 5.330 | 6.650 | 6.390 | -- | -- | -- | -- | -- |
| intrinsics_avx | 6.060 | 6.990 | 6.520 | -- | -- | -- | -- | -- |
| asm_avx2 | 3.920 | -- | -- | -- | -- | -- | -- | -- |
| intrinsics_avx2 | 4.910 | -- | -- | -- | -- | -- | -- | -- |
| % sse2 | 95.52 | 95.59 | 95.33 | 94.69 | 92.22 | 92.17 | 89.82 | 75.40 |
| improvement factor sse2 | 22.31 | 22.68 | 21.41 | 18.83 | 12.85 | 12.77 | 9.82 | 4.06 |
| % avx | 97.47 | 97.15 | 97.23 | -- | -- | -- | -- | -- |
| improvement factor avx | 39.48 | 35.06 | 36.11 | -- | -- | -- | -- | -- |
| % avx2 | 98.14 | -- | -- | -- | -- | -- | -- | -- |
| improvement factor avx2 | 53.68 | -- | -- | -- | -- | -- | -- | -- |
| i5-4570 3.20GHz |
i7-2600 3.40GHz |
i3-2375M 1.50GHz |
Phenom II X6 1090 T 3.2GHz |
|
| C_reference | 102.660 | 107.880 | 274.510 | 106.250 |
| C_reference_optimized | 92.040 | 107.900 | 233.550 | 111.230 |
| C_optimized_1 | 46.960 | 56.300 | 142.970 | 75.930 |
| C_optimized_2 | 9.640 | 48.320 | 29.890 | 57.490 |
| asm_sse2 | 3.540 | 3.780 | 9.720 | 5.850 |
| intrinsics_sse2 | 3.680 | 4.020 | 9.750 | 6.240 |
| intrinsics_sse41 | 4.200 | 4.670 | 11.010 | -- |
| intrinsics_avx | 3.540 | 3.590 | 9.140 | -- |
| asm_avx2 | 2.020 | -- | -- | -- |
| intrinsics_avx2 | 2.820 | -- | -- | -- |
| % sse2 | 96.55 | 96.50 | 96.46 | 94.49 |
| improvement factor sse2 | 29.00 | 28.54 | 28.24 | 18.16 |
| % avx | 96.55 | 96.67 | 96.67 | -- |
| improvement factor avx | 29.00 | 30.05 | 30.03 | -- |
| % avx2 | 98.03 | -- | -- | -- |
| improvement factor avx2 | 50.82 | -- | -- | -- |
Note that the C optimized 1 and C optimized 2 versions are different ways of coding the initial function, but the C optimized 2 can provide a significant improvement:
uint32_t parsimony_optimized_1(uint8_t *x, uint8_t *y, uint8_t *z, uint32_t size) {
uint32_t i, mutations=0;
for (i=0; i<size; ++i) {
unsigned char x_, y_;
uint32_t c;
x_ = x[i] & y[i];
y_ = x[i] | y[i];
z[i] = x_ | ((!x_) * y_);
c = ((!x_) & 1);
mutations += c;
}
return mutations;
}
uint32_t parsimony_optimized_2(uint8_t *x, uint8_t *y, uint8_t *z, uint32_t size) {
uint32_t i, mutations=0;
for (i=0; i<size; ++i) {
unsigned char x_, y_;
uint32_t c;
x_ = x[i] & y[i];
y_ = x[i] | y[i];
z[i] = (x_ == 0) ? y_ : x_;
c = ((!x_) & 1);
mutations += c;
}
return mutations;
}
6.10.2.2 Résultats pour la parcimonie version 2008 (SSE2)
| Amélioration | Pentium-M | Pentium III | Pentium 4 | Pentium D | C2D E6420 | Athlon 64 | Sempron |
| -O2 | 48.287s | - | 60.153 | 63.000 | 46.415 | 43.879 | 53.723 |
| dépliage 4 | 47.415 (-1.8%) |
- | 52.378 | 56.098 (-11%) |
44.959 (-3%) |
39.538 (-10%) |
48.675 |
| traite par 4 | 44.143s (-8.5%) |
- | 48.668 (-19%) |
55.027 (-12%) |
40.943 (-12%) |
37.726 (-14%) |
46.275 |
| vectorisation 1 (sse) | 14.265 | - | 38.286 | 40.012 | 9.025 | 11.953 | 16.409 |
| vectorisation 2 (sse) | 7.381s (-84%) |
- | 15.612 (-74%) |
8.825 (-85%) |
2.852 (-93%) |
11.869 (-72%) |
16.033 (-70%) |
| vectorisation 3 (sse) | 7.896s | - | 15.531 | 9.209 | 3.568 | 11.981 | 16.317 |
| vectorisation 4 (sse) | 7.704s | - | 15.730 | 9.269 | 2.998 | 11.753 | 16.033 |
| Amélioration | Atom N450 | C2D E8400 | C2Q Q6600 | C2Q Q9300 | C2Q P9500 | i7 860 | i5 3570K 3.40GHz |
i7 2600 3.40GHz |
i5 3570k 3.40GHz |
| -O2 | 79.42 | 29.22/43.80 | 40.91 | 39.35 | 37.76 | 30.58 | 28.39 | 26.06 | 28.66 |
| dépliage 4 | 69.05 | 28.36/42.45 (-3%) |
39.69 | 38.66 | 42.92 | 38.67 | 26.91 | 24.31 | 25.48 |
| traite par 4 | 73.96 | 31.22 | 36.50 | 36.17 | 33.71 | 28.39 | 21.71 | 10.60 | 10.12 |
| vectorisation 1 (sse) | 26.27 | 8.92 | 8.36 | 8.02 | 7.60 | 6.06 | 2.81 | 2.50 | 2.83 |
| vectorisation 2 (sse) | 19.17 (-75%) |
2.61 (-91%) |
2.47 (-93%) |
2.36 (-94%) |
2.23 (-94%) |
1.89 (-93%) |
1.45 (-94%) |
1.43 (-94%) |
1.45 (-94%) |
| vectorisation 3 (sse) | 19.25 | 3.33 | 3.12 | 2.99 | 2.85 | 2.20 | 1.92 | 1.86 | 1.92 |
| vectorisation 4 (sse) | 18.30 | 1.72 | 2.35 | 2.31 | 2.14 | 1.84 | 1.42 | 1.43 | 1.43 |
| vectorisation 2 (sse+POPCNT) | - | - | - | - | - | 1.49 (-95%) |
1.69 (-94%) |
1.88 (-93%) |
1.68 (-94%) |
| Amélioration | Pentium 997 @1.6Ghz | Intel i5 4570 3.2 Ghz |
| -O2 | 60.56 | 25.43 |
| dépliage 4 | 56.59 (-6%) |
22.90 |
| traite par 4 | 25.07 | 8.48 |
| vectorisation 1 (sse) | 6.10 | 2.91 |
| vectorisation 2 (sse) | 3.62 (-94%) |
1.26 (-95%) |
| vectorisation 3 (sse) | 4.56 | 1.78 |
| vectorisation 4 (sse) | 3.53 | 1.26 |
| vectorisation 2 (sse+POPCNT) | 4.64 | 1.54 |
Ces résultats nous amènent à faire les remarques suivantes :
- le dépliage ou le traitement par groupe de 4 octets (et non un par un) peuvent permettre de gagner de 10 à 20 %
- la vectorisation (méthode 1, utilisation de BT) est beaucoup moins efficace que les autres versions (table de conversion), sauf pour les AMD pour lesquels on obtient les mêmes résultats
- la vectorisation apporte un gain de 70 à 90 %
On notera que pour traite par 4, il existe une différence importante entre le core i5 et le core i7. Cette différence est due à l'utilisation de compilateurs différents.
Avec gcc 4.6.3 si on compile avec -O3 -msse2, alors sous Core i5-3570K, le compilateur n'est pas capable d'optimiser le traitement pour toutes les méthodes !
6.7.3. strlen avec registres SSE
Amélioration de la fonction strlen qui calcule la longueur d'une chaîne de caractères en langage C.
On utilise l'instruction BSF (Scans source operand for first bit set)
| Longueur | strlen | strlen_c | strlen_sse1 | strlen_sse2 | strlen_sse3 | strlen_scasb |
| 10 | 0.11 | 0.21 | 0.10 | 0.10 | 0.08 | 0.58 |
| 20 | 0.13 | 0.20 | 0.34 | 0.36 | 0.12 | 0.85 |
| 50 | 0.23 | 0.47 | 0.19 | 0.22 | 0.21 | 0.66 |
| 200 | 0.70 | 1.40 | 0.55 | 0.61 | 0.68 | 6.00 |
| 500 | 1.70 | 3.24 | 1.24 | 1.38 | 1.76 | 13.98 |
| 960 | 3.14 | 6.02 | 2.27 | 2.51 | 3.28 | 27.02 |
| Amélioration | Pentium-M | Pentium III | Pentium 4 | Pentium D | C2D E6420 | Athlon 64 | Sempron |
| strlen (std) | 4.936 | - | 4.454 | 4.264 | 3.144 | 4.884 | 6.284 |
| strlen (perso) | 9.529 | - | 7.475 | 7.752 | 5.820 | 9.077 | 11.745 |
| vectorisation (1) eax | 2.732 | - | 3.981 | 2.352 | 2.244 | 4.320 | 5.420 |
| vectorisation (2) ecx | 3.052 | - | 3.981 | 2.284 | 2.528 | 3.892 | 4.968 |
| vectorisation (3) bsf | 3.844 | - | 7.668 | 9.989 | 3.252 | 7.124 | 9.437 |
| repnz scasb | 18.793 | - | 14.358 | 12.953 | 26.410 | 9.553 | 12.149 |
- la fonction strlen de la librairie standard C est optimisée
- le temps de traitement de l'instruction bsf a été amélioré sur Pentium-M et Core 2 Duo
- la vectorisation + utilisation d'une table de conversion + eax se révèle la plus intéressante sauf pour les processeurs AMD
- sur Athlon 64 X2, la commande rep scasb est estimée prendre 15 + (5/2 × ECX) cycles horloge
6.7.4. multiple sequence alignment
Projet de programmation 2009-2010 : vectorisation de l'algorithme de programmation dynamique de Needleman et Wunsch.
| Méthode/CPU | Pentium D | Pentium-M | Q6600 | Q9300 | i7 860 | i7 2600k |
| method 1 (C code) | 56.67 | 21.79 | 18.98 | 17.74 | 13.28 | 12.32 |
| method 2 (asm vect unaligned) | 114.05 | 47.76 | 36.25 | 30.74 | 25.90 | 21.27 |
| method 3 (asm vect aligned) | 51.37 | 51.31 | 26.45 | 22.19 | 20.15 | 14.49 |
| method 4 (asm vect aligned version 2) | 27.26 | 38.43 | 18.76 | 15.46 | 12.45 | 10.00 |
| method 5 (asm vect aligned version 3) | 39.66 | 46.61 | 26.24 | 20.54 | 19.78 | 13.79 |
| method 6 (asm vect aligned version 4) | 23.90 | 39.04 | 17.55 | 14.60 | 10.66 | 7.86 |
| method 7 (asm vect aligned version 5) | - | - | - | 11.42 | 7.73 | 6.07 |
| gain (method 1/method 7) | - | - | - | - 35 % | - 41 % | - 50 % |
Description des algorithmes :
- method 1 : code C du sujet
- method 2 : traduction de method 1 avec données non alignées
- method 3 : traduction de method 1 avec données alignées
- method 4 : amélioration de method 3
- method 6 : amélioration de method 3
- method 7 : amélioration de method 3 avec utilisation d'instructions SSE4.1
Machines utilisées :
- Pentium-M, 2.0 Ghz, FSB 533 Mhz, 1 Go DDR-SDRAM
- Pentium D 830 Smithfield, 3 Ghz, FSB 800 Mhz, 1 Go DDR2-SDRAM PC4300
- Core 2 Quad Q6600, 2.40 Ghz, FSB 1066 Mhz, 3 Go DDR2-SDRAM PC 5300
- Core 2 Quad Q9300, 2.50 Ghz, FSB 1333 Mhz, 3 Go DDR2-SDRAM PC 6400
- Intel Core i7 860 @ 2.8 Ghz
6.7.5. chr_replace
Projet de programmation 2011-2012 : utilisation des instructions SSE pour remplacer un caractère par un autre dans une chaine (voir)
6.7.6. mesure
Projet de programmation 2013-2014 : utilisation des instructions SSE/AVX/AVX2 pour compter le nombre de caractères similaires (ou différents) entre deux chaines (voir)
6.7.7. solver
Dans le cadre de la mise au point d'un solver en calcul propositionnel on désire optimiser une fonction en la vectorisant (voir).
6.7.8. tri fusion avec vecteur SSE
Comment faire un tri fusion en utilisant des instructions SSE (voir).