Ecole Doctorale MaSTIC
- 12 et 13 Mai 2025
- 26 et 27 Juin 2024
Bâtiment H, Salle H113, Faculté des Sciences, Université d'Angers
Intervenant: Jean-Michel Richer
1.1. Cours
Vous trouverez une partie du cours ici.
1.2. Ressources
- List of Nvidia graphics processing units (Wikipedia)
- Quel GPU vous correspond le mieux ? (NVidia)
- GPU Specs Database (Tech Power Up)
1.3. Mise en application
Les travaux pratiques ont lieu en salle H113 qui comprend des machines dotées des caractéristiques suivantes :
- CPU : Intel(R) Core(TM) i7-8700 CPU @ 3.20GHz, 16 Go de RAM
- GPU : Quadro P2000 (Driver Version: 470.182.03, CUDA Version: 11.4, CC 6.1)
1.3.1. Somme de vecteurs
Il s'agit d'un exemple de base, classique, qui permet de comprendre l'enchaînement des opérations et l'interaction entre CPU et GPU.
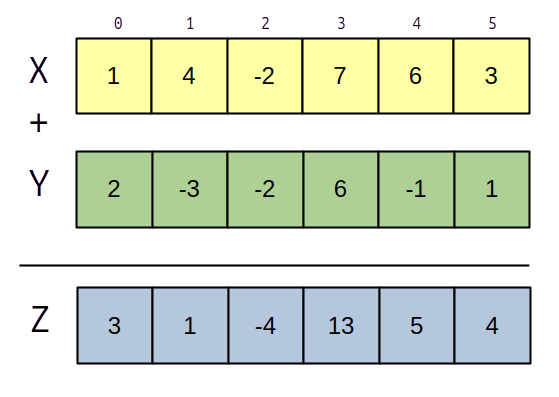
On dispose de trois vecteurs $x$, $y$ et $z$ de taille $N$ et on calcule :
$∀i ∈ [0..N[, z[i] = x[i] + y[i]$.
1.3.1.a Programme
Créer un programme appelé
./vec_sum.exe -n 1000000
Vous pouvez récupérer l'archive cuda_ed_etud.tgz qui contient quelques fichiers nécessaires à l'élaboration des programmes que nous allons mettre en oeuvre.
1.3.1.b Vecteurs sur le CPU
On définira le type
- #include <cstdint>
- #include <iostream>
- #include <iomanip>
- using namespace std;
- typedef float real;
- // équivalent du type size_t
- typedef uint32_t u32;
- // size of a vector as the number of elements
- u32 vec_size;
- // pointers to vectors that will be allocated
- real *cpu_vec_x;
- real *cpu_vec_y;
- real *cpu_vec_z;
Un fois qu'on a déterminé la taille des vecteurs (paramètre du programme), on peut allouer ceux-ci :
- cpu_vec_x = new real[vec_size];
- cpu_vec_y = new real[vec_size];
- cpu_vec_z = new real[vec_size];
puis les instancier :
- for (u32 i = 0; i < vec_size; ++i)
- {
- cpu_vec_x[i] = 0.1;
- cpu_vec_y[i] = 0.2;
- }
1.3.1.c Vecteurs sur le GPU
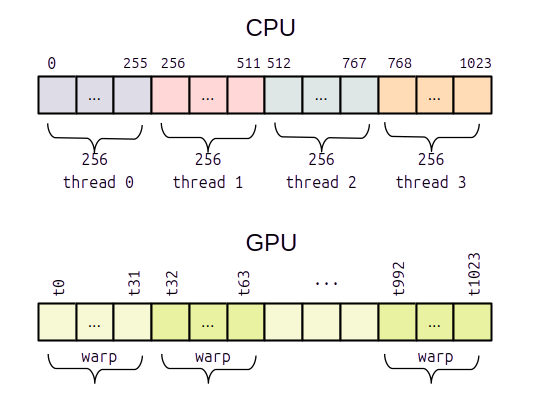
Parallélisme sur CPU et GPU
On commence par déclarer les vecteurs puis on les alloue sur le GPU :
- real *gpu_vec_x;
- real *gpu_vec_y;
- real *gpu_vec_z;
- cudaMalloc( (void **) &gpu_vec_x, vec_size * sizeof(real) );
- cudaMalloc( (void **) &gpu_vec_y, vec_size * sizeof(real) );
- cudaMalloc( (void **) &gpu_vec_z, vec_size * sizeof(real) );
Il faut ensuite copier les données des vecteurs $x$ et $y$ vers les vecteurs alloués sur le GPU :
- // cudaMemcpy(destination, source, taille en octets, sens de la copie)
- cudaMemcpy( gpu_vec_x, cpu_vec_x, vec_size* sizeof(real), cudaMemcpyHostToDevice );
- cudaMemcpy( gpu_vec_y, cpu_vec_y, vec_size* sizeof(real), cudaMemcpyHostToDevice );
Avant de lancer le kernel qui réalisera le calcul, on calcule le nombre de blocs en fonction de la taille d'un bloc. Dans le cas présent on prend un bloc de taille maximale c'est à dire de 1024 threads.
- int block_dim = 1024;
- int nbr_blocks = (vec_size + block_dim - 1) / block_dim;
On lance le kernel de calcul sur le GPU :
- kernel_sum<<<nbr_blocks, block_dim>>>( gpu_vec_x, gpu_vec_y, gpu_vec_z, vec_size );
Enfin on copie le résultat qui se trouve dans
- // cudaMemcpy(destination, source, taille en octets, sens de la copie)
- cudaMemcpy( cpu_vec_z, gpu_vec_z, vec_size* sizeof(real), cudaMemcpyDeviceToHost );
On affiche le vecteur obtenu :
- for (u32 i = 0; i < vec_size; ++i) {
- cout << i << " " << cpu_vec_z[i] << endl;
- }
On libère la mémoire :
- delete [] cpu_vec_x;
- delete [] cpu_vec_y;
- delete [] cpu_vec_z;
- cudaFree( gpu_vec_x );
- cudaFree( gpu_vec_y );
- cudaFree( gpu_vec_z );
1.3.1.d Le kernel
On utilise autant de threads que d'éléments dans le vecteur, le kernel s'écrit donc :
- __global__
- void kernel_sum( real *x, real *y, real *z, int size)
- {
- int tid = blockDim.x * blockIdx.x + threadIdx.x;
- if (tid < size) {
- z[tid] = x[tid] + y[tid];
- }
- }
1.3.1.e Compilation
On procède en deux étapes en utilisant
- on compile le fichier
vec_sum.cu avec l'option--compile et il faut indiquer pour quel type de GPU on compile le code en spécifiant la Compute Capability - on réalise l'édition de lien avec l'option
--link
- nvcc --compile -o vec_sum.o vec_sum.cu
- -gencode arch=compute_52,code=sm_52
- -gencode arch=compute_60,code=sm_60
- -gencode arch=compute_61,code=sm_61
- -gencode arch=compute_75,code=sm_75
- -gencode arch=compute_80,code=sm_80
- -gencode arch=compute_86,code=sm_86
- -std=c++11 -g -G -Xcompiler="-std=c++11 -O3 -Wall"
- nvcc --link -o vec_sum.exe vec_sum.o
Dans cet exemple on a spécifié plusieurs Compute Capability (CC = 5.2, 6.0, 6.1, 7.5, 8.0, 8.6) car on ne connaît pas le type de GPU utilisé. En général, on ne mettra qu'une seule CC, celle du GPU que l'on utilisera.
1.3.1.f Tests
Réaliser quelques tests avec des tailles de vecteurs de 1.000 puis 1.000.000 d'éléments.
Que remarque t-on ?
1.3.2. Réduction
1.3.2.a Principe
La réduction consiste à calculer, par exemple, la somme des éléments d'un vecteur :
$∀i ∈ [0..N[,\; sum = ∑↙{i=0}↖{n-1} z[i]$
La réduction est un algorithme problématique mais pour lequel on trouve rapidement des solutions qui permettent de conserver le parallèlisme.
1.3.2.b Sur le CPU
Sur un CPU doté de $k$ threads de calcul, on divisera le calcul de la réduction en $k$ sommes partielles, puis un seul thread réalisera la somme des sommes partielles.
- float sum = 0.0;
- #pragma omp for reduction(+ : sum)
- for (int i = 0; i < vec_size; ++i)
- {
- sum += z[i];
- }
1.3.2.c Première implantation sur le GPU
On peut reprendre ce principe sur GPU en utilisant un seul bloc de threads :
- __global__
- void kernel_reduction_1(real *z, int vec_size)
- {
- int tid = threadIdx.x;
- int i = tid + blockDim.x;
- while (i < vec_size) {
- z[tid] += z[i];
- i += blockDim.x;
- }
- }
Par exemple si on utilise un bloc de 1024 threads et des vecteurs de taille 10240, on parcourera 9 blocs, le premier bloc contiendra les sommes partielles.
On transfère le premier bloc vers le CPU qui réalise la somme des sommes partielles.
1.3.2.d Deuxième implantation sur le GPU
On va utiliser de la mémoire partagée, celle-ci agit comme une mémoire cache et son temps accès est de l'ordre de 10 à 20 cycles d'horloge, tandis que la mémoire GDDR peut avoir un temps d'accès de l'ordre de centaines de cycles d'horloge.
- __global__
- void kernel_reduction_2(real *z, int size) {
- // déclaration de la mémoire partagée
- // la taille n'est pas précisée, elle le sera
- // lors de l'appel du kernel
- extern __shared__ real shared_mem[];
- // thread index
- int tid = threadIdx.x;
- shared_mem[tid] = z[tid];
- // index;
- int i = tid + blockDim.x;
- while (i < size)
- {
- shared_mem[tid] += z[i];
- i += blockDim.x;
- }
- z[tid] = shared_mem[tid];
- }
- // l'appel au kernel se fait en précisant la taille de la mémoire partagée
- // en troisième paramètre ici un tableau de 1024 real, si block_size=1024
- kernel_reduc<<<1, block_size, block_size*sizeof(real)>>>(gpu_vec_z, vec_size);
L'influence de la mémoire partagée sera limitée puisqu'on accède principalement à la mémoire du GPU (GDDR).
Il faudra comme précédemment transférer le premier bloc vers la mémoire du CPU pour réaliser la somme des sommes partielles.
1.3.2.e Troisième implantation sur le GPU
Dans cette dernière approche qui est sensée être la plus rapide, la somme des sommes partielles est réalisée sur le GPU et est placée dans $z[0]$ :
- __global__
- void kernel_reduc(real *z, int size) {
- extern __shared__ real shared_mem[];
- // thread index
- int tid = threadIdx.x;
- shared_mem[tid] = z[tid];
- // index;
- int i = tid + blockDim.x;
- while (i < size)
- {
- shared_mem[tid] += z[i];
- i += blockDim.x;
- }
- // calcul de la somme des sommes partielles sur le GPU
- __syncthreads();
- int stride = blockDim.x / 2;
- while (stride > 0) {
- if (tid < stride) {
- shared_mem[tid] += shared_mem[tid + stride];
- }
- stride = stride / 2;
- __syncthreads();
- }
- if (tid == 0) {
- z[0] = shared_mem[0];
- }
- }
Ici il est nécessaire de synchroniser les calculs à chaque étape :
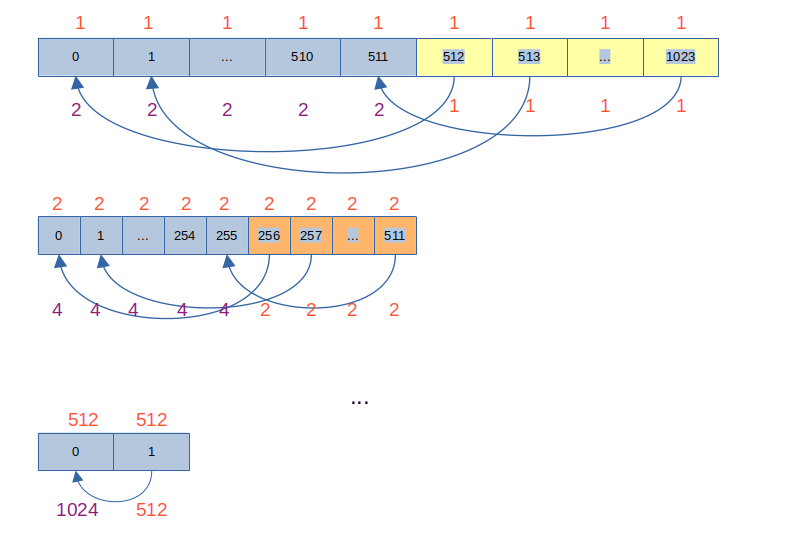
- au début
stride = 512 , on calcule donc :shared_mem[0] += shared_mem[512] shared_mem[1] += shared_mem[512+1] - ...
shared_mem[511] += shared_mem[512+511]
- puis on synchronize
__syncthreads() ce qui oblige à terminer tous les calculs avant de passer àstride = 256 - puis on divise
stride par 2, ce qui donnestride = 256 , on calcule donc :shared_mem[0] += shared_mem[256] shared_mem[1] += shared_mem[256+1] - ...
shared_mem[255] += shared_mem[256+255]
- etc
- jusqu'à ce qu'on arrive à
stride = 1 , on calcule donc :shared_mem[0] += shared_mem[1]
A chaque étape on divise le bloc en deux et on additionne la partie haute du bloc à la partie basse, puis on recommence.
La fonction
- la synchronisation de tous les threads dans un bloc donné. Lorsque cette fonction est appelée, tous les threads doivent atteindre cette instruction avant que l'exécution ne puisse continuer. Cela signifie que tous les threads du bloc doivent terminer leurs calculs jusqu'à ce point avant que tout thread puisse avancer.
- d'assurer la consistance de la mémoire partagée : toutes les écritures dans la mémoire partagée faites par les threads sont visibles par tous les autres threads du bloc. Cela est crucial lorsque les threads écrivent dans la mémoire partagée, puis lisent ces valeurs. Sans synchronisation, certains threads pourraient lire des valeurs non mises à jour.
1.4. Courbes de Julia
Voir ce TP.
Il s'agit d'un exemple typique de parallélisme ou le GPU peut se révéler plus intéressant que le CPU.
1.5. CUDA avec Python
Installer le module pycuda.
Voici un exemple avec la somme de vecteurs :
- import pycuda.autoinit
- import pycuda.driver as cuda
- import numpy as np
- from pycuda.compiler import SourceModule
- # Kernel CUDA pour additionner les vecteurs
- kernel_code = """
- __global__ void vector_sum(float *x, float *y, float *z, int size)
- {
- int tid = threadIdx.x + blockIdx.x * blockDim.x;
- if (tid < size)
- {
- z[tid] = x[tid] + y[tid];
- }
- }
- """
- # Taille des vecteurs
- n = 1024
- # Créer des vecteurs aléatoires
- a = np.random.randn(n).astype(np.float32)
- b = np.random.randn(n).astype(np.float32)
- c = np.zeros_like(a)
- # Allouer de la mémoire sur le GPU et copier les données
- a_gpu = cuda.mem_alloc(a.nbytes)
- b_gpu = cuda.mem_alloc(b.nbytes)
- c_gpu = cuda.mem_alloc(c.nbytes)
- cuda.memcpy_htod(a_gpu, a)
- cuda.memcpy_htod(b_gpu, b)
- # Compiler le kernel
- mod = SourceModule(kernel_code)
- vector_sum_kernel = mod.get_function("vector_sum")
- # Définir la taille du bloc et du grid
- block_size = 256
- grid_size = (n + block_size - 1) // block_size
- # Lancer le kernel
- vector_sum_kernel(a_gpu, b_gpu, c_gpu, np.int32(n), block=(block_size, 1, 1), grid=(grid_size, 1, 1))
- # Copier le résultat du GPU vers le CPU
- cuda.memcpy_dtoh(c, c_gpu)
- # Vérifier le résultat
- print("Vecteur a:", a)
- print("Vecteur b:", b)
- print("Somme a + b:", c)
1.6. Analyse
Comparer les caractéristiques des cartes suivantes :
- GeForce GTX 1660 Super
- GeForce RTX 3050 (2560 coeurs CUDA, 8 Go, GPU Part Number: 2507-150-A1)
- GeForce GTX 1070
- Quadro P2000
On s'intéressera notamment aux caractéristiques suivantes :
- année de production
- nombre de coeurs
- quantité de mémoire
- bande passante mémoire
- puissante en TFlops en simple et double précision
Combien de RTX 4090 faut-il pour égaler la puissance d'une A100 ?
1.7. Serveurs
- Vidéo : serveur à 1 million d'euros avec 8 GPU à 40.000 €
- Gaming server
- HGX server
1.8. Test comparatif
Test sur le calcul des ensembles de Julia pour une image de 4096x4096 et 10.000 itérations :
| Carte | float | double |
| GeForce 1660 Super | ? | ? |
| RTX 3050 6GB | 0,292 | 15,632 |
| GeForce RTX 2080 Ti | 0,222 | 5,488 |
| V100 PCIE-32GB | 0,284 | 0,780 |