5. Soustraction et Division Binaire





5.1. Soustraction

Le principe de la soustraction est le même qu'en décimal. Lorsque l'on calcule $25 - 16$, on commence à s'intéresser aux unités. $5$ étant inférieur à $6$, on ajoute une dizaine à $5$ et on calcule $15 - 6$ ce qui donne $9$. On passe ensuite aux dizaines. Sachant que l'on a ajouté une dizaine précédemment, on retire cette dizaine et on calcule $2 - 1$ auquel on retranche la dizaine, soit $2 - 1 - 1 = 0$.

Il suffit donc d'appliquer les régles suivantes :

Voyons cela sur un exemple et calculons $5 - 10$, soit en binaire sur 4 bits $0101_2 - 1010_2$. Dans ce cas on ne garde que les 4 premiers bits du résultats :

Retenue 1 1
0 1 0 1
- 1 0 1 0
= 1 0 1 1

Soit au final $1011_2$ qui dans le cadre de la représentation signée en complément à $2$ correspond à $-5$. On a donc bien le résultat escompté.

5.1.1. Soustraire 1

Pour soustraire $1$ d'un nombre binaire $x$, il suffit :

Par exemple :

5.2. Division

La division, tout comme en décimal, est difficile à appréhender. Elle consiste à diviser le dividende $n$ par le diviseur $d$ et obtenir un quotient $q$ ainsi qu'un reste $r$. On a donc $n = q × d + r$. On va considérer que $n >= d$ par la suite.

Comment divise t-on en binaire ? Il suffit de rechercher la position (numéro du bit) dans le dividende $n$ où il est possible de soustraire le diviseur $d$ le plus à gauche possible, puis d'effectuer la soustraction. On réitère ensuite l'opération en plaçant un $1$ à droite du quotient et en le décalant de $k-1$ rangs vers la gauche lorsque $k-1 \geq 0$, avec $k$ qui représente la différence entre deux positions successives comme on peut le voir sur l'exemple suivant :

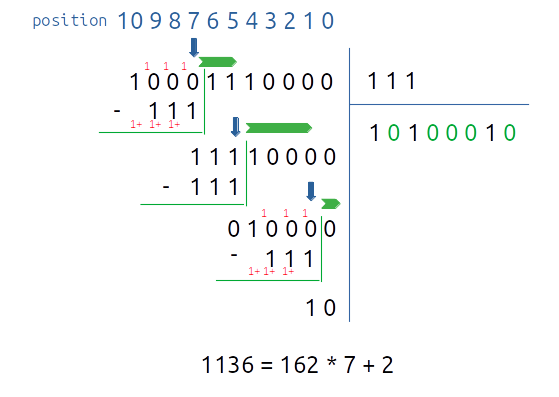
Dans cet exemple, on divise $1136$ par $7$. C'est à partir de la position (ou bit) $7$ que l'on obtient au niveau du dividende, un nombre plus grand que le diviseur, en l'occurrence $1000_2 = 8$. On soustrait alors $7$ à $8$, il nous reste $1$ et on abaisse les chiffres restants du dividende. Etant donné que l'on vient de soustraire une fois $7$ au dividende, on place un $1$ à droite du quotient qui était initialement égal à 0.

On s'intéresse alors au dividende modifié qui est $1111\_0000_2$ et on trouve que l'on peut lui retrancher le diviseur $7 = 111_2$ à partir de la position $5$. On calcule alors $k = 7 - 5 - 1 = 1$, il faut donc décaler le quotient de 1 rang vers la gauche. Le quotient est alors $10_2$ et on place un $1$ à droite du quotient qui devient $101_2$ en raison de la soustraction effectuée.

Le dividende restant est alors $1\_0000_2$. On peut lui retrancher le diviseur à partir de la position $1$. Dans ce cas, $k = 5 - 1 - 1 = 3$. On décale donc le quotient de $3$ rangs vers la gauche, celui-ci devient alors $10\_1000$.

On réalise la soustraction du diviseur au dividende et on place un $1$ à droite du quotient qui est à présent égal à $101\_0001_2$.

Le dividende devient $10_2$, il est inférieur au diviseur donc on arrête la division, mais comme la dernière soustraction a été réalisée en position $1$, il est nécessaire de décaler le quotient d'un rang vers la droite. Finalement le quotient est $1010\_0010_2$, soit $162$ et le reste est de $2$.

On peut en dégager l'algorithme suivant extrait d'une librairie C++ que j'ai écrite :

int pos = greater_or_equal_at(dividend, divisor);
while (pos >= 0)
{
    quotient.shl(1);
    quotient.set_bit(BIT_0, 1);
    sub_at(dividend, divisor, pos);
    int next_pos = greater_or_equal_at(dividend, divisor);
    int shift = pos - next_pos - 1;
    if (shift > 0) quotient.shl(shift);
    pos = next_pos;
}

Ce code repose sur l'utilisation d'une structure de données appelée Bits qui représente une suite de bits par un tableau de caractères, ainsi que sur l'utilisation de deux fonctions :