1. Bases et nombres entiers
1.1. Préambule
Etre informaticien demande de penser d'une certaine manière qui est différente de la manière de penser des mathématiciens : un informaticien d'un bon niveau ne sera pas forcément un mathématicien d'un bon niveau et inversement.
Qu'est ce qui distingue un mathématicien d'un informaticien ?
Par exemple : les mathématiciens travaillent avec la notion d'infini alors que les informaticiens travaillent dans des domaines finis : la taille de la mémoire, la taille du disque dur, le nombre de processeurs ne sont pas infinis.
Un mathématicien peut dire que : quand $n$ tend vers l'infini, $1/n$ tend vers 0 mais ne sera jamais égal à 0. Pour un informaticien, à partir d'une certaine valeur de $n$, il remplacera $1/n$ par 0 car il aura dépassé la capacité de représentation d'un très petit nombre.
Du point de vue de la démarche :
- un mathématicien va démontrer qu'un problème admet ou non des solutions dans telles conditions mais sans donner forcément le moyen d'atteindre ces solutions; la réponse sera de type oui ou non, c'est ce que l'on appelle également un problème de décision
- l'informaticien va s'attacher à trouver :
- une solution
- ou toutes les solutions
- ou tentera de prouver que le problème n'a pas de solution en testant tous les cas possibles, ce qui peut-être très long et demander beaucoup de ressources de calcul
Le fait de savoir, pour un informaticien, que le problème possède ou non une solution peut être d'une grande utilité pour la résolution du problème.
Par exemple, le problème de Ramsey (pour 3 couleurs) consiste à colorier avec trois couleurs un graphe complet de $n$ sommets sans qu'il n'y ait de triangle monochromatique. Un mathématicien peut démontrer :
- que pour $n$ compris entre 3 et 16, ce problème possède des solutions mais sans donner ces solutions
- et qu'il n'en n'admet plus dès que $n ≥ 17$
Au niveau de la machine, l'information est représentée sous forme binaire avec des suites de 0 et de 1. Il est donc primordial de comprendre comment l'information (entiers, réels, texte) est représentée en informatique si on désire raisonner comme un informaticien puisque c'est à partir de cette représentation :
- que l'on peut déduire la limite des calculs possibles que l'on pourra réaliser
- mais également, trouver les traitements les plus efficaces pour résoudre un problème
Pour approfondir...
A titre d'exemple, considérons un traitement qui s'attache à déterminer si un nombre entier est impair ou, en d'autres termes, comment sait-on qu'un nombre entier est impair ?
Facile, me direz-vous, il suffit que ce nombre se termine par l'un des chiffres suivants : 1, 3, 5, 7, 9. Mais comment procéder avec un ordinateur ?
Une première solution consiste à faire ce que font les humains : extraire le chiffre unité du nombre et le comparer à 1, 3, 5, 7 ou 9 :
- CODE
- est_impair_v1.cpp
- #include <iostream>
- using namespace std;
- int main( int argc, char *argv[] ) {
- int x = 123789;
- if (argc > 1) x = atoi( argv[ 1 ] );
- // extraire l'unité
- int u = x % 10;
- // la comparer
- if ((u == 1) || (u == 3) || (u == 5) || (u == 7) || (u == 9)) {
- cout << x << " est impair" << endl;
- } else {
- cout << x << " est pair" << endl;
- }
- return EXIT_SUCCESS;
- }
Voici le code assembleur x86 64 bits qui correspond à ce code :
- CODE
- impair_nasm.asm
- global impair_v3
- section .text
- ; code 64 bits
- ; bool impair_v3(int n)
- ; n => edi
- impair_v3:
- mov eax, edi ; eax <- edi
- xor edx, edx ; edx <- 0
- mov ecx, 10 ; ecx <- 10
- div ecx ; eax <- eax / ecx, (u) edx <- eax % ecx
- mov eax, 1 ; eax <- 1, valeur de retour true
- cmp edx, 1 ; si u == 1 alors sortir de la fonction
- je .end
- cmp edx, 3 ; si u == 3 alors sortir de la fonction
- je .end
- cmp edx, 5 ; si u == 5 alors sortir de la fonction
- je .end
- cmp edx, 7 ; si u == 7 alors sortir de la fonction
- je .end
- cmp edx, 9 ; si u == 9 alors sortir de la fonction
- je .end
- xor eax, eax ; sinon, le nombre est pair on sort avec
- ; la valeur 0 (false)
- .end:
- ret
Un informaticien ne procédera pas ainsi, il sait que la représentation binaire des nombres fait que, si un nombre est impair, il possède son premier bit (bit en position 0) à 1, étant donné que c'est la seule puissance de 2 impaire. Il effectuera donc un ET-binaire avec le nombre et vérifiera que le résultat est égal à 1 ou différent de 0 :
- CODE
- est_impair_v2.cpp
- #include <iostream>
- using namespace std;
- int main( int argc, char *argv[] ) {
- int x = 123789;
- if (argc > 1) x = atoi( argv[ 1 ] );
- if ((x & 1) != 0) {
- cout << x << " est impair" << endl;
- } else {
- cout << x << " est pair" << endl;
- }
- return EXIT_SUCCESS;
- }
Au final, le calcul réalisé par un informaticien est moins coûteux en temps de calcul et moins soumis à certains aléas.
Un test réalisé pour comparer les deux méthodes, et, qui consiste à répéter $50\_000$ fois l'application de l'une des deux fonctions précédentes sur les éléments d'un tableau de $100\_000$ entiers générés dans des conditions particulières, donne les résultats suivants :
| initialisation | méthode 1 | méthode 2 |
| aléatoire | 38.42 | 5.28 |
| nombres unqiuement se terminant par 1 | 12.04 | 5.44 |
| nombres unqiuement se terminant par 3 | 12.23 | 5.41 |
| nombres unqiuement se terminant par 5 | 12.45 | 5.29 |
| nombres unqiuement se terminant par 7 | 12.86 | 5.40 |
| nombres unqiuement se terminant par 9 | 14.81 | 5.50 |
| pairs | 12.46 | 5.49 |
La méthode d'initialisation des éléments du tableau peut être :
- aléatoire : on aura autant de nombres pairs que de nombres impairs
- ne générer que des nombres impairs se terminant par 1, 3, 5, 7 ou 9
- ne générer que des nombres pairs
L'analyse des résultats montre que la méthode 1, traduction de la manière dont procède un humain, est sensible aux données et se révèle toujours moins efficace que la méthode 2.
Dans le cas de données aléatoires (nombres pairs ou impairs sans ordre précis), on note que le temps d'exécution est prohibitif (exorbitant). Cela est dû à la prédiction de branchement qui ne peut déterminer sur quelle valeur de l'unité sortir de la fonction.
Dans ce cas, la méthode 2 est $7,27 = 38,42 / 5,28$ fois plus performante que la méthode 1.
1.2. Représentation d'un nombre dans une base
Tout nombre entier est représenté dans une base $b$, pour laquelle il existe $b$ symboles distincts, sous la forme :
$$ n = ∑↙{i=k}↖l x_i × b^i $$- où chaque $x_i$ est un chiffre compris entre $0$ et $b-1$
- $k$ et $l$ sont des entiers naturels tels que $k ≤ l$, avec :
- $0 ≤ k$, s'il s'agit de nombres entiers
- $k < 0$, s'il sagit de nombres avec une partie décimale
Par exemple, pour la base $10$, appelée base décimale (ou système décimal), il existe $10$ chiffres de $0$ à $9$ et dans cette base le nombre décimal $1876,39$ peut être décomposé en :
$$ 1876,39 = 1000 + 800 + 70 + 6 + 0,3 + 0,09 $$ $$ = 1 × 10^3 + 8 × 10^2 + 7 × 10^1 + 6 × 10^0 + 3 × 10^{-1} + 9 × 10^{-2} $$| $10^3$ | $10^2$ | $10^1$ | $10^0$ | $10^{-1}$ | $10^{-2}$ |
| 1 | 8 | 7 | 6, | 3 | 9 |
Ici $k = -2$ et $l = 3$, il s'agit donc d'un nombre réel et non d'un entier mais on voit que cela fonctionne également dans ce cas de figure.
Nous verrons par la suite (cf. Nombres flottants) que la représentation des nombres décimaux (qui comportent des chiffres après la virgule) dans une autre base engendre des problèmes de précision. Mais pour les nombres entiers, on ne rencontre pas ce problème.
Il existe d'autres bases couramment utilisées comme les bases :
- 12 (duodécimale)
- 60 (sexagésimale) pour les heures, les angles
- d'autres plus anciennes comme la base 20 dite (vicésimale).
En Informatique, on utilise des bases fondées sur des puissances de 2 puisque les circuits électroniques fonctionnent suivant deux états : ouvert / fermé
- le binaire ou base 2
- l'octal ou base 8
- l'hexadécimal ou base 16
Notation
Dans la suite de ce cours, j'ai choisi de mettre en indice de chaque nombre, la base à laquelle il se rapporte. Quand on ne le précise pas, il s'agit par défaut de la base 10.
Dans la suite, afin d'améliorer la lisibilité des nombres, j'utilise également le symbole souligné ( $ \_ $ ) après chaque quartet pour les nombres binaires, chaque triplet pour les nombres décimaux ou chaque paire pour les nombres hexadécimaux :
$$ 11010101010_2 = 110{\_}1010\_1010_2 = 6\_AA_{16} $$$$ = 1706_{10} = 1\_706_{10} = 1\_706 $$
On poura également utiliser la notation suivante :
- b pour le binaire : $1011\_0001_b$ ou $1011\_0001_{2}$
- o pour l'octal : $261_o$ ou $261_{8}$
- d pour le décimal : $177_d$ ou $177_{10}$ ou $177$
- h pour l'héxadécimal : $B1_h$ ou $B1_{16}$
1.2.1. Passer d'une base b au système décimal
Pour convertir un nombre écrit dans une base $b$ vers le système décimal, il suffit de traduire chaque chiffre en son équivalent décimal et le multiplier par la puissance de $b$ correspondante.
Par exemple avec la base $8$, le nombre à virgule $432,5_8$, correspond à :
$$ n = \; 4 × 8^2 \; + \; 3 × 8^1 \; + \; 2 × 8^0 \; + \; 5 × 8^{-1} $$ $$ n = \; 4 × 64 \; + \; 3 × 8 \; + \; 2 × 1 \; + \; 5 × 0,125 $$ $$ n = \; 256 \;+\; 24 \;+\; 2 \;+\; 0,625 \;=\; 282,625_{10} $$Exercice 1.1
Convertir les nombres suivants en base 10 :
- $1101_2$ et $1\_1101_2$
- $222_8$
Pour l'hexadécimal, on utilise des lettres pour représenter les chiffres de A (=10) à F (=15) :
1.2.2. Passer du système décimal à une base b
Pour convertir un nombre entier en base 10 dans une base $b$, il suffit de le diviser successivement par $b$ :
- tant que le quotient de la division est supérieur ou égal à $b$, on continue de diviser
- lorsque le quotient est inférieur à $b$, on s'arrête et on relit le nombre en partant de la dernière division
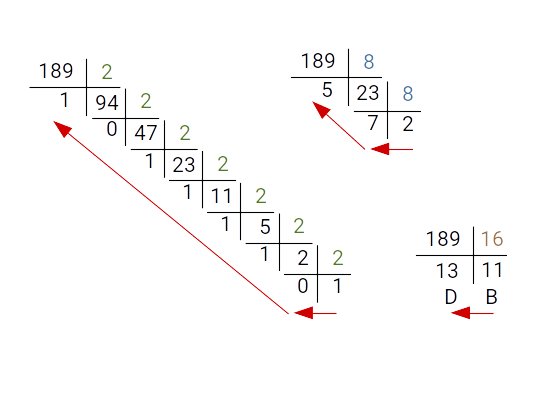
Dans l'exemple précédent, $189_{10} = 1011\_1101_2 = 275_8 = BD_{16} $.
Pour approfondir...
Un autre manière de procéder consiste à écrire le nombre à convertir $x$ dans un tableau à deux lignes et plusieurs colonnes. On place $x$ dans la colonne la plus à droite possible :
- en dessous de $x$, on place le modulo de $x$ par $b$ (noté $x \; % \; b$ en informatique, ou encore $x\; \text"mod" \; b$). Pour rappel, le modulo est le reste de la division entière de $x$ par $b$
- puis dans la case de gauche sur la même ligne que $x$, on place $((x - (x \; % \; b)) / b)$
Par exemple pour traduire $189$ en base $2$ :
| x | 0 | 1 | 2 | 5 | 11 | 23 | 47 | 94 | 189 |
| x mod b | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
On lit alors le nombre de la gauche vers la droite : $1011\_1101_2$.
1.3. Les entiers naturels
On s'intéresse à la représentation des nombres positifs ou nuls, c'est à dire $ℕ$.
1.3.1. Le binaire
En Informatique, l'information est représentée en binaire car les composants électroniques de base qui forment les ordinateurs sont des transistors qui agissent comme des interrupteurs qui laissent ou empêchent le courant électrique de passer.
Voici une petite vidéo expliquant les unités en binaire bit, byte, kb, etc.
Pour approfondir...
les transistors agissent soit comme des amplificateurs de courant, soit comme des interrupteurs.
L'information au sein de la mémoire centrale est implantée sous forme d'un condensateur qui contient (ou pas) une charge de courant, et ce condensateur est lié à un transistor qui en gère l'accès.
Si le condensateur est chargé, il représente un 1, sinon il représente un 0.
La mémoire centrale est appelée DRAM ou Dynamic Random Access Memory, soit en français Mémoire Dynamique à Accès Aléatoire.
Le terme aléatoire est mal choisi. Il signifie qu'on peut accéder à tout emplacement de la mémoire. Le terme Access signifie que l'on peut accéder à la mémoire en lecture ou en écriture. On peut donc y lire une donnée ou y écrire une donnée en spécifiant l'adresse où l'on désire lire ou écrire.
L'unité la plus petite que l'on puisse représenter en binaire est le bit (BInary digiT). Le bit peut contenir soit la valeur 0, soit la valeur 1. Mais le microprocesseur manipule les données par groupe de 8, 16, 32, 64, 128, 256 voire 512 bits en les chargeant dans ses registres qui sont en quelques sorte des variables temporaires utilisées pour réaliser toutes sortes d'opérations (addition, multiplication, décalage, etc) :
- les registres généraux al ou ah sont des registres 8 bits
- le registre général ax=(ah,al) est un registre 16 bits
- le registre général eax est un registre 32 bits
- le registre général rax est un registre 64 bits
- les registres vectoriels xmm0 à xmm15 sont des registres 128 bits (technologie SSE = SIMD Streaming Extensions)
- les registres vectoriels ymm0 à ymm15 sont des registres 256 bits (technologie AVX = Advanced Vector eXtensions)
- les registres vectoriels zmm0 à zmm31 sont des registres 512 bits (technologie AVX512)
On nomme des quantités de plusieurs bits bien définies comme suit :
- le quartet (nibble) est un groupe de 4 bits consécutifs
- l'octet (byte) est un groupe de 8 bits consécutifs
- le mot (word) représente 16 bits consécutifs
- le double mot (double word) représente 32 bits consécutifs
- le quatre ou quadruple mot (quad word) représente 64 bits consécutifs
- enfin, le double quad word représente 128 bits
On fait parfois référence, dans la représentation binaire, au :
- bit le plus significatif (most significant bit)
- bit le moins significatif (least significant bit)
Cependant, tout dépend de ce à quoi on fait référence :
- si on parle d'une représentation sur $N$ bits alors
- le bit le plus significatif est le dernier bit, c'est-à-dire le bit d'indice $N-1$ puisqu'on numérote à partir de 0, il correspond, pour les valeurs signées au bit de signe (0 = positif, 1 = négatif)
- le bit le moins significatif est le bit d'indice 0
- si on parle d'un nombre binaire sur $N$ bits alors
- bit le plus significatif (most significant bit), qui est le bit de valeur 1, d'indice le plus grand : instruction assembleur BSR pour Bit Scan Reverse)
- bit le moins significatif (least significant bit), qui est le bit de valeur 1, d'indice le plus faible : instruction assembleur BSF pour Bit Scan Forward)
Par exemple pour le nombre binaire suivant codé sur 8 bits $0101\_0100_2 = 84_{10}$, le bit le plus significatif est le bit d'indice 6 et le moins significatif, le bit 2. On commence la notation à partir de l'indice 0 :
| Bit N° | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| N = | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
S'il s'agit d'une représentation sur 32 bits par exemple, on parlera du bit le plus significatif comme étant le bit de position 31 et le bit le moins significatif comme étant celui à la position 0.
Pour représenter un nombre entier naturel en Informatique, il suffit simplement de le coder en base 2.
Attention, il est nécessaire de fixer la taille de la représentation, c'est à dire le nombre de bits consécutifs que l'on utilise pour coder le nombre, soit, en général : 8, 16, 32 ou 64 bits.
Par exemple avec 8 bits, on peut représenter $2^8$ valeurs différentes :
- de $0000\_0000_2$ à $1111\_1111_2$
- c'est à dire de 0 à 255 (en décimal), ou encore, de 0 à $2^8 - 1$
- soit 256 ($= 2^8$) valeurs différentes
Voici les plus grands nombres que l'on peut représenter en fonction du nombre de bits choisis pour la représentation :
| Nbr Bits | Valeur Min | Valeur Max | Approx. |
| 8 | $0$ | $2^8-1=255$ | |
| 16 | $0$ | $2^{16}-1 = 65\_535$ | |
| 32 | $0$ | $2^{32}-1 = 4\_294\_967\_295$ | $≈ 4,3 × 10^9$ |
| 64 | $0$ | $2^{64}-1 = 18\_446\_744\_073\_709\_551\_615$ | $ ≈ 18,44 × 10^{18}$ |
Il est également intéressant de connaître les multiples du kilo octet puisqu'ils définissent la taille des fichiers et des espaces de stockage :
| Puissance | Préfixe | Puissance | Préfixe | |
| $2^{10}$ | kilo | $2^{50}$ | Peta | |
| $2^{20}$ | Mega | $2^{60}$ | Exa | |
| $2^{30}$ | Giga | $2^{70}$ | Zetta | |
| $2^{40}$ | Tera | $2^{80}$ | Yotta |
Ainsi 1 Go (1 Giga octets) représente $2^{30} = (2^{10})^3 = 1024^3 = 1\_073\_741\_824$ octets, soit un peu plus d'un milliard d'octets.
La petite histoire suivante permet de se rappeler l'ordre des puissances : le K correspond au kilo, le M au méga, etc :
Karla Mangeait
de Grandes Tortillas
et du Pain de Élote,
Zen, sur son Yacht
Exercice 1.2
Vous pouvez essayer de l'adapter de manière à prendre pour chaque mot, les deux ou trois premières lettres du préfixe.
Par exemple avec le site suivant l'internaute.fr, on peut prendre Kiki ou Kilo pour commencer la phrase.
Par exemple : un KILO de MEGAlos GIGottait TERminant de PETArader EXAltés par le ZETétique YOgi
1.3.1.a addition en binaire
L'addition en binaire est similaire à l'addition en système décimal. Il existe 5 cas à traiter pour l'addition de deux nombres :
- $0_2 + 0_2 = 0_2$
- $0_2 + 1_2 = 1_2$
- $1_2 + 0_2 = 1_2$
- $1_2 + 1_2 = 10_2$, on abaisse le $0$ et on génère une retenue de $1$
- enfin le dernier cas correspond à une retenue en entrée de $1$, dès lors $1_2 + 1_2 + 1_2 = 11_2$, on abaisse le premier $1$ et on génère une retenue en sortie de $1$
Considérons une représentation des nombres sur 8 bits, pour le calcul de $1101\_1010_2 + 1110\_1111_2$.
Dans ce cas on ne garde que les 8 premiers bits du résultats :
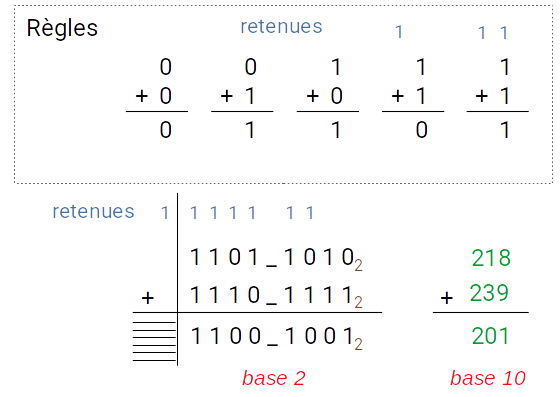
Le résultat est-il correct ?
Oui si le résultat de l'addition reste dans l'intervalle de représentation.
Si on est en dehors de l'intervalle de représentation on obtiendra un résultat faux mais qui est égal au modulo du nombre de valeurs de l'intervalle.
- ici, on effectue le calcul $218 + 239 = 457$
- $218$ et $239$ sont bien dans l'intervalle $[0,255]$
- cependant $457$ n'est pas dans cet intervalle, le résultat que l'on obtient est donc faux
- $457$ modulo $256$ est égal à $201 = 1100\_1001_2$, c'est pour cela que l'on obtient $201$ comme résultat final
Exercice 1.3
Réaliser les additions suivantes après avoir traduit les nombres en binaire sur 8 bits, vérifier que le résultat est correct et expliquer pourquoi.
- $21 + 64$
- $127 + 6$
- $240 + 27$
1.3.1.b Multiplication en binaire
La multiplication en binaire est similaire à celle en décimal.
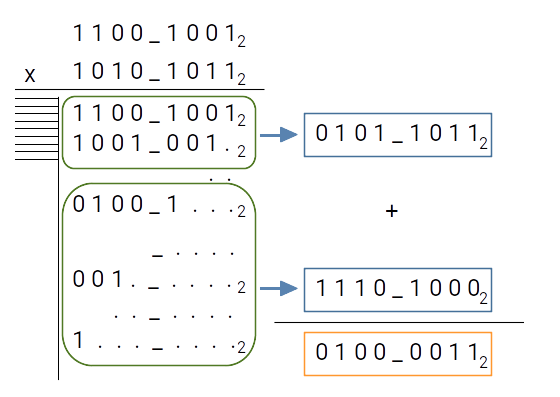
La seule difficulté réside dans les additions que l'on peut réaliser soit en totalité, soit par étapes (deux à deux) : Il est important de noter que si on prend une représentation sur $n$ bits, on ne garde que les $n$ premiers bits de la somme.
On applique les mêmes règles que précédemment pour interpréter le résultat final, si le résultat de la multiplication reste dans l'intervalle de représentation alors le calcul est juste, sinon il faudra prendre le modulo du nombre de valeurs de l'intervalle de représentation.
Dans le calcul ci-dessus on réalise le produit $201 × 171 = 34\_371$ :
- $201$ et $171$ sont bien dans l'intervalle $[0,255]$
- cependant le résultat $34\_371$ n'est pas dans cet intervalle, le résultat que l'on obtient est donc faux
- $34\_371$ modulo $256$ est égal à $67$ car $34\_371 = 134 × 256 + 67$, c'est pour cela que l'on obtient $67$ comme résultat final
1.3.1.c Décalage à droite, décalage à gauche
Cas particulier de la multiplication par une puissance de 2:
- multiplier un nombre binaire par $2^n$ consiste à ajouter $n$ chiffres $0$ à sa droite.
- diviser un nombre binaire par $2^n$ consiste à retirer $n$ chiffres à sa droite (que ce soit des $0$ ou des $1$).
Le vérifier en multipliant 5, écrit en binaire, par 2, 4 et 8.
Ajouter un $0$ à droite d'un nombre, ou multiplier ce nombre par $2$, correspond à faire un décalage à gauche de ce nombre, c'est l'opération SHL (SHift Left) en assembleur. En C/C++, il s'agit de l'opérateur <<.
Supprimer un chiffre ($0$ ou $1$) à droite d'un nombre, ou diviser ce nombre par $2$, correspond à faire un décalage à droite de ce nombre, c'est l'opération SHR (SHift Right) en assembleur. En C/C++, il s'agit de l'opérateur >>.
Attention, en C ou C++, on n'écrit pas $2^i$ mais 1 << i, c'est à dire la valeur 1 que l'on décale de $i$ rangs vers la gauche.
- $2^0 = 1 $ ↔ 1 << 0
- $2^1 = 10_2 = 2 $ ↔ 1 << 1
- $2^2 = 100_2 = 4 $ ↔ 1 << 2
- etc
- CODE
- decalages.cpp
- #include <iostream>
- #include <cmath> // pour pow(x,y)
- /* ------------------------------------------------------------------
- QUOI
- Fonction principale
- ------------------------------------------------------------------ */
- int main() {
- // Définition de 1 Mo
- int un_Mo = 1 << 20;
- std::cout << "1 Mo = " << un_Mo << " octets" << std::endl;
- int v = 137;
- // multiplication par 8=2^3 de v
- int v_mul_8 = v << 3;
- std::cout << v << " * 8 = " << v_mul_8 << std::endl;
- // division par 2 = 2^1 de v
- int v_div_2 = v >> 1;
- std::cout << v << " / 2 = " << v_div_2 << std::endl;
- // utilisation des décalages
- std::cout << "-------------" << std::endl;
- for (int i = 0; i < 6; ++i) {
- std::cout << "2^" << i << " = " << (1 << i) << std::endl;
- }
- // utilisation de la fonction (power) pow(x,y)
- // dont la signature est double pow(double x, double y);
- std::cout << "-------------" << std::endl;
- for (int i = 0; i < 6; ++i) {
- std::cout << "2^" << i << " = " << pow( 2, i ) << std::endl;
- }
- return EXIT_SUCCESS;
- }
Le résultat de l'exécution du programme précédent donne :
1 Mo = 1048576 octets
137 * 8 = 1096
137 / 2 = 68
-------------
2^0 = 1
2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16
2^5 = 32
-------------
2^0 = 1
2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16
2^5 = 32
1.3.2. L'octal

Tableau de contrôle de l'UNIVAC 1105 36 bits, 1958
(Source Michel Talbot)
Sur les premiers ordinateurs l'octal était très souvent utilisé. Sur l'image ci-dessus les registres sont de 36 bits soit 12 fois 3 bits.
La base 8 est utilisée pour représenter des octets comme par exemple des caractères mais elle est en général peu usitée. On la retrouve lors de l'utilisation de commandes Unix (cf. cours Bases de l'Informatique 2) comme chmod qui change les droits d'accès à un fichier ou la commande tr qui permet de transposer ou d'éliminer des caractères dans un fichier ou un flux de données. Voici, par exemple, deux commandes Unix qui utilisent l'octal :
richer@universe:~$ chmod 644 fichier
richer@universe:~$ tr ':' '\012' < fichier
La première ligne donne au propriétaire les droits de modification et lecture, aux membres du groupe et aux autres uniquement les droits de lecture sur le fichier.
La seconde permet de remplacer le caractère ':' par un saut de ligne car $12_{8} = 10$ ce qui correspond au caractère '\n' (Line Feed, voir chaînes de caractères). Il faut noter que le nombre commence par un $0$ qui indique qu'il faut lire la valeur en octal.
1.3.3. L'hexadécimal
La base $16$ ou base hexadécimale permet de représenter des adresses ou des nombres utilisant plusieurs bits comme les double et quadruple mots. Ainsi un double mot qui occupe $32$ bits, soit $32$ chiffres en binaire, utilise seulement $8$ chiffres hexadécimaux.
On utilise également la base 16 pour le codage des couleurs en HTML/CSS en donnant les trois composantes Rouge/Vert/Bleu avec une valeur variant de 0 à 255 :
- rouge : #FF0000
- vert : #00FF00
- bleu : #0000FF
- magenta : #FF00FF
- jaune : #FFFF00
- orange : #FF8800
Dans la base $16$ on utilise les chiffres $0$ à $9$ ainsi que des lettres pour représenter les chiffres supérieurs ou égaux à 10 en partant de $A$ qui vaut $10$ pour aller jusqu'à $F$ qui vaut $15$ en décimal :
| Chiffre | 0 | 1 | .. | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Représentation | 0 | 1 | .. | 9 | A | B | C | D | E | F |
On remarquera qu'en langage C ou en langage assembleur, on peut écrire les nombres hexadécimaux en les préfixant avec 0x, on écrira donc 0xA2F8.
Le passage du binaire à l'hexadécimal est simple puisqu'un quartet (4 bits consécutifs) correspond à un chiffre hexadécimal.
$$ FA91_{16} = 1111\_1010\_1001\_0001_2 $$1.4. Les entiers relatifs
On s'intéresse à présent à la représentation des entiers relatifs, c'est à dire $ℤ$.
Pour représenter les nombres négatifs, on utilise la notation dite binaire en complément à deux.
| Nbr bits | Valeur Min | Valeur Max | NB Valeurs |
| 8 | $-128$ | $127$ | $256$ |
| 16 | $-32\_768$ | $32\_767$ | $65\_536$ |
| 32 | $-2\_147\_483\_648$ | $2\_147\_483\_647$ | $4\_294\_967\_296$ |
| 64 | $-9\_223\_372\_036\_854\_775\_808$ | $9\_223\_372\_036\_854\_775\_807$ | $18\_446\_744\_073\_709\_551\_616$ |
Pour ce type de notation, il faut, comme précédemment, fixer la taille de la représentation en nombre de bits. Par exemple, si on choisit 8 bits, on ne pourra représenter que des valeurs entre -128 et +127. Si on désire représenter la valeur -199, cela n'est pas possible avec 8 bits, il faudra passer à 9 bits.
Pour représenter un nombre en notation binaire en complément à deux, on procède ainsi :
- si le nombre est positif on procède comme avec les entiers naturels
- si le nombre est négatif, on doit effectuer trois étapes de transformation :
- on prend la valeur absolue du nombre et on la code sur le nombre de bits choisis pour la représentation
- on complémente la valeur obtenue, c'est à dire qu'on change les 0 en 1 et inversement
- on ajoute 1 au résultat précédent
Exercice 1.4
On se place dans le cadre de la notation binaire en complément à deux sur 8 bits, c'est à dire que la taille de la représentation est de 8 bits.
Coder les nombres suivants dans cette notation :
- $-1$
- $-2$
- $-127$
- $-128$
- $-129$, que remarque t-on pour ce cas particulier ?
Notes :
- vous remarquerez également que quand on code -x sur 8 bits, le codage correspond à 256-x.
- si un calcul est en dehors de l'intervalle de recherche, on trouvera un résultat modulo 256
1.5. Addition et multiplication
On procède avec les mêmes règles que les entiers naturels.
Exercice 1.5
On se place dans le cadre de la notation binaire en complément à deux sur 8 bits.
Effectuer les calculs suivants dans cette notation et dire s'ils sont corrects ou non :
- $-1 + 3$
- $-65 + -2$
- $-65 + -64$
Exercice 1.6
On se place dans le cadre de la notation binaire en complément à deux sur 8 bits.
Effectuer les calculs suivants dans cette notation et dire s'ils sont corrects ou non :
- $-1 × 3$
- $-65 × -2$, on est en dehors de l'intervalle $[-128,+127]$, on doit donc obtenir $-(256-130) = -126$
- $-65 × -3$, on est en dehors de l'intervalle $[-128,+127]$, on doit donc obtenir $-(256-195) = -61$
- $-65 × -65$, on est en dehors de l'intervalle $[-128,+127]$, on doit donc obtenir $4225 = 256 × 16 + 129$, donc $256-129=-127$
- $-13 × -6$
Exercice 1.7
Calculer la somme 15 + 15 + 15 en représentant les nombres en binaire.
Vous pouvez procéder en réalisant une première somme de 15 avec 15, puis ajouter le résultat au dernier 15.
Ou alors, vous pouvez réaliser l'addition des trois valeurs en même temps et propager les retenues.