2. Nombres flottants

2.1. Introduction

Les nombres réels ne sont pas représentables en totalité en informatique en raison de la forme et de la taille de la représentation utilisée. Nous allons voir que nous ne pouvons en coder qu'une partie. On utilise une notation spécifique issue de la norme IEEE 754. Les nombres qui résultent de cette transformation sont appelés nombres flottants ou nombres à virgule flottante.

En informatique, on note les nombres flottants sous la forme suivante :

zéro : $0.0$, ou parfois $0$ comme pour les entiers, la conversion sera réalisée par le compilateur

$3.14159265$, la virgule est remplacée par le point, il s'agit de la notation anglo-saxonne

$1.89e-3 = 0.00189$, le caractère 'e' ou 'E' représente l'exposant, c'est à dire $10^n$, avec ici $n=-3$

Dans la norme IEEE 754, il existe une modélisation qui utilise 32 bits, appelée également simple précision. La double précision utilise quant à elle 64 bits.

Nous allons étudier la simple précision qui correspond au type float du langage C. Elle consiste à représenter un nombre $N$ en base 10 sous une forme binaire :

Si $N = 0$ alors on aura 32 bits à la valeur 0, par contre si $N ≠ 0$ :

$$ N_{10} = M × 2^E $$

où la mantisse $M$ est une suite de $0$ et de $1$ qui représente le codage binaire de $N$, et $E$ est l'exposant associé à $N$.

1 bit de signe $S$, le bit de poids fort (bit 31) qui vaut 0 pour un nombre positif et 1 pour un nombre négatif
8 bits pour coder l'exposant décalé (ou biaisé) $E_d$, car par convention on lui ajoute 127
23 bits pour coder la mantisse tronquée $M_t$, elle est dite tronquée car on a supprimé le premier bit du nombre qui vaut forcément 1 pour tout nombre différent de 0

Signe	Exposant Décalé								Mantisse Tronquée
1	1	0	0	0	1	0	0	1	0	0	0	0	0	0	0	0	1	1	1	0	1	0	0	0	0	0	0	0	0	0	0
1 bit	← 8 bits →								← 23 bits →
C				4				8				0				7				4				0				0
-1027.625

Le nombre réel $N$ qui correspond au nombre flottant s'exprime alors sous la forme :

$$ N = (-1)^S × 1,M_t × 2^(E_d - 127) $$

On peut alors coder des nombres entre ± $3,4027 × 10^{38}$ et ± $1,1754 × 10^{-38}$.

Par exemple :

si $S=1$, $M_t = 0$ et $E_d = 127$, alors on a $n = -1$.
si $S=0$, $M_t=11_2$ et $E_d = 128$, alors on a $n = 1,11_2 × 2^(128-127) = 11,1_2 = 2 + 1 + 0,5 = 3,5$
si $S=0$, $M_t=0$ et $E_d = 0$, alors il s'agit de $+0$
si $S=1$, $M_t=0$ et $E_d = 0$, alors il s'agit de $-0$

Vous pouvez utiliser l'IEEE 754 Converter pour représenter des nombres flottants.

2.1.1. Coder un réel en flottant

Comment coder un nombre réel au format IEEE 754 ? Prenons l'exemple de la représentation en simple précision sur 32 bits du codage de $n = -1027,625$ ci dessous.

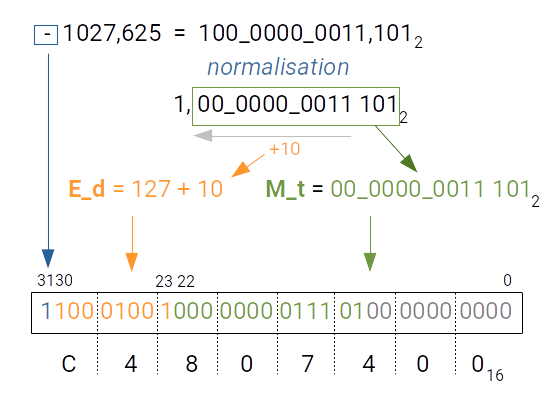
On procède comme suit :

il s'agit d'un nombre négatif donc $S = 1$
on code la partie entière en valeur absolue : $$1027_{10} = 1024_{10} + 2_{10} + 1_{10} = 2^{10} + 2^{1} + 2^{0} = 100\_0000\_0011_{2}$$
on code la partie décimale en utilisant des puissances de 2 négatives : $$0,625 = 0,5 + 0, 125 = 2^{-1} + 2^{-3}$$

La mantisse qui regroupe partie entière et décimale est alors:

$$M = 100\_0000\_0011,101_{2}$$

Pour obtenir la mantisse tronquée et l'exposant décalé, il suffit de déplacer la virgule vers la gauche derrière le premier 1 qui compose la mantisse, on parle alors de normalisation du nombre à représenter :

$$1,0000\_0000\_1110\_1_{2}$$

Par conséquent, on a déplacé la virgule de 10 rangs vers la gauche (cf. image ci-dessus) ce qui correspond à l'exposant $E = 10$.

la mantisse tronquée est alors égale à la mantisse à laquelle on a enlevé le premier 1 devant la virgule, on obtient donc $M_t = 0000\_0000\_1110\_1_{2}$
l'exposant décalé est égal, par convention en 32 bits, à $127 + E$, dans notre cas $E = 10$, donc : $$E_d = 127 + 10 = 137_{10} = 1000\_1001_{2}$$

On remplit alors chacun des champs du nombre flottant et on complète la mantisse tronquée par des zéros à droite. Au final on obtient une valeur sur 32 bits que l'on exprime généralement en hexadécimal pour plus de lisibilité. On obtient donc $C4\_80\_74\_00_{16}$.

S	Exposant Décalé								Mantisse Tronquée
1	1	0	0	0	1	0	0	1	0	0	0	0	0	0	0	0	1	1	1	0	1	0	0	0	0	0	0	0	0	0	0
C				4				8				0				7				4				0				0

2.1.2. Pourquoi ajouter 127 à l'exposant ?

The eight-bit exponent uses excess 127 notation. What this means is that the exponent is represented in the field by a number 127 greater than its value. Why? Because it lets us use an integer comparison to tell if one floating point number is larger than another, so long as both are the same sign.

Soit $x$ et $y$ deux nombres décimaux et $x'$ et $y'$ leurs représentations à virgule flottante interprétée sous forme d'entier non signé.

en fonction du signe, si $x <= y$ alors $x' <= y'$ ou alors $x' >= y'$

Exemples de valeurs
Nombre $x$	Hexadécimal $x'$
-100000.000000	c7c35000
-1000.000000	c47a0000
-100.000000	c2c80000
-10.000000	c1200000
-1.000000	bf800000
-0.000010	b727c5ac
0.000000	0
0.000010	3727c5ac
1.000000	3f800000
10.000000	41200000
100.000000	42c80000
1000.000000	447a0000
100000.000000	47c35000

Par exemple, si on compare :

deux nombres de même signe :
- deux nombres négatifs : si $x < y$ alors $x' > y'$
- deux nombres positifs : si $x < y$ alors $x' < y'$
deux nombres de signes différents : si $x < y$ alors $x' > y'$

2.1.3. Comment coder la partie décimale ?

Imaginons que nous ayons à coder $0,4$, comment procéder ?

Il existe un algorithme simple pour réaliser le codage :

Cette méthode consiste à multiplier la partie décimale par $2$ jusqu'à obtenir 0 quand cela est possible ou, si on ne s'arrête pas, à obtenir assez de chiffres pour remplir la mantisse.

A chaque étape on garde le chiffre de la partie entière $z$ et on réitère le processus sur $(2x -z)$.

Vous pouvez tester avec un exemple :

Exercice 2.1

Essayer de convertir $0,3$, $0,6$ ou $0,9$ en utilisant cet algorithme.

Que remarquez vous ?

2.1.4. IEEE 754 64 bits et les autres précisions

Pour approfondir...

Pour la modélisation en 64 bits, dite double précision, on utilise :

toujours 1 bit pour le signe comme en 32 bits
11 bits pour l'exposant, on ajoute 1023 pour obtenir l'exposant décalé
52 bits pour la mantisse tronquée

Enfin il existe :

la demi précision qui occupe 16 bits
la simple précision étendue (40 bits), la double précision étendue (80 bits)
la quadruple précision qui utilise 128 bits

Caractéristiques des représentations IEEE 754
Précision :	demi	simple	double	quadruple
Signe (bits)	$1$	$1$	$1$	$1$
Exposant (bits)	$5$	$8$	$11$	$15$
Mantisse (bits)	$11$	$23$	$52$	$113$
Plus petit nombre	$± 6,103 10^{-5}$	$± 1,175 10^{-38}$	$± 2,225 10^{-308}$	$± 3.362 10^{-4932}$
Plus grand nombre	$± 65504$	$± 3,402 10^{38}$	$± 1,797 10^{308}$	$± 1.189 10^{4932}$
Décimales	$3$	$7$	$16$	$34$

2.1.5. Erreurs de précision

Lorsque l'on utilise la représentation IEEE 754, on rencontre deux problèmes liés à la précision des valeurs codées :

Comme on utilise que des puissances de 2 négatives qui se terminent par 5, on ne peut donc coder la plupart des nombres décimaux qu'en utilisant une combinaison de puissances de 2 négatives et cela engendre des erreurs de précision :

Vous pouvez utiliser le formulaire suivant pour calculer la somme des valeurs cochées ou chercher une valeur approchée d'une valeur spécifique comprise entre 0 et 1,0. Vous pouvez essayer avec 0,3 ou 0,33 par exemple.

n	Sel.	2^n
-1		0.50000000000000000000000
-2		0.25000000000000000000000
-3		0.12500000000000000000000
-4		0.06250000000000000000000
-5		0.03125000000000000000000
-6		0.01562500000000000000000
-7		0.00781250000000000000000
-8		0.00390625000000000000000
-9		0.00195312500000000000000
-10		0.00097656250000000000000
-11		0.00048828125000000000000
-12		0.00024414062500000000000
-13		0.00012207031250000000000
-14		0.00006103515625000000000
-15		0.00003051757812500000000
-16		0.00001525878906250000000
-17		0.00000762939453125000000
-18		0.00000381469726562500000
-19		0.00000190734863281250000
-20		0.00000095367431640625000
-21		0.00000047683715820312500
-22		0.00000023841857910156250
-23		0.00000011920928955078125
-24		0.00000005860464477539062

L'autre problème lié à la précision provient du fait que la taille de la mantisse peut être trop petite pour représenter certains nombres qui comportent beaucoup de chiffres, notamment en 32 bits, car on dispose de 7 chiffres significatifs.

Pour approfondir...

C'est pour cela que le coprocesseur arithmétique, que l'on appelle également FPU (Floating Point Unit) qui réalise les opérations sur les nombres flottants, utilise un codage sur 80 bits afin de minimiser les erreurs de précision.

Un processeur contient plusieurs coeurs de calcul et chaque coeur possède une ou plusieurs FPU.

2.1.5.a Exemple

On peut voir sur le listing suivant un exemple de code très simple qui réalise la différence entre des valeurs flottantes proches.

CODE
code c++

#include <iostream>
#include <iomanip>
#include <cmath>
 
// Définition de variables globales
float v1 = 1.2;
float v2 = 1.3;
float v3 = 1.3001;
float v4 = 1.3001001;
 
/* ------------------------------------------------------------------
    QUOI
       Fonction principale
       
   ------------------------------------------------------------------ */
int main() {
 
    float diff_v1_v2 = v1 - v2;
    float diff_v2_v3 = v2 - v3;
 
    std::cout << setprecision(10);
 
    std::cout << "v1-v2 = " << diff_v1_v2 << std::endl;
    std::cout << "v2-v3 = " << diff_v2_v3 << std::endl;
 
    // Comparaison de valeurs flottantes
    float diff_abs = fabs(v3 - v4);
    std::cout << "|v3-v4| = " << diff_abs << std::endl;
 
    if (diff_abs < 1E-6) 
        std::cout << "v3 = v4" << std::endl;
    else
        std::cout << "v3 != v4" << std::endl;
    return 0;
}
 

Cependant, le résultat de l'exécution ne correspond pas à ce que nous devrions obtenir :

v1-v2 = -0.09999990463     ! et non -0.1
v2-v3 = -0.0001000165939   ! et non -0.0001
|v3-v4| = 1.192092896e-07  ! et non  0.0000001
v3 = v4

la différence v1 - v2 devrait être égale à $-0.1$
et celle de v2 - v3 devrait être de $-0.0001$

Cela est dû au fait qu'il est impossible de coder exactement certaines valeurs comme nous l'avons expérimenté pour représenter $0,3$.

Le problème lié aux erreurs de précision implique que pour comparer deux valeurs en virgule flottante on ne peut pas utiliser l'opérateur d'égalité (==) du langage C comme on le ferait pour des entiers, il est nécessaire d'utiliser la valeur absolue de la différence des deux valeurs (lignes 27 et 30 du listing précédent) et de vérifier que cette différence est bien inférieure à un $ε$ donné.

On doit donc écrire :

// permet de comparer deux float
if (fabs(x1 - x2) < 1e-6) {
    // égalité
}

au lieu de :

// ne permet pas de comparer deux float
if (x1 == x2) {
    // égalité
}

Si on utilise une précision plus grande de 64 bits, c'est à dire un double en langage C, on obtient un résultat qui correspond à un calcul exact :

v1-v2 = -0.1
v2-v3 = -0.0001
|v3-v4| = 1.000000001e-07
v3 = v4

Néanmoins, on obtiendra les mêmes erreurs de précision dès lors que les nombres à traiter possèdent un nombre de chiffres après la virgule important qui dépasse la capacité de représentation des nombres en double précision.

2.1.5.b GNU Multi precision Library

Pour approfondir...

Si on désire faire des calculs exacts, il existe une librairie dédiée appelée GMP pour The GNU Multiple Precision Arithmetic Library.

Pour installer la librairie GMP procéder comme suit sous Ubuntu :

sudo apt install build-essential m4
tar -xf gmp-6.3.0.tar.xz 
cd gmp-6.3.0/
./configure --build=`config.guess` --enable-cxx
make -j4
sudo make install
sudo ldconfig

α) Pour les entiers

CODE
gmp_integer_example.cpp

// compiler avec g++ -o gmp_integer_example.exe gmp_integer_example.cpp -O3 -lgmp
#include <gmp.h>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;
 
// fonction qui transforme une chaine de la forme 1289347884
// en 1_289_347_884
 
string separateur(const string& input, char separator = '_') {
    string result;
    int count = 0;
 
    // Iterate the string in reverse order
    for (int i = input.size() - 1; i >= 0; --i) {
        result.push_back(input[i]);
        count++;
 
        // Insert separator every 3 digits, but not after the last group
        if (count == 3 && i != 0) {
            result.push_back(separator);
            count = 0;
        }
    }
 
    // Reverse the result string back to correct order
    std::reverse(result.begin(), result.end());
    return result;
}
 
ostream& operator<<(ostream& out, mpz_t& z) {
    char* str = mpz_get_str(nullptr, 10, z);  
    out << separateur( str );  // Output the string to the stream
    free(str);
    return out;
}
 
int main() {
    mpz_t a, b;
    
    mpz_init(a);
    mpz_init(b);
    
    // calculer 2^64 en multipliant a=1 par b=2 64 fois
    mpz_set_ui(a, 1);
    mpz_set_ui(b, 2);
    
    for (int i = 1; i <= 64; ++i) {
        mpz_mul(a, a, b);
    }
    
    cout << "2^64 = " << a << endl;
    
    // utiliser la fonction puissance pour calculer 2^128
    mpz_ui_pow_ui(a, 2, 128);
    cout << "2^128 = " << a << endl;
    
    // utiliser la fonction puissance pour calculer 2^32
    mpz_ui_pow_ui(a, 2, 32);
    cout << "2^32 = " << a << endl;
    
    
    mpz_clear(a);
    mpz_clear(b);
    
    return EXIT_SUCCESS;
}
 

L'affichage donnera :

2^64 = 18_446_744_073_709_551_616
2^128 = 340_282_366_920_938_463_463_374_607_431_768_211_456
2^32 = 4_294_967_296

CODE
gmp_factorial.cpp

#include <iostream>
#include <gmpxx.h>
 
int main() {
    // Version utilisant la syntaxe C++
    // ainsi que l'opérateur '*'
    
    // Declare an arbitrary precision integer class
    mpz_class factorial = 1;
 
    // Loop from 1 to 50, multiplying 'factorial' by the current number
    for (int i = 1; i <= 50; i++) {
        factorial *= i;
    }
 
    // Print the result. The overloaded << operator handles printing
    std::cout << "The factorial of 50 is:\n" << factorial << std::endl;
 
    return 0;
}
 
 

richer@solaris:~$ g++ -o gmp_factorial.exe gmp_factorial.cpp -lgmpxx -lgmp
richer@solaris:~$ ./gmp_factorial.exe 
The factorial of 50 is:
30414093201713378043612608166064768844377641568960512000000000000

β) Pour les flottants

Calcul de Pi avec la série de Leibniz :

CODE
gmp_float_example.cpp

#include <iostream>
#include <iomanip>
#include <gmpxx.h>
 
/**
 * Calcul de Pi, exemple donné par Gemini de Google
 * Utilisation de la série de Leibniz
 *
 *  Pi/4 = 1 -1/3 + 1/5 -1/7 + 1/9 + ...
 */
int main() {
    mpf_set_default_prec(200);
 
    mpf_class pi = 0;
    mpf_class term;
 
    long long num_terms = 100000000;
 
    for (long long n = 0; n < num_terms; ++n) {
        if (n % 2 == 0) {
            term = 1;
        } else {
            term = -1;
        }
 
        // Convertir explicitement le résultat en long int avant de construire mpf_class
        mpf_class denominator = static_cast<long int>(2 * n + 1);
        term /= denominator;
 
        pi += term;
    }
 
    pi *= 4;
 
    std::cout << "Pi avec la série de Leibniz (" << num_terms << " termes) est :\n";
    std::cout << std::fixed << std::setprecision(50) << pi << std::endl;
 
    return 0;
}
 

L'affichage donnera :

Pi avec la série de Leibniz (100000000 termes) est :
3.14159264358979323846264363327950288419713814937511

Page de Jean-Michel Richer

2. Nombres flottants

2.1. Introduction

2.1.1. Coder un réel en flottant

2.1.2. Pourquoi ajouter 127 à l'exposant ?

2.1.3. Comment coder la partie décimale ?

2.1.4. IEEE 754 64 bits et les autres précisions

2.1.5. Erreurs de précision

2.1.5.a Exemple

2.1.5.b GNU Multi precision Library

α) Pour les entiers

β) Pour les flottants