Paralèlisme : cours
Liste des travaux pratiques / dirigés
- td 1 : Produit de matrices
- td 2 : Réduction
- td 3 : Scan
- td 4 : Tri
- td 5 : Jeu de la vie
- td 6 : Courbes de julia
- td 7 : Résolution d'équation
- td 8 : easy MPI
- td 9 : Problème du cavalier
7. Equation
7.1. Objectif
On s'intéresse à la parallèlisation de la résolution d'une équation linéaire.
On dispose de 7 variables entières prenant leurs valeurs entre 0 et $N$ (inclus) et on cherche toutes les solutions de l'équation :
$$ ∑↙{i=1}↖7 i × x_i = N $$On demande de mettre en place une résolution simple qui consiste, lorsque toutes les variables sont instanciées, à vérifier que la somme pondérée des valeurs est égale ou non à $N$.
Proposer les méthodes de résolution suivantes :
- méthode 1 : sans parallélisation
- méthode 2 : parallèle en utilisant OpenMP sur les valeurs de la première variable à instancier
- méthode 3 : amélioration de la méthode 2 avec variable locale pour compter le nombre de solutions
On effectuera les tests de performance pour $N = 26$ :
- temps de référence en séquentiel (mono-thread, méthode 1)
- temps en parallèle avec 2 à 26 threads par pas de 2 (méthode 2)
7.2. Résultats
Par exemple, sur AMD Ryzen 5 9600X, on obtient les temps suivants :
./equation.exe -m 1 -n 26
Nombre de solutions : 1_009
Résolution séquentielle : 23.89 s
Résolution en parallèle
==========================
Threads | Meth.2 | Meth.3
==========================
2 | 12.06 | 12.76
4 | 6.17 | 6.64
6 | 4.58 | 4.91
8 | 5.07 | 5.37
10 | 4.57 | 4.72
12 | 4.70 | 4.98
14 | 4.70 | 4.99
16 | 4.69 | 5.49
18 | 4.69 | 4.96
20 | 4.69 | 4.99
22 | 4.70 | 4.97
24 | 4.71 | 5.50
26 | 4.70 | 4.96Les calculs selon la métrique de Karp-Flatt ($e$) indiquent que le nombre de coeurs devrait être de 2 ou de 4 pour atteindre une parallélisation optimale. L'augmentation de $e$ signifie que la perte d'efficacité est due à l'augmentation du surcoût de parallélisation (comme la synchronisation, les opérations atomiques).
Temps de référence (1 thread): 23.8900 s
================================================================================
Analyse de la performance de l'application
Fraction parallèle (Par) utilisée pour Amdahl: 0.98
================================================================================
Threads | Temps (s) | Accélération | Amdahl | Karp-Flatt
--------------------------------------------------------------------------------
1 | 23.8900 | 1.0000 | 1.0000 | -1.0000
2 | 12.0600 | 1.9809 | 1.9608 | 0.0096
4 | 6.1700 | 3.8720 | 3.7736 | 0.0110
6 | 4.5800 | 5.2162 | 5.4545 | 0.0301
8 | 5.0700 | 4.7120 | 7.0175 | 0.0997
10 | 4.5700 | 5.2276 | 8.4746 | 0.1014
12 | 4.7000 | 5.0830 | 9.8361 | 0.1237
14 | 4.7000 | 5.0830 | 11.1111 | 0.1349
16 | 4.6900 | 5.0938 | 12.3077 | 0.1427
18 | 4.6900 | 5.0938 | 13.4328 | 0.1490
20 | 4.6900 | 5.0938 | 14.4928 | 0.1540
22 | 4.7000 | 5.0830 | 15.4930 | 0.1585
24 | 4.7100 | 5.0722 | 16.4384 | 0.1622
26 | 4.7000 | 5.0830 | 17.3333 | 0.1646
On peut également calculer le % de diminution du temps de calcul en fonction du nombre de threads :
Méthode 2
K | % | Detla%
1 ----- -----
2 -49.52 -49.52
4 -74.17 -24.65
6 -80.83 -6.66
8 -78.78 2.05
10 -80.87 -2.09
12 -80.33 0.54
14 -80.33 0.00
16 -80.37 -0.04
18 -80.37 0.00
20 -80.37 0.00
22 -80.33 0.04
24 -80.28 0.04
26 -80.33 -0.04
Lorsque l'on passe de 4 à 6 threads on ne gagne plus que 6% et ensuite on ne progresse plus. On peut donc en conclure que 4, voire 6 threads sont suffisants dans les conditions données de résolution du problème.
7.3. Modification de la fonction d'évaluation
Si on modifie la fonction d'évaluation de l'équation par une somme non pondérée :
$$ ∑↙{i=1}↖7 x_i = N $$On obtient beaucoup plus de solutions : 906_192 pour $N = 26$.
La méthode 3 se montre alors plus performante que la méthode 2. Pouvez-vous expliquer pourquoi ?
./equation.exe -m 1 -n 26
Nombre de solutions : 906_192
Résolution séquentielle : 18.15 s
Résolution en parallèle
==========================
Threads | Meth.2 | Meth.3
==========================
2 | 9.60 | 6.51
4 | 5.69 | 3.36
6 | 4.28 | 2.53
8 | 4.23 | 2.71
10 | 3.69 | 2.37
12 | 3.88 | 2.51
14 | 3.90 | 2.48
16 | 3.87 | 2.48
18 | 3.92 | 2.48
20 | 3.91 | 2.50
22 | 3.86 | 2.52
24 | 3.89 | 2.58
26 | 3.92 | 2.49Temps de référence (1 thread): 18.1500 s
Méthode 3
================================================================================
Analyse de la performance de l'application
Fraction parallèle (Par) utilisée pour Amdahl: 0.98
================================================================================
Threads | Temps (s) | Accélération | Amdahl | Karp-Flatt
--------------------------------------------------------------------------------
1 | 18.1500 | 1.0000 | 1.0000 | -1.0000
2 | 6.5100 | 2.7880 | 1.9608 | -0.2826
4 | 3.3600 | 5.4018 | 3.7736 | -0.0865
6 | 2.5300 | 7.1739 | 5.4545 | -0.0327
8 | 2.7100 | 6.6974 | 7.0175 | 0.0278
10 | 2.3700 | 7.6582 | 8.4746 | 0.0340
12 | 2.5100 | 7.2311 | 9.8361 | 0.0600
14 | 2.4800 | 7.3185 | 11.1111 | 0.0702
16 | 2.4800 | 7.3185 | 12.3077 | 0.0791
18 | 2.4800 | 7.3185 | 13.4328 | 0.0859
20 | 2.5000 | 7.2600 | 14.4928 | 0.0924
22 | 2.5200 | 7.2024 | 15.4930 | 0.0978
24 | 2.5800 | 7.0349 | 16.4384 | 0.1049
26 | 2.4900 | 7.2892 | 17.3333 | 0.1027
Méthode 3
K | % | Detla%
1 ----- -----
2 -64.13 -64.13
4 -81.49 -17.36
6 -86.06 -4.57
8 -85.07 0.99
10 -86.94 -1.87
12 -86.17 0.77
14 -86.34 -0.17
16 -86.34 0.00
18 -86.34 0.00
20 -86.23 0.11
22 -86.12 0.11
24 -85.79 0.33
26 -86.28 -0.50
7.4. Version MPI
Reprendre le code de la version séquentielle et l'adapter pour créer un programme MPI. Le maître détermine quelles valeurs dans l'intervalle $[0,N]$ doivent être traitées par chacun des processus esclaves. Le maître réalisera également une partie des calculs.
Par exemple si N=26, on a la répartition suivante :
q=6 # 27 / 4 = 6
r=3 # 27 % 4 = 3
0: 0 to 7 soit de 0 à 6, donc 7 éléments
1: 7 to 14 soit de 7 à 13, donc 7 éléments
2: 14 to 21 soit de 14 à 20, donc 7 éléments
3: 21 to 27 soit de 21 à 26, soit 6 élémentsDans ce cas, la répartition du nombre de solutions est la suivante :
time mpirun -n 4 ./equation_mpi.exe -n 26
master : 709
slave 1: 235
slave 2: 58
slave 3: 7
nbr_solutions=1009
real 0m5,807s
user 0m22,144s
sys 0m0,030s
7.4.1. Tests de performance sur une machine
Tester le programme avec 2, 4, 6, 8, 10 processus :
time mpirun -oversubscribe -n 8 ./equation_mpi.exe -n 26
q=3
r=3
0: 0 to 4
1: 4 to 8
2: 8 to 12
3: 12 to 15
4: 15 to 18
5: 18 to 21
6: 21 to 24
7: 24 to 27
master : 487
slave 1: 274
slave 2: 143
slave 3: 56
slave 4: 28
slave 5: 14
slave 6: 5
slave 7: 2
nbr_solutions=1009
real 0m4,828s
user 0m28,966s
sys 0m0,100sOn obtient par exemple sur AMD Ryzen 9600X, les temps suivants :
Temps de référence (1 thread): 21.6300 s
================================================================================
Analyse de la performance de l'application
Fraction parallèle (Par) utilisée pour Amdahl: 0.99
================================================================================
Threads | Temps (s) | Accélération | Amdahl | Karp-Flatt
--------------------------------------------------------------------------------
1 | 21.6300 | 1.0000 | 1.0000 | -1.0000
2 | 11.3700 | 1.9024 | 1.9802 | 0.0513
4 | 5.8400 | 3.7038 | 3.8835 | 0.0267
6 | 4.4500 | 4.8607 | 5.7143 | 0.0469
8 | 4.4500 | 4.8607 | 7.4766 | 0.0923
10 | 4.4800 | 4.8281 | 9.1743 | 0.1190
================================================================================
1 ----- -----
2 -47.43 -47.43
4 -73.00 -25.57
6 -79.43 -6.43
8 -79.43 0.00
10 -79.29 0.147.4.2. Tests de performance sur deux machines
On réalise les tests sur deux machines :
- AMD Ryzen 5 9600X à 5,4 GHz, 12 threads
- AMD Ryzen 5 5600G à 4,4 GHz, 12 threads
On répartit équitablement les processus sur les deux machines en allant de 2 à 24 threads par pas de 2.
On observe des résultats fluctuants en raison du fait que les machines disposent de 6 coeurs + 6 HT, notamment pour un nombre de threads compris entre 20 et 24. Dans cet intervalle le temps minimum obtenu est associé à 20, 22 ou 24 threads.
Voici un exemple d'exécution :
Temps de référence (1 thread): 23.8900 s
================================================================================
Analyse de la performance de l'application
Fraction parallèle (Par) utilisée pour Amdahl: 0.99
================================================================================
Threads | Temps (s) | Accélération | Amdahl | Karp-Flatt
--------------------------------------------------------------------------------
1 | 23.8900 | 1.0000 | 1.0000 | -1.0000
2 | 20.7600 | 1.1508 | 1.9802 | 0.7380
4 | 12.7300 | 1.8767 | 3.8835 | 0.3771
6 | 8.0200 | 2.9788 | 5.7143 | 0.2028
8 | 6.1600 | 3.8782 | 7.4766 | 0.1518
10 | 6.1000 | 3.9164 | 9.1743 | 0.1726
12 | 4.6200 | 5.1710 | 10.8108 | 0.1201
14 | 5.9200 | 4.0355 | 12.3894 | 0.1899
16 | 5.5300 | 4.3201 | 13.9130 | 0.1802
18 | 5.0900 | 4.6935 | 15.3846 | 0.1668
20 | 4.2600 | 5.6080 | 16.8067 | 0.1351
22 | 3.6800 | 6.4918 | 18.1818 | 0.1138
24 | 5.7500 | 4.1548 | 19.5122 | 0.2077
================================================================================
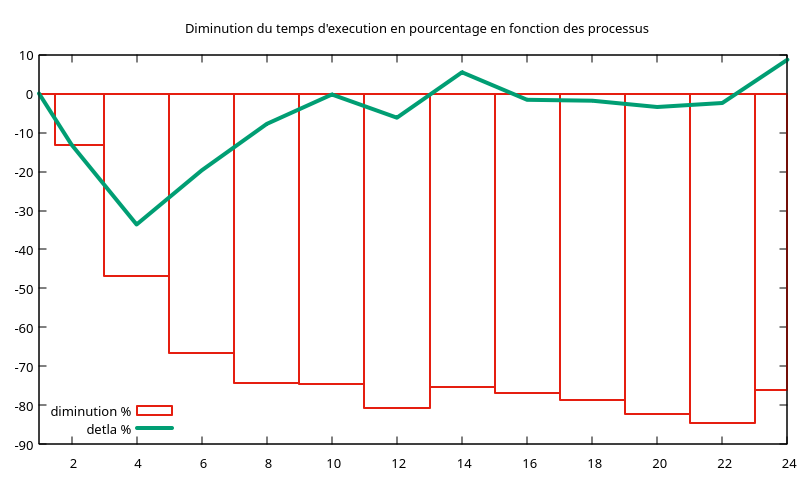
1 ----- -----
2 -13.10 -13.10
4 -46.71 -33.61
6 -66.43 -19.72
8 -74.22 -7.79
10 -74.47 -0.25
12 -80.66 -6.20
14 -75.22 5.44
16 -76.85 -1.63
18 -78.69 -1.84
20 -82.17 -3.47
22 -84.60 -2.43
24 -75.93 8.66
Pourquoi le temps pour 2 processus est-il de presque 21 secondes alors qu'il est de 11 secondes si on exécute MPI sur une machine ?