Parallélisme : cours

Liste des travaux pratiques / dirigés

1. Produit de Matrices

1.1. Travail demandé

On s'intéresse à la parallélisation du produit matriciel. On rapelle que le produit de deux matrices $A(n × p)$ par $B(p × q)$ est une matrice $C(n × q)$ telle que : $$ C_i^j = ∑↙{k=1}↖{p} A_i^k × B_k^j $$

Ce qui se traduit en informatique par le code C++ suivant :

CODE
matrix_product

template<class T>
class Matrix {
public:
    int rows, cols, size;
    T *data;
    
    Matrix() {
        rows = cols = size = 0;
        data = nullptr;
    }
    
    Matrix(int _rows, int _cols) {
        rows = _rows;
        cols = _cols;
        size = _rows * _cols;
        data = new T [ size ];
    }
    
    ...
    
    T& operator()(int i, int j) {
        return data[ i * cols + j ];
    }
    
};
 
template<class T>
void product( Matrix<T>& a, Matrix<T>& b, Matrix<T>& c) {
    c.resize( a.rows, b.cols );
    for (int i = 0; i < a.rows; ++i) {
        for (int j = 0; j < b.cols; ++j) {
            T sum = (T) 0;
            for (int k = 0; k < a.cols; ++k) {
                sum += a(i,k) * b(k,j);
            }
            c(i,j) = sum;
        }
    }
}
 

Ecrire un programme C++ (matrix_product.exe) qui permet de réaliser le produit de deux matrices carrées de double $A$ et $B$. La méthode de calcul choisie ainsi que la dimension des matrices (qui par défaut est de 1024) seront passées en arguments du programme (penser à utiliser getopt).

Les méthodes à implanter sont les suivantes :

méthode 1 : produit classique
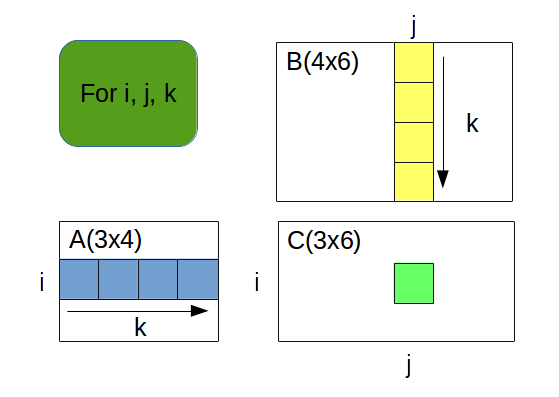
méthode 2 : version OpenMP de la méthode 1 avec parallélisation de la boucle la plus externe (i)
méthode 3 : version OpenMP de la méthode 1 avec parallélisation de la boucle (j)
méthode 4 : version OpenMP de la méthode 1 avec parallélisation des boucles i et j (collapse)
méthode 5 : modification de la méthode 4 avec inversion des boucles j et k
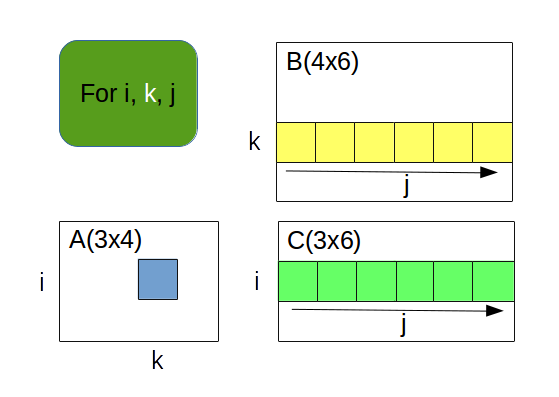
méthode 6 : version OpenMP de la méthode 5 avec parallélisation de la boucle la plus externe (i)
méthode 7 : version OpenMP de la méthode 5 avec parallélisation de la boucle (k)
méthode 8 : version OpenMP de la méthode 5 avec parallélisation des boucles i et k (collapse)

Attention, l'une de ces méthodes ne donne pas de résultat correct.

1.2. Performance et graphiques

Validité et performance

Réaliser un script bash (test_matrix_product_validity.sh) qui permet de vérifier si chaque méthode donne un résultat correct du calcul. On affichera par exemple le coefficient C[0,0] de la matrice qui servira de valeur de référence.

Réaliser un script bash (test_matrix_product_performance.sh) qui permet de calculer les temps de calculs avec les différentes versions valides et de les comparer.

On génèrera des graphiques grâce à gnuplot (ou octave) pour comparer l'efficacité du calcul des méthodes avec différentes dimensions de matrices notamment 512, 1024, 2048, 4096.

On pourra utiliser la commande /usr/bin/time -f "%e;%E;%U" bin/matrix_product.exe paramètres pour obtenir les temps de calcul.

Les fichiers de données seront de la forme matrix_1.gpd, matrix_2.gpd, etc (d'extension .gpd pour GnuPlot Data) et contiendront les temps d'exécution de chaque méthode pour les dimensions 512, 1024 et 2048 :

512 0.34
1024 4.03
2048 49.96
3092 66.66
4096 438.22

P-Core et E-Core

Attention concernant les P-Cores (Performance) et E-Cores (Efficiency) sur les microprocesseurs Intel. Il faut déjà commencer par utiliser les threads des P-Cores. Voici un exemple concernant un Core i7-12700 :

richer@jupiter:~/parallelisme\$ lscpu --all --extended
CPU NODE SOCKET CORE L1d:L1i:L2:L3 ONLINE    MAXMHZ   MINMHZ       MHZ
 0    0      0    0 0:0:0:0          oui 4800,0000 800,0000  963,9030
 1    0      0    0 0:0:0:0          oui 4800,0000 800,0000  800,0000
 2    0      0    1 4:4:1:0          oui 4800,0000 800,0000  919,5970
 3    0      0    1 4:4:1:0          oui 4800,0000 800,0000  800,0000
 4    0      0    2 8:8:2:0          oui 4800,0000 800,0000  800,0000
 5    0      0    2 8:8:2:0          oui 4800,0000 800,0000  800,0000
 6    0      0    3 12:12:3:0        oui 4800,0000 800,0000  800,0000
 7    0      0    3 12:12:3:0        oui 4800,0000 800,0000  800,0000
 8    0      0    4 16:16:4:0        oui 4900,0000 800,0000  970,0560
 9    0      0    4 16:16:4:0        oui 4900,0000 800,0000  975,6290
10    0      0    5 20:20:5:0        oui 4800,0000 800,0000  799,5960
11    0      0    5 20:20:5:0        oui 4800,0000 800,0000  800,0000
12    0      0    6 24:24:6:0        oui 4900,0000 800,0000  800,6420
13    0      0    6 24:24:6:0        oui 4900,0000 800,0000  800,0000
14    0      0    7 28:28:7:0        oui 4800,0000 800,0000  948,9300
15    0      0    7 28:28:7:0        oui 4800,0000 800,0000  883,2450
16    0      0    8 36:36:9:0        oui 3600,0000 800,0000  985,2560
17    0      0    9 37:37:9:0        oui 3600,0000 800,0000  800,0000
18    0      0   10 38:38:9:0        oui 3600,0000 800,0000  800,0000
19    0      0   11 39:39:9:0        oui 3600,0000 800,0000 1173,8900

On peut noter que les cores numérotés :

0,2,4,6,8,10,12,14 sont des cores Performance (fréquence max de 4,8 Ghz et Hyperthreading)
1,3,5,7,9,11,13,15 sont la partie HyperThreading des cores précédents
16,17,18,19 sont les cores Efficiency (Fréquence max de 3,6 Ghz et pas d'Hyperthreading)

Il faudra donc utiliser taskset afin d'affecter le travail à des P-Cores. Par exemple pour 4 threads :

taskset -c 0,2,4,6 ./macommande.exe parametres

1.2.1. GNUPlot

Voici un exemple de script gnuplot (matrix.gps) qui utilise le fichier de palette suivant palette.pal pour afficher les graphiques obtenus :

# fichier matrix.gps
set term pdfcairo enhanced size 6in,5in color font 'Helvetica,12'
set output "matrix.pdf"
# use of palette to have different line colors
load 'palette.pal'
# define grid
set style line 102 lc rgb '#808080' lt 0 lw 1
set grid back ls 102

set key below
set title "matrix product"
set xlabel "dimension of matrix"
set ylabel "Time in seconds"
set xtics rotate by -90
plot "matrix_1.gpd" using 1:2 with lines ls 1 title "m1", "matrix_2.gpd" using 1:2 with lines ls 2 title "m2", "matrix_3.gpd" using 1:2 with lines ls 3 title "m3", "matrix_4.gpd" using 1:2 with lines ls 4 title "m4", "matrix_5.gpd" using 1:2 with lines ls 5 title "m5", "matrix_6.gpd" using 1:2 with lines ls 6 title "m6"

1.2.2. GNU Octave


% Load the data from the text file
data = load('matrix.gps');

% Separate the data into X and Y
X = data(:, 1);  % First column is dimension 
Y = data(:, 2);  % Second column is execution time

% Plot the data
figure;
plot(X, Y, '-o');  % Plot with line and points
xlabel('X values');
ylabel('Y values');
title('Plot of X vs Y');
grid on;  % Add grid for better visualization

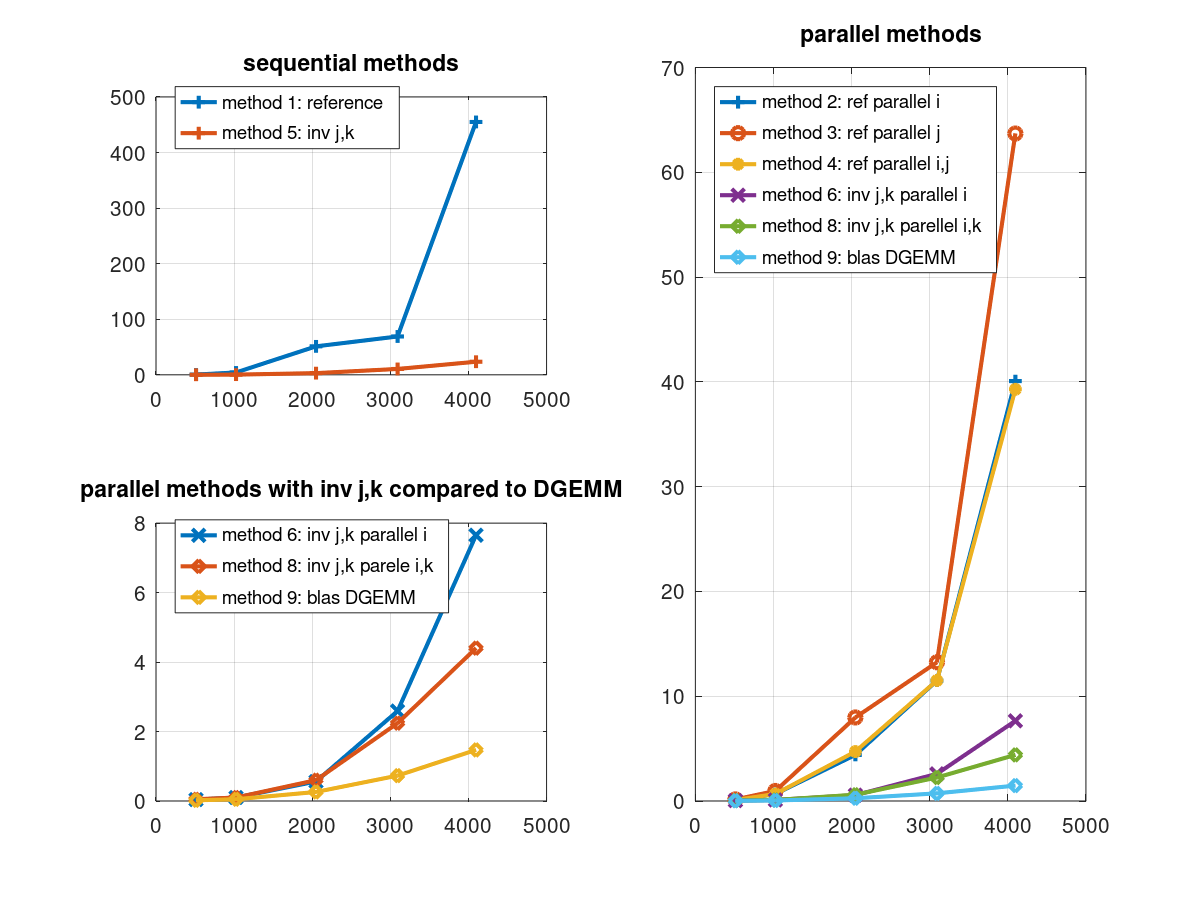
Exemple de graphique généré avec GNU Octave

BLAS

Utiliser la librairie BLAS (Basic Linear Algebra Subprograms) pour faire le produit de matrices notamment le sous-prorgamme DGEMM. BLAS est une librairie de sous-programmes optimisés pour calcul matriciel :

BLAS niveau 1 : scalar, vector et vector-vector
BLAS niveau 2 : matrix-vector
BLAS niveau 3 : matrix-matrix

Voir la BLAS Reference Card.

Sous Ubuntu, installer les packages :

pour BLAS : libblas3 libblas-dev et réaliser l'édition de liens avec -lblas
pour OpenBLAS : libopenblas-base libopenblas-dev et réaliser l'édition de liens avec -lopenblas

Voici à présent un exemple de code pour l'appel afin d'effectuer un produit de matrices avec double DGEMM (Double GEneral Matrix Matrix) :

$$ C ← α . op(A) × op(B) + β . C $$

où $α$ et $β$ sont des réels et $op$ est soit l'identité, la transposée ou la transposée conjuguée.

CODE
blas_matrix_product.cpp

#include <iostream>
#include <numeric>
using namespace std;
#include <cblas.h>
#include <xmmintrin.h>
 
/*
extern "C" void cblas_dgemm(const enum CBLAS_ORDER Order, const enum CBLAS_TRANSPOSE TransA,
                 const enum CBLAS_TRANSPOSE TransB, const int M, const int N,
                 const int K, const double alpha, const double *A,
                 const int lda, const double *B, const int ldb,
                 const double beta, double *C, const int ldc);
 */
int DIM = 1000;
double *A;
double *B;
double *C;
                 
int main(int argc, char *argv[]) {
    char TRANS = 'N';
    double alpha = 1.0;
    double beta = 0.0;
 
    srand(19702013);
    
    if (argc > 1) {
        DIM = atoi(argv[1]);
    }
    
    int size = DIM*DIM;
    
    // allocate
    A = static_cast<double *>(_mm_malloc(size * sizeof(double), 16));
    B = static_cast<double *>(_mm_malloc(size * sizeof(double), 16));
    C = static_cast<double *>(_mm_malloc(size * sizeof(double), 16));
    
    // fill
    for (int i=0; i<size; ++i) {
        A[i] = (rand() % 131) * 0.01;
        B[i] = (rand() % 131) * 0.01;
    }
    
    cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans, DIM, DIM, DIM, 
        alpha, A, DIM, B, DIM, beta, C, DIM);
 
    // check result
    double sum = accumulate(&C[0], &C[size], 0.0);
    
    cout << "sum = " << sum << endl;
    
    _mm_free(A);
    _mm_free(B);
    _mm_free(C);
    return 0;
}
 

Analyse Amdahl et Karp-Flatt

Soit les résultats suivants :

; size K time
4096 1 288,53
4096 2 158,09
4096 4 80,73
4096 6 56,04
4096 8 50,05
4096 10 36,23
4096 12 29,77
4096 14 28,27
4096 16 28,42
4096 18 29,23
4096 20 28,26
4096 22 27,75
4096 24 29,54

Calculez l'accélération ainsi que la métrique de Karp-Flatt afin de déterminer quel est le nombre de cores optimal pour réaliser le produit de matrices 4096x4096 sur un AMD Ryzen 5600G :

Calculez l'accélération théorique ainsi que les temps d'exécution théoriques (d'après la loi de Amdahl), si on passe 99% du temps dans la partie parallèle.

Page de Jean-Michel Richer