Cette page fait partie du cours de polytech PeiP1 et 2 Bio

10. Mise en pratique : SVM

10.1. Introduction

Les SVM (Support Vector Machines) où Machines à Vecteur de Support sont en fait un classifieur linéaire dit à large marge.

On rappelle que le classifieur permet de séparer (classer) des données lorsque l'on connaît déjà les classes existantes. On parle alors de classification Supervisée par opposition à la classification Non Supervisée pour laquelle on ne connaît pas le nombre de classes.

• classification Supervisée : on connaît le nombre de classes
• classification Non Supervisée : on ne connaît pas le nombre de classes

10.2. Le cadre théorique

Voici deux liens concernant des éléments théoriques liés aux SVM :

• Cours
• Vidéo Youtube

L'utilisation d'un kernel (qui est une fonction) permet de modifier l'espace initial des données et de les transposer dans un espace d'ordre supérieur :

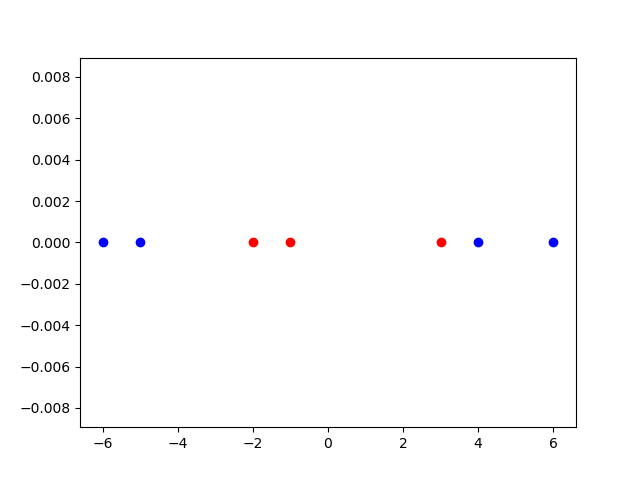
SVM Linéaire sans Kernel

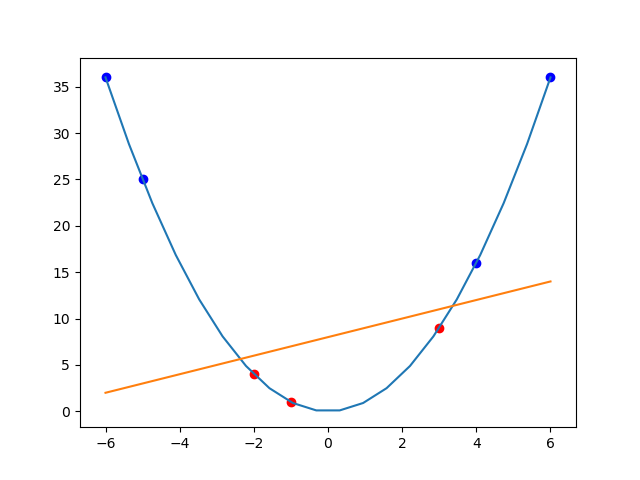
SVM Linéaire avec Kernel $x^2$

Le problème des SVM et qu'elles dépendent de beaucoup de paramètres et que la recherche des meilleurs paramètres (ceux qui donnent la meilleure prédiction) peut demander beaucoup de temps. On pourra, afin de les rechercher, utiliser la classe GridSearchCV du paquet sklearn.model_selection.

10.3. Application aux Iris de Fisher

10.3.1. Apprentissage et validation

On essaye d'appliquer le classifieur SVM aux iris de Fisher afin de prédire, à partir des données des sépales ou pétales, à quelle espèce appartient l'iris : Setosa, Versicolor, Virginica .

Dans le cadre de l'apprentissage, on a tendance à séparer les données en deux sous-ensembles :

• l'ensemble d'apprentissage $(X_a, y_a)$ qui permet de calculer une SVM
• l'ensemble de validation $(X_v, y_v)$

On se trouve confronté ici à un dilemme du même type que celui ci:

• soit on utilise cette technique de séparation des données en sous-ensembles d'apprentissage et de validation, mais on risque de sous-apprendre par rapport à l'ensemble des données, c'est à dire de ne pas prendre en compte des données essentielles à l'apprentissage
• soit on prend toutes les données et on risque de nous reprocher d'avoir une connaissance parfaite de nos données, ce que l'on peut qualifier de sur apprentissage

Tout ceci n'est qu'une affaire de point de vue car dans le cas où on prend la totalité des données, il est évident que de nouvelles données viendront s'ajouter par la suite qui confirmeront ou infirmeront le modèle d'apprentissage.

10.3.2. Résolution

Pour résoudre notre problèmen on utilise la classe SVC (C-Support Vector Classification) du paquet svm.

classifier = SVC(C=0.006, kernel='rbf', gamma='scale')

classifier = SVC(C=1.0, kernel='poly', gamma='auto', degree=7)

10.4. Mise en application