Ce site est en cours de reconstruction certains liens peuvent ne pas fonctionner ou certaines images peuvent ne pas s'afficher.
Cette page fait partie du cours de polytech PeiP1 et 2 Bio
5. Mise en pratique : Graphiques
5.1. Introduction
Dans ce TP nous allons apprendre à générer des graphiques avec Python.
Pour cela nous utiliserons le package matplotlib.
5.2. Tracé d'une fonction (plot)
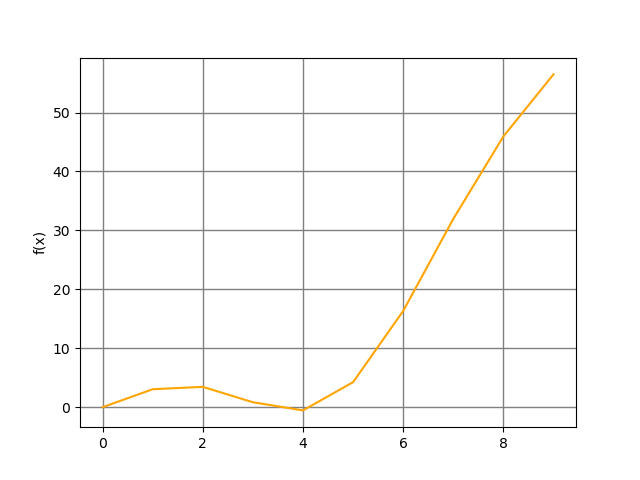
On désire tracer une fonction réelle. On utilise pour cela la fonction plot.
On peut également utiliser la fonction savefig afin de sauvegarder un graphique.
5.2.1. Sans numpy
Voici une première version sans numpy. On utilise la fonction sinus et il est donc nécessaire de faire appel au module math (plot_function_without_numpy.py) :
Warning: file_get_contents(polytech/plot_function_without_numpy.py): Failed to open stream: No such file or directory in /home/jeanmichel.richer/public_html/ez_web.php on line 418
Afficher le code polytech/plot_function_without_numpy.py
On calcule les valeurs pour x (x_values) puis celles de y(y_values) et enfin on dessine la courbe en utilisant ces valeurs.
5.2.2. Avec numpy
Voici une seconde version avec numpy ce qui permet de simplifier la génération des valeurs à la fois pour x et pour y. On notera l'utilisation de np.sin(x) au lieu de math.sin(x) dans le calcul de la fonction $f$ (plot_function_with_numpy.py) :
Warning: file_get_contents(polytech/plot_function_with_numpy.py): Failed to open stream: No such file or directory in /home/jeanmichel.richer/public_html/ez_web.php on line 418
Afficher le code polytech/plot_function_with_numpy.py
On remarquera que l'on utilise la fonction linspace de numpy afin de générer des valeurs dans l'intervalle [0,10].
Exercice 5.1
Afficher le graphique de la fonction :
$$
f1(x) = (√|x| - 3) × x
$$
Exercice 5.2
Afficher sur le même graphique les fonctions :
$$\{\table
f1(x) = x;
f2(x) = x × \log(x);
f3(x) = x × x;
$$
5.3. Données en barres (bar, barh)
Il est parfois nécessaire de modéliser les données sous forme graphique et les graphes qui utilisent des barres permettent de rendre compte d'une donnée numérique associée à une catégorie.
A titre d'exemple, considérons que nous avons interrogé 75 personnes et que nous leur avons demandé quel langage de programmation elles utilisent le plus souvent. Voici les résultats de ce sondage :
- C++ : 20
- Ruby : 10
- Python : 30 personnes
- Php : 15 personnes
5.3.1. Barres verticales (bar)
On peut représenter ces données sous forme de barres verticales ce qui permet tout de suite de voir quel langage est le plus utilisé et quel langage est le moins utilisé, est-ce qu'un langage se démarque des autres, etc.
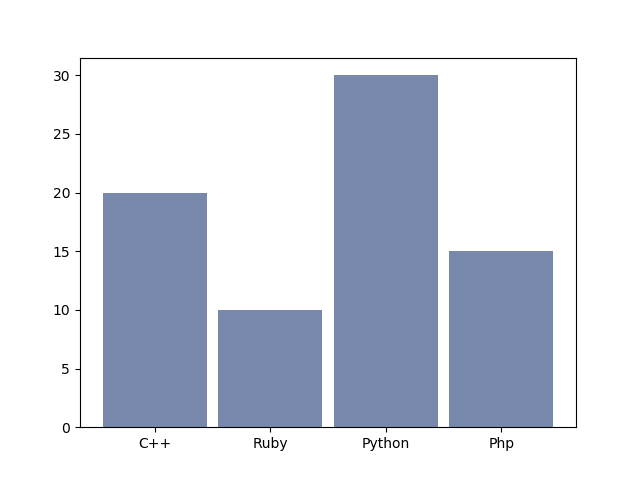
Voici le code (plot_bar_chart.py) :
Warning: file_get_contents(polytech/plot_bar_chart.py): Failed to open stream: No such file or directory in /home/jeanmichel.richer/public_html/ez_web.php on line 418
Afficher le code polytech/plot_bar_chart.py
5.3.2. Barres horizontales (barh)
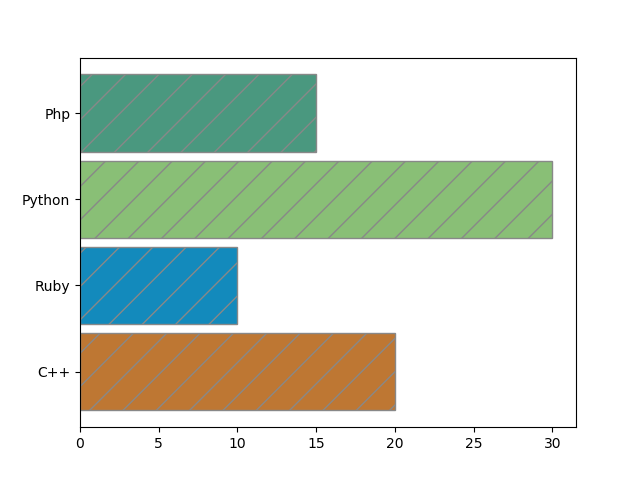
On peut procéder de la même manière mais avec des barres horizontales.
Voici le même exemple (plot_barh_chart.py) :
Warning: file_get_contents(polytech/plot_barh_chart.py): Failed to open stream: No such file or directory in /home/jeanmichel.richer/public_html/ez_web.php on line 418
Afficher le code polytech/plot_barh_chart.py
5.4. Camembert (pie)
Le camembert ou (pie chart en anglais) permet également, tout comme les graphes de barres, de donner une idée de la répartition des données mais sous forme de pourcentage.
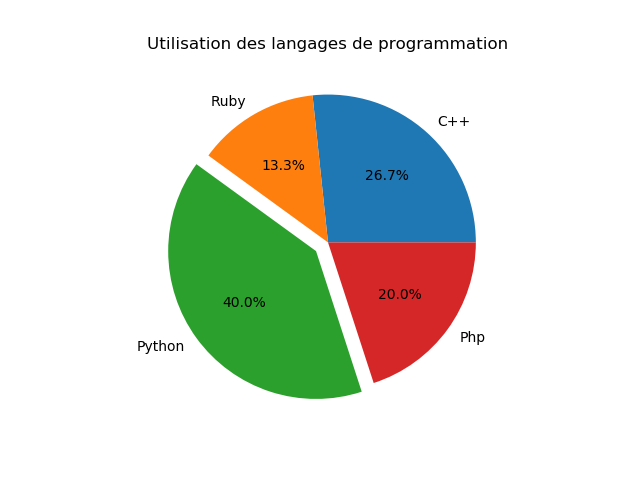
Le code du camembert est le suivant (plot_pie_chart.py) :
Warning: file_get_contents(polytech/plot_pie_chart.py): Failed to open stream: No such file or directory in /home/jeanmichel.richer/public_html/ez_web.php on line 418
Afficher le code polytech/plot_pie_chart.py
Exercice 5.3
Afficher un graphique sous forme de camembert pour un ensemble de valeurs générées
aléatoirement. Faire en sorte que la valeur la plus grande soit détachée du graphique.
5.5. Graphe de points (scatter)
5.5.1. Exemple classique
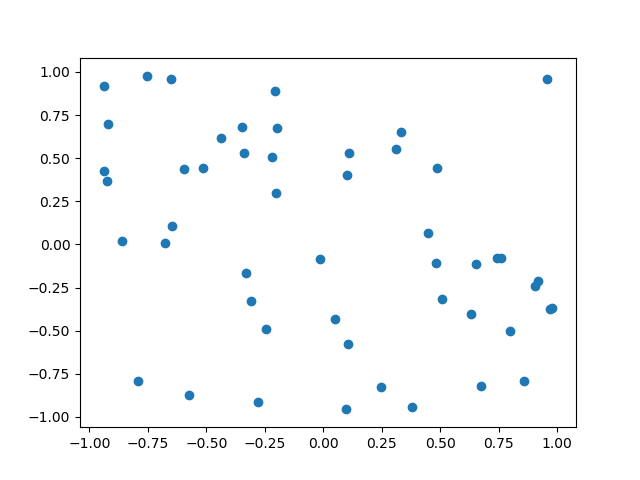
Dans certains cas, on dispose de données éparses et on désire les afficher afin de savoir si elle sont corrélées.
Voici un premier exemple généré de manière aléatoire en utilisant numpy (plot_scatter_random.py) :
Warning: file_get_contents(polytech/plot_scatter_random.py): Failed to open stream: No such file or directory in /home/jeanmichel.richer/public_html/ez_web.php on line 418
Afficher le code polytech/plot_scatter_random.py
Le deuxième exemple utilise une fonction linéaire pour associer les données (plot_scatter_correlated.py) :
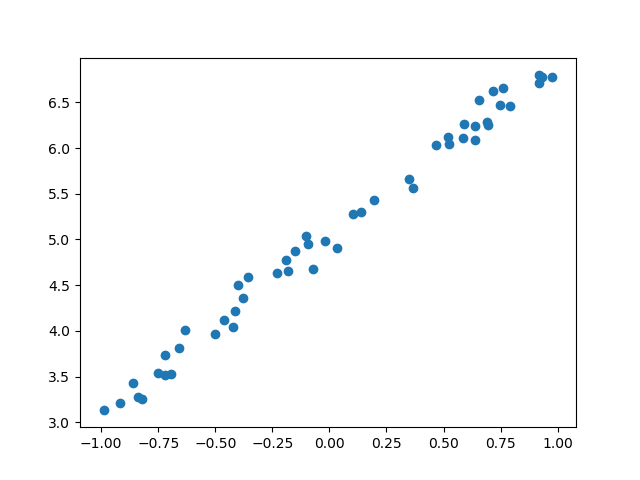
Warning: file_get_contents(polytech/plot_scatter_correlated.py): Failed to open stream: No such file or directory in /home/jeanmichel.richer/public_html/ez_web.php on line 418
Afficher le code polytech/plot_scatter_correlated.py
5.5.2. Exemple des iris
Un exemple classique utilisé en Apprentissage est celui des iris de Fisher. On dispose de données concernant trois espéces d'iris (Setosa, Versicolor, Virginica) qui concernent la longueur et largeur de leurs pétales et sépales.
"sepal.length","sepal.width","petal.length","petal.width","variety"
5.1,3.5,1.4,.2,"Setosa"
4.9,3,1.4,.2,"Setosa"
4.7,3.2,1.3,.2,"Setosa"
4.6,3.1,1.5,.2,"Setosa"
5,3.6,1.4,.2,"Setosa"
...

On désire afficher, en fonction de la longueur et largeur des sépales, la catégorie à laquelle appartient l'iris.
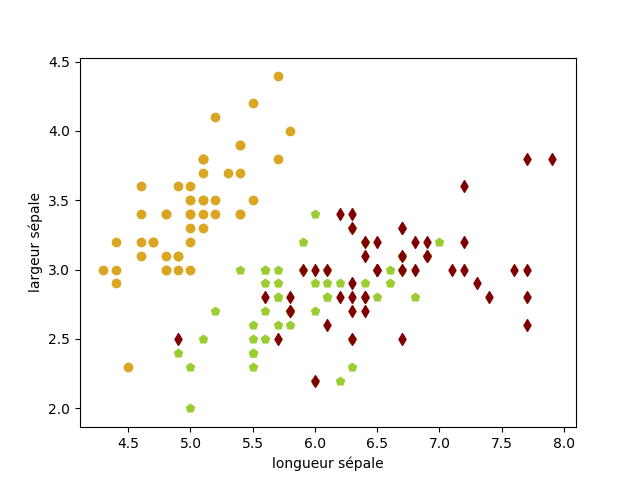
Le code associé à l'image précédente est le suivant (plot_scatter_iris_sepal.py) :
Warning: file_get_contents(polytech/plot_scatter_iris_sepal.py): Failed to open stream: No such file or directory in /home/jeanmichel.richer/public_html/ez_web.php on line 418
Afficher le code polytech/plot_scatter_iris_sepal.py
Exercice 5.4
Affichez la corrélation entre longueur et largeur des pétales. Qu'observe t-on ?
5.5.3. Exemple pairplot des iris
Un autre type de graphique intéressant pour établir des corrélations entre données est le pairplot que l'on peut générer en utilisant la bibliothèque seaborn (plot_pairplot.py) :
Warning: file_get_contents(polytech/plot_pairplot.py): Failed to open stream: No such file or directory in /home/jeanmichel.richer/public_html/ez_web.php on line 418
Afficher le code polytech/plot_pairplot.py
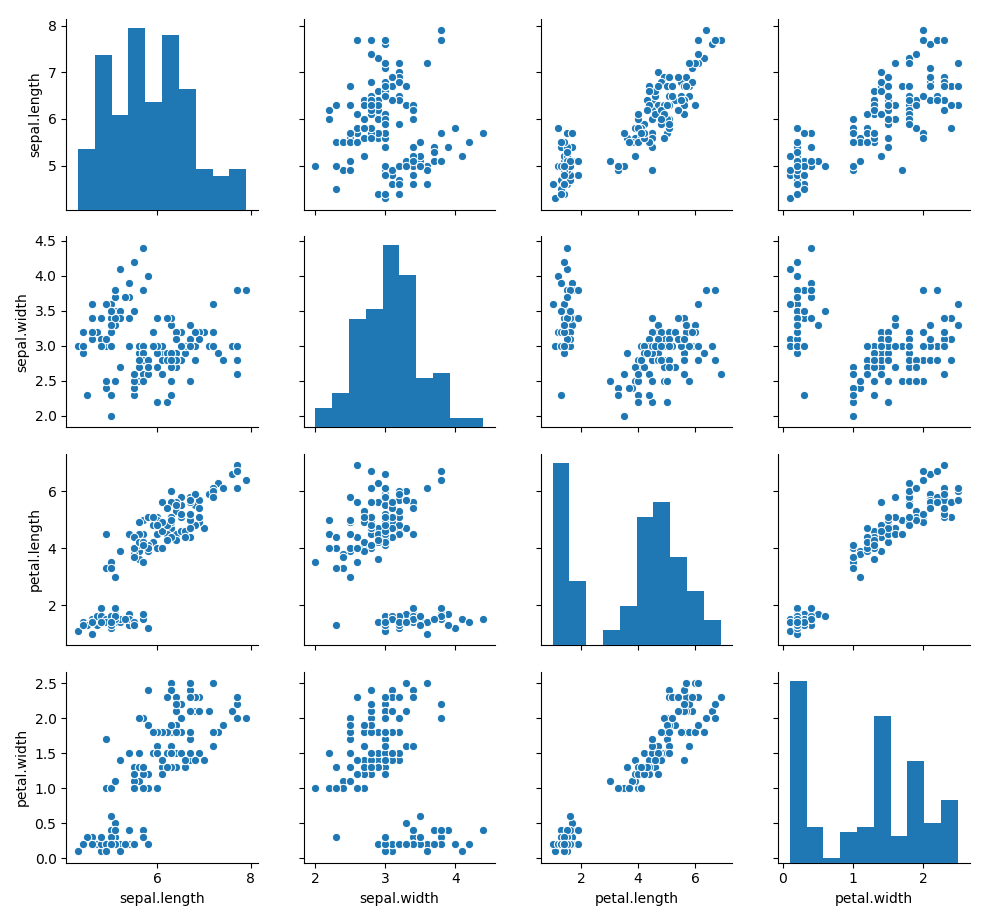
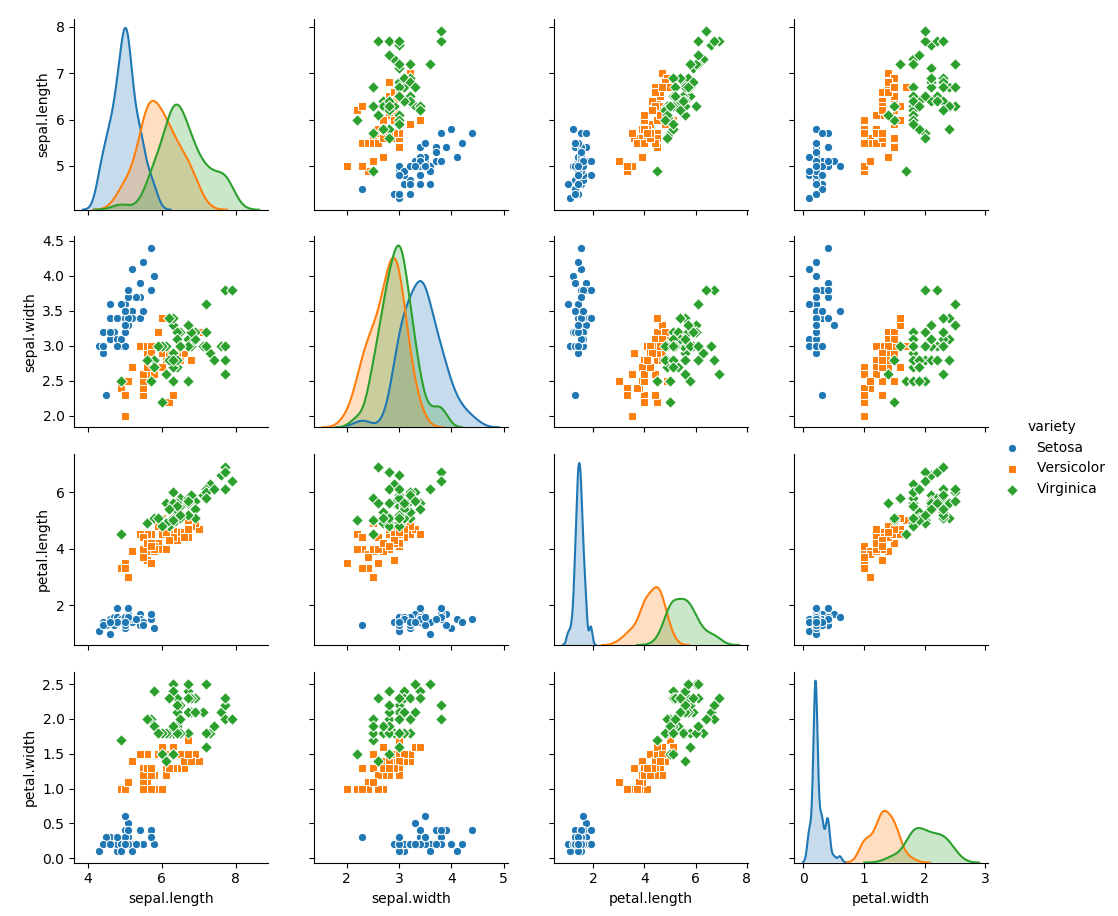
Le code précédent génère 3 graphiques :
 |
 |
 |
- le premier graphique (couleur bleu) affiche les fréquences des valeurs pour chaque variable sous forme d'un histogramme
- le second graphique affiche les données en fonction de l'espèce (variety) ce qui permet de voir que les espèces sont identifiables
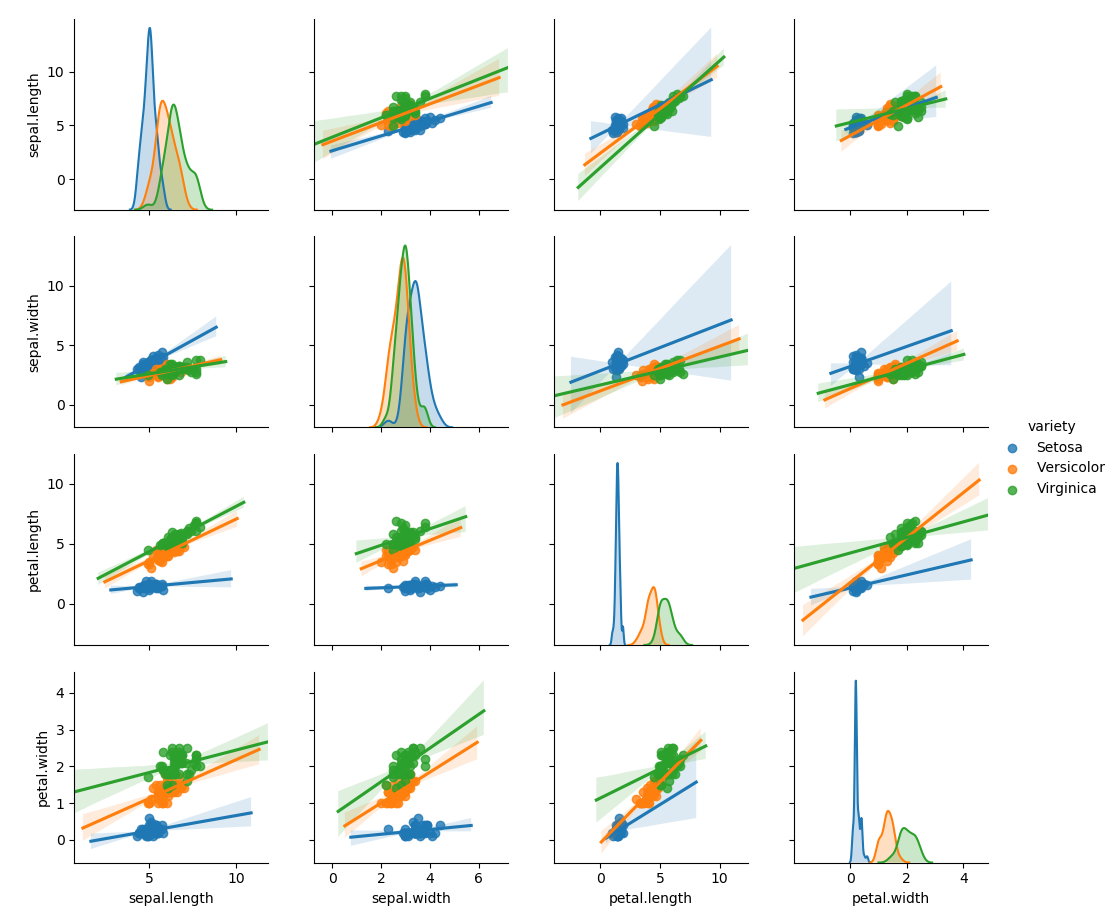
- le troisième graphique établit les régressions entre variables
On remarquera que les deuxième et troisième graphiques affichent sur la diagonale une Estimation par noyau (en anglais : Kernel Density Estimation) des données. Pour ce genre de graphe on utilise une gaussienne qui sera de coordonnée sur y d'autant plus grande que les données sont centrées autour de x.