<< Page principale

5. Le problème du voyageur de commerce

5.1. Définition

Le problème du voyageur de commerce (Travelling Salesman Problem) est définit comme suit :

Etant donné un ensemble de villes et connaissant les distances entre ces villes, trouver un plus court chemin partant d'une ville $A$ et terminant en $A$ qui passe par chaque ville une seule fois.

En fait le problème consiste à trouver le plus court cycle hamiltonien dans un graphe $G=(V,E)$ dont les sommets sont les villes et les arcs sont les distances entre les villes.

Quelle est la complexité du problème ?

Etant donné $n$ sommets d'un graphe, on a:

La complexité est donc $O(n!)$, sachant que la ville de départ n'a pas d'importance, on peut dire qu'elle est de $(n-1)!$.

Dans le cas du TSP, on ne dispose que des distances entre villes, or, une représentation en deux dimensions permettrait de résoudre le problème plus simplement (cf. exemple ci-dessous).

5.2. Exemple

Voici un exemple dont les données sont tirées de ce site.

villes = [ 
"1. New York, NY", 
"2. Los Angeles, CA", 
"3. Chicago, IL", 
"4. Minneapolis, MN", 
"5. Denver, CO", 
"6. Dallas, TX", 
"7. Seattle, WA", 
"8.Boston, MA",  
"9. San Francisco, CA", 
"10. St. Louis, MI", 
"11. Houston, TX", 
"12. Phoenix, AZ", 
"13. Salt Lake City" ]


distances = [
      [0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972],
      [2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579],
      [713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260],
      [1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987],
      [1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371],
      [1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999],
      [2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701],
      [213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099],
      [2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600],
      [875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162],
      [1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200],
      [2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504],
      [1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0]
]

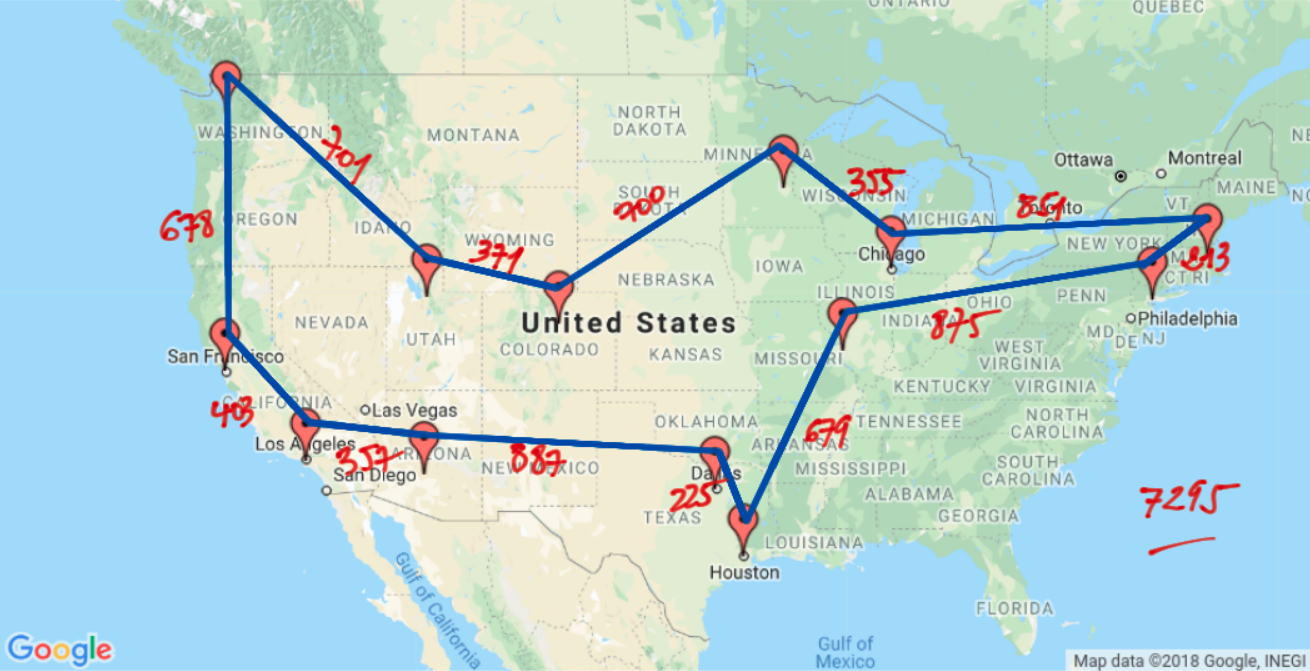
Un chemin suboptimal, que l'on ne trouvera pas avec l'algorithme glouton qu'il faut développer par la suite, devrait être celui-ci :

Le meilleur chemin (optimal), de coût 7293, étant celui-ci :

[9, 2, 12, 11, 6, 10, 1, 8, 3, 4, 5, 13, 7]

Soit le parcours suivant :

------------------------------------------
         ville            | dist. | totale
------------------------------------------
9. San Francisco, CA      |     0 |     0
2. Los Angeles, CA        |   403 |   403
12. Phoenix, AZ           |   357 |   760
11. Houston, TX           |  1017 |  1777
6. Dallas, TX             |   225 |  2002
10. St. Louis, MI         |   547 |  2549
1. New York, NY           |   875 |  3424
8. Boston, MA             |   213 |  3637
3. Chicago, IL            |   851 |  4488
4. Minneapolis, MN        |   355 |  4843
5. Denver, CO             |   700 |  5543
13. Salt Lake City, UT    |   371 |  5914
7. Seattle, WA            |   701 |  6615
9. San Francisco, CA      |   678 |  7293

5.2.1. Algorithme glouton

Exercice 5.1

Partant de la ville de New York, choisir la ville la plus proche à chaque étape et calculer le chemin et sa longueur en miles. Il s'agit d'un algorithme glouton qui fait le meilleur choix à chaque étape dans l'espoir de trouver la meilleur solution.

On doit obtenir le résultat suivant :

chemin= [1, 8, 3, 10, 4, 5, 13, 12, 2, 9, 7, 6, 11]

------------------------------------------
         ville            | dist. | totale
------------------------------------------
1. New York, NY           |     0 |     0
8. Boston, MA             |   213 |   213
3. Chicago, IL            |   851 |  1064
10. St. Louis, MI         |   262 |  1326
4. Minneapolis, MN        |   466 |  1792
5. Denver, CO             |   700 |  2492
13. Salt Lake City, UT    |   371 |  2863
12. Phoenix, AZ           |   504 |  3367
2. Los Angeles, CA        |   357 |  3724
9. San Francisco, CA      |   403 |  4127
7. Seattle, WA            |   678 |  4805
6. Dallas, TX             |  1681 |  6486
11. Houston, TX           |   225 |  6711
1. New York, NY           |  1420 |  8131

Créer une classe TSP (pour Travelling Salesman Problem) qui stocke les données des villes et des distances entre villes. Afin de simplifier le codage par la suite, on stockera les données en commençant à l'indice 1. Pour la matrice des distances cela implique d'ajouter une ligne et une colonne de 0. On peut utiliser numpy afin de stocker la matrice.

tsp_glouton.py

  1. # ###################################################################
  2. #
  3. #       Program: tsp_glouton.py
  4. #        Author: Jean-Michel Richer
  5. #  Organisation: Computer Science Department,
  6. #                University of Angers,
  7. #                France
  8. #         Email: jean-michel.richer@univ-angers.fr
  9. # Creation date: April, 2021
  10. #  Modification: April, 2021
  11. #
  12. # ###################################################################
  13. #
  14. # Aim:
  15. #
  16. #    This program is an implementation of a greedy search algorithm
  17. #    used to find a solution to the travelling salesman problem.
  18. #    At each step we choose the nearest city.
  19. #
  20. #
  21. # Objectif :
  22. #
  23. #    Ce programme repose sur l'utilisation d'un algorithme glouton
  24. #    afin de résoudre le problème du voyageur de commerce.
  25. #    A chaque étape nous choisissons la ville la plus proche de
  26. #    la ville actuelle.
  27. #
  28. # ###################################################################
  29. #
  30. # License
  31. #
  32. #    This program is a free software you can modifiy it and
  33. #    redistribute it for non profitable use.
  34. #
  35. # ###################################################################
  36.  
  37.  
  38.  
  39. """
  40. Les données de ce problème sont issues du site suivant :
  41.  
  42. https://developers.google.com/optimization/routing/tsp#c++
  43.  
  44. """
  45. import sys
  46. import numpy as np
  47.  
  48. # ===================================================================
  49. # Les données en entrée sont les suivantes :
  50. # - une liste des villes sous forme de liste de chaines de caractères
  51. # - les distances entre les villes sous forme d'une matrice d'entiers
  52. #   (en l'occurrence il s'agit d'une liste de liste d'entiers)
  53. # ===================================================================
  54.  
  55. villes = [ "1. New York, NY",
  56.     "2. Los Angeles, CA",
  57.     "3. Chicago, IL",
  58.     "4. Minneapolis, MN",
  59.     "5. Denver, CO",
  60.     "6. Dallas, TX",
  61.     "7. Seattle, WA",
  62.     "8. Boston, MA",  
  63.     "9. San Francisco, CA",
  64.     "10. St. Louis, MI",
  65.     "11. Houston, TX",
  66.     "12. Phoenix, AZ",
  67.     "13. Salt Lake City, UT" ]
  68.  
  69. distances = [
  70.       [0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972],
  71.       [2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579],
  72.       [713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260],
  73.       [1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987],
  74.       [1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371],
  75.       [1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999],
  76.       [2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701],
  77.       [213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099],
  78.       [2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600],
  79.       [875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162],
  80.       [1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200],
  81.       [2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504],
  82.       [1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0]
  83. ]
  84.  
  85.  
  86. # ===================================================================
  87. #   On définit une class TSP pour stocker et manipuler les données
  88. #   et résoudre le problème  
  89. # ===================================================================
  90. class TSP(object):
  91.     """
  92.     This is the main class used to solve the problem
  93.     """
  94.    
  95.     # -----------------------------------------------------
  96.     # Le constructeur modifie les données de manière à
  97.     # utiliser des indices qui commencent à 1 et non à 0
  98.     #
  99.     # On modifie la matrice des distances en ajoutant une
  100.     # ligne et une colonne de zéros, puis on convertit tous
  101.     # les 0 en une distance égale à la valeur maximum trouvée
  102.     # dans la matrice + 1, ce qui permettra de rechercher une
  103.     # distance minimum sans obtenir de zéro
  104.     # -----------------------------------------------------
  105.     def __init__( self, villes, distances ):
  106.         """
  107.         Constructor
  108.        
  109.         Parameters
  110.         ----------
  111.         villes : list of string
  112.           list of cities names
  113.         distances : list of list of int
  114.           matrix of distances between cities  
  115.         """
  116.         self.nbr_villes = len(villes)
  117.         self.villes = villes.copy()
  118.         self.villes.insert(0, "-------")
  119.        
  120.         self.distances = np.array( distances )
  121.        
  122.         # add column of 0
  123.         @@@...@@@
  124.         @@@...@@@
  125.        
  126.         # add line of 0
  127.         @@@...@@@
  128.         @@@...@@@
  129.        
  130.         # find maximum distance
  131.         maximum = @@@...@@@
  132.        
  133.         # replace all 0 distances by maximum + 1
  134.         @@@...@@@
  135.  
  136.         print("---- Matrice des distances modifiée ----")     
  137.         print(self.distances)  
  138.         self.verbose = True
  139.  
  140.     # -----------------------------------------------------
  141.     # Méthode de résolution gloutonne qui consiste à partir
  142.     # de la première ville (New York) et à se diriger à
  143.     # chaque étape vers la ville pour laquelle la distance
  144.     # est minimale
  145.     # On retourne le chemine sous forme d'une liste et la
  146.     # distance totale parcourue
  147.     # -----------------------------------------------------
  148.     def resolution_gloutonne(self):
  149.         """
  150.         Greedy search method: we start from the first city and
  151.         at each step we choose the nearest city
  152.         """
  153.        
  154.         print("=" * 30)
  155.         print("Recherche gloutonne")
  156.         print("=" * 30)
  157.        
  158.         # on commence par la première ville
  159.         ville_actuelle = 1
  160.         chemin = [ 1 ]
  161.        
  162.         # on crée une liste des villes non encore visitées
  163.         villes_a_visiter = [ ville for ville in range(2, self.nbr_villes+1) ]
  164.        
  165.         # distance parcourue
  166.         distance_parcourue = 0
  167.        
  168.         etape = 1
  169.        
  170.         # tant qu'on a pas visité toutes les villes
  171.         while len(villes_a_visiter) != 0:
  172.        
  173.             if self.verbose:
  174.                 print("---- etape ", etape, "----")
  175.                 print("villes_a_visiter=", villes_a_visiter)
  176.            
  177.             # trouver la ville dont la distance à la ville actuelle
  178.             # est minimale. Initialement il s'agit de la ville 0
  179.             # inexistante et de distance égale à la distance maximum
  180.             # plus un
  181.             distance_minimale = self.distances[0][0]
  182.             ville_la_plus_proche = 0
  183.                        
  184.             @@@...@@@
  185.             @@@...@@@
  186.             @@@...@@@
  187.  
  188.             # supprimer la ville la plus proche des villes à visiter
  189.             villes_a_visiter.remove( ville_la_plus_proche )
  190.            
  191.             # ajouter la ville la plus proche au chemin
  192.             chemin.append( ville_la_plus_proche )
  193.            
  194.             # mettre à jour la distance
  195.             distance_parcourue += distance_minimale
  196.            
  197.             # la ville actuelle devient la ville la plus proche
  198.             ville_actuelle = ville_la_plus_proche
  199.  
  200.             if self.verbose:
  201.                 print("ville la plus proche=", self.villes[ ville_la_plus_proche ])
  202.                 print("distance minimale   =", distance_minimale)
  203.                 print("distance totale     =", distance_parcourue)
  204.  
  205.             etape += 1
  206.            
  207.         # ne pas oublier d'ajouter la distance de la dernière ville
  208.         # à la première ville pour revenir sur la première ville
  209.         distance_parcourue += self.distances[ ville_actuelle ][ 1 ]
  210.        
  211.         if self.verbose:
  212.             print("---- etape ", etape, "----")
  213.             print("retour ville départ =", self.villes[ 1 ])
  214.             print("distance minimale   =", self.distances[ ville_actuelle ][ 1 ])
  215.             print("distance totale     =", distance_parcourue)
  216.        
  217.        
  218.         return chemin, distance_parcourue
  219.    
  220.     # -----------------------------------------------------
  221.     # Affichage du chemin et des distances parcourues
  222.     # -----------------------------------------------------
  223.     def print(self, chemin):
  224.         """
  225.         Display path and distances
  226.         """
  227.         print()
  228.         print("chemin=",chemin)
  229.         print()
  230.         print("------------------------------------------")
  231.         print("         ville            | dist. | totale")
  232.         print("------------------------------------------")
  233.         distance_totale = 0
  234.         print( "{0:25s} | {1:5d} | {2:5d}".format(self.villes[ chemin[0] ], 0, 0))
  235.         for ville in range(1, len(chemin)):
  236.             distance = self.distances[ chemin[ville-1] ][ chemin[ville] ]
  237.             distance_totale += distance
  238.             print( "{0:25s} | {1:5d} | {2:5d}".format(self.villes[ chemin[ville] ], distance, distance_totale))
  239.        
  240.         distance = self.distances[ chemin[ville] ][ chemin[0] ]
  241.         distance_totale += distance
  242.         print( "{0:25s} | {1:5d} | {2:5d}".format(self.villes[ chemin[0] ], distance, distance_totale))
  243.         print()
  244.            
  245.  
  246. # ===================================================================
  247. # Programme principal
  248. # ===================================================================
  249.  
  250. HELP_MESSAGE = """
  251. Program arguments are:
  252.  
  253. -h or --help
  254.     to get this message
  255.  
  256. -q or --quiet
  257.     to remove verbose mode and avoid to display graphics
  258.    
  259. """
  260.  
  261. # créer une instance du problème
  262. tsp = TSP( villes, distances )
  263.  
  264.  
  265. # gestion des arguments du programme
  266. if len(sys.argv) >= 1:
  267.     try:
  268.         for i in range(1, len(sys.argv)):
  269.             arg = sys.argv[i]
  270.             if arg == "-h" or arg == "--help":
  271.                 print( HELP_MESSAGE )
  272.  
  273.             elif arg == "-q" or arg == "--quiet":
  274.                 tsp.verbose = False            
  275.  
  276.             else:
  277.                 raise ValueError("Unexpected argument")
  278.                
  279.     except:
  280.         print("="*40)
  281.         print(sys.exc_info()[1])
  282.         print("="*40)
  283.         print( HELP_MESSAGE )
  284.         sys.exit(1)
  285.  
  286.  
  287. # obtenir le résultat après résolution gloutonne
  288. chemin, distance = tsp.resolution_gloutonne()
  289.  
  290. # affichage de la solution
  291. print("=" * 40)
  292. print("Solution")
  293. print("=" * 40)
  294. tsp.print(chemin)
  295.  
  296.  
  297.  

5.2.2. Recherche Locale

Exercice 5.2

Ecrire un algorithme de Recherche Locale qui permet de résoudre le problème du voyageur de commerce. On partira d'une solution générée aléatoirement.

On pourra créer une classe Path qui stocke une configuration du problème, c'est à dire un chemin et sa distance (score) associée.

Le voisinage est définit en échangeant les villes d'une configuration comme suit :

for i in range( 1, NBR_VILLES-2 ):
        for k in range( i+1, NBR_VILLES ):
            if i >= NBR_VILLES or k >= NBR_VILLES:
                continue
            
            échanger les villes i et k

On pourra afficher l'évolution de la distance en fonction du nombre d'itérations.

tsp_recherche_locale.py

  1. # ###################################################################
  2. #
  3. #       Program: tsp_recherche_locale.py
  4. #        Author: Jean-Michel Richer
  5. #  Organisation: Computer Science Department,
  6. #                University of Angers,
  7. #                France
  8. #         Email: jean-michel.richer@univ-angers.fr
  9. # Creation date: April, 2021
  10. #  Modification: April, 2021
  11. #
  12. # ###################################################################
  13. #
  14. # Aim:
  15. #
  16. #    This program is an implementation of a Local Search algorithm
  17. #    used to find a solution to the travelling salesman problem.
  18. #    
  19. #
  20. #
  21. # Objectif :
  22. #
  23. #    Ce programme repose sur l'implantation d'un algorithme de
  24. #    Recherche Locale afin de résoudre le problème du voyageur
  25. #    de commerce.
  26. #
  27. # ###################################################################
  28. #
  29. # License
  30. #
  31. #    This program is a free software you can modifiy it and
  32. #    redistribute it for non profitable use.
  33. #
  34. # ###################################################################
  35.  
  36.  
  37. """
  38. Les données de ce problème sont issues du site suivant :
  39.  
  40. https://developers.google.com/optimization/routing/tsp#c++
  41.  
  42. """
  43. import sys
  44. import random
  45. import numpy as np
  46. import matplotlib.pyplot as plt
  47.  
  48. # ===================================================================
  49. # Les données en entrée sont les suivantes :
  50. # - une liste des villes sous forme de liste de chaines de caractères
  51. # - les distances entre les villes sous forme d'une matrice d'entiers
  52. #   (en l'occurrence il s'agit d'une liste de liste d'entiers)
  53. # ===================================================================
  54.  
  55. villes = [ "1. New York, NY",
  56.     "2. Los Angeles, CA",
  57.     "3. Chicago, IL",
  58.     "4. Minneapolis, MN",
  59.     "5. Denver, CO",
  60.     "6. Dallas, TX",
  61.     "7. Seattle, WA",
  62.     "8. Boston, MA",  
  63.     "9. San Francisco, CA",
  64.     "10. St. Louis, MI",
  65.     "11. Houston, TX",
  66.     "12. Phoenix, AZ",
  67.     "13. Salt Lake City, UT" ]
  68.  
  69. distances = [
  70.       [0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972],
  71.       [2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579],
  72.       [713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260],
  73.       [1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987],
  74.       [1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371],
  75.       [1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999],
  76.       [2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701],
  77.       [213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099],
  78.       [2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600],
  79.       [875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162],
  80.       [1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200],
  81.       [2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504],
  82.       [1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0]
  83. ]
  84.  
  85. # ===================================================================
  86. #   On définit un chemin (configuration) comme la liste des villes
  87. #   parcourues et le coût qui lui  est associé
  88. # ===================================================================
  89. class Path(object):
  90.     """
  91.     a Path is the list of cities visited and the distance travelled
  92.     """
  93.     def __init__(self, chemin, distance):
  94.         """
  95.         Constructor
  96.        
  97.         Parameters
  98.         ----------
  99.         chemin: list of int
  100.           list of cities visited identified by their number
  101.         distance: int
  102.           distance travelled (given by the 'f_objectif'
  103.           function of class TSP)
  104.         """
  105.         self.chemin = chemin
  106.         self.distance = distance
  107.  
  108.  
  109.     def __str__(self):
  110.         return str(self.chemin) + ", " + str(self.distance)
  111.  
  112.    
  113.     def copy(self):
  114.         return type(self)(self.chemin.copy(), self.distance)
  115.        
  116. # ===================================================================
  117. #   On définit une class TSP pour stocker et manipuler les données
  118. #   et résoudre le problème
  119. #  
  120. # ===================================================================
  121. class TSP(object):
  122.     """
  123.     Class used to solve the problem that implements a Local Search
  124.     algorithm
  125.     """
  126.    
  127.     # -----------------------------------------------------
  128.     # Le constructeur modifie les données de manière à
  129.     # utiliser des indices qui commencent à 1 et non à 0
  130.     #
  131.     # On modifie la matrice des distances en ajoutant une
  132.     # ligne et une colonne de zéros, puis on convertit tous
  133.     # les 0 en une distance égale à la valeur maximum trouvée
  134.     # dans la matrice + 1, ce qui permettra de rechercher une
  135.     # distance minimum sans obtenir de zéro
  136.     # -----------------------------------------------------
  137.     def __init__( self, villes, distances ):
  138.         """
  139.         Constructor
  140.        
  141.         Parameters
  142.         ----------
  143.         villes : list of string
  144.           list of cities names
  145.         distances : list of list of int
  146.           matrix of distances between cities  
  147.         """
  148.         self.nbr_villes = len(villes)
  149.         self.villes = villes.copy()
  150.         self.villes.insert(0, "-------")
  151.        
  152.         self.distances = np.array( distances )
  153.        
  154.         # add column of 0
  155.         @@@...@@@
  156.         @@@...@@@
  157.        
  158.         # add line of 0
  159.         @@@...@@@
  160.         @@@...@@@
  161.        
  162.         # find maximum distance
  163.         maximum = @@@...@@@
  164.        
  165.         # replace all 0 distances by maximum + 1
  166.         @@@...@@@
  167.  
  168.         print("---- Matrice des distances modifiée ----")     
  169.         print(self.distances)  
  170.        
  171.         self.verbose = True
  172.         self.graphics = False
  173.  
  174.    
  175.     # -----------------------------------------------------
  176.     # Définition de la fonction objectif
  177.     # -----------------------------------------------------
  178.     def f_objectif( self, chemin ):
  179.         """
  180.         Compute the total distance of a path
  181.         """
  182.        
  183.         distance_parcourue = 0
  184.         @@@...@@@
  185.         @@@...@@@
  186.         @@@...@@@
  187.         return distance_parcourue  
  188.    
  189.    
  190.     # -----------------------------------------------------
  191.     # Trouve les voisins améliorants à partir d'une
  192.     # configuration
  193.     # -----------------------------------------------------
  194.     def voisinage( self, configuration ):
  195.         """
  196.         Neighborhood function that generates paths in the
  197.         neighborhood of the current path
  198.        
  199.         Parameters
  200.         ----------
  201.         configuration : path
  202.            current path
  203.         """
  204.        
  205.         # liste des voisins améliorants
  206.         l = [ ]
  207.        
  208.         distance_a_ameliorer = configuration.distance
  209.        
  210.         for i in range( 1, self.nbr_villes-2):
  211.             for k in range( i+1, self.nbr_villes):
  212.                 if i > self.nbr_villes or k > self.nbr_villes:
  213.                     continue
  214.                
  215.                @@@...@@@
  216.                
  217.                 if nouvelle_configuration.distance < distance_a_ameliorer:
  218.                     l.append( nouvelle_configuration )
  219.                
  220.         # trier les configuration par ordre croissant de la distance        
  221.         @@@...@@@
  222.      
  223.         return l
  224.    
  225.     # -----------------------------------------------------
  226.     # Méthode de résolution basée sur la recherche locale
  227.     # -----------------------------------------------------
  228.     def resolution_recherche_locale(self):
  229.         """
  230.         Local search
  231.         """
  232.        
  233.         # enregistre l'évolution de la distance au cours du temps
  234.         # en fonction du nombre d'itérations
  235.         self.liste_evolution_courante = []
  236.        
  237.         #
  238.         # Génération de la configuration initiale
  239.         #
  240.        
  241.         villes_dans_le_desordre = [ x for x in range(1, self.nbr_villes+1 ) ]
  242.         random.shuffle( villes_dans_le_desordre )
  243.         configuration_courante = Path( villes_dans_le_desordre, self. f_objectif( villes_dans_le_desordre ) )
  244.  
  245.         # création de la configuration courante
  246.         self.liste_evolution_courante.append( configuration_courante.distance )
  247.        
  248.         print("Configuration initiale=", configuration_courante)
  249.        
  250.         iteration = 1
  251.        
  252.         while True:
  253.            
  254.             liste_voisins_ameliorants = self.voisinage( configuration_courante )
  255.            
  256.             # pas de voisin améliorant, on arrête la recherche
  257.             if len(liste_voisins_ameliorants) == 0:
  258.                 break
  259.            
  260.             # choix du meilleur voisin améliorant
  261.             configuration_courante = liste_voisins_ameliorants[ 0 ]
  262.            
  263.             if self.verbose:
  264.                 print("=> ", iteration, ": voisins améliorants=", len(liste_voisins_ameliorants), "configuration=",configuration_courante)
  265.                
  266.             iteration += 1
  267.            
  268.             self.liste_evolution_courante.append( configuration_courante.distance )
  269.                
  270.         return configuration_courante
  271.    
  272.     # -----------------------------------------------------
  273.     # Affichage du chemin ainsi que des distances
  274.     # parcourues et de la distance totale
  275.     # -----------------------------------------------------        
  276.     def print(self, chemin):
  277.         print()
  278.         print("chemin=",chemin)
  279.         print()
  280.         print("------------------------------------------")
  281.         print("         ville            | dist. | totale")
  282.         print("------------------------------------------")
  283.         distance_totale = 0
  284.         print( "{0:25s} | {1:5d} | {2:5d}".format(self.villes[ chemin[0] ], 0, 0))
  285.         for ville in range(1, len(chemin)):
  286.             distance = self.distances[ chemin[ville-1] ][ chemin[ville] ]
  287.             distance_totale += distance
  288.             print( "{0:25s} | {1:5d} | {2:5d}".format(self.villes[ chemin[ville] ], distance, distance_totale))
  289.        
  290.         distance = self.distances[ chemin[ville] ][ chemin[0] ]
  291.         distance_totale += distance
  292.         print( "{0:25s} | {1:5d} | {2:5d}".format(self.villes[ chemin[0] ], distance, distance_totale))
  293.         print()
  294.  
  295.     # -----------------------------------------------------
  296.     # Affiche un graphique de l'évolution du score
  297.     # (distance) de la configuration courante
  298.     # -----------------------------------------------------
  299.     def graphique(self):
  300.         if not self.verbose:
  301.             return
  302.            
  303.         x = range( len( self.liste_evolution_courante ) )
  304.         plt.plot( x, self.liste_evolution_courante, label='configuration courante' )
  305.         plt.xlabel('itérations')
  306.         plt.title('Evolution de la recherche locale')
  307.         plt.legend()
  308.         plt.show()
  309.  
  310.            
  311. # ===================================================================
  312. # Programme principal
  313. # ===================================================================
  314.  
  315. HELP_MESSAGE = """
  316. Program arguments are:
  317.  
  318. -h or --help
  319.     to get this message
  320.  
  321. -q or --quiet
  322.     to remove verbose mode and avoid to display graphics
  323.    
  324. """
  325.  
  326. # creer une instance du problème
  327. tsp = TSP( villes, distances )
  328.  
  329. # gestion des arguments du programme
  330. if len(sys.argv) >= 1:
  331.     try:
  332.         for i in range(1, len(sys.argv)):
  333.             arg = sys.argv[i]
  334.             if arg == "-h" or arg == "--help":
  335.                 print( HELP_MESSAGE )
  336.  
  337.             elif arg == "-q" or arg == "--quiet":
  338.                 tsp.verbose = False            
  339.  
  340.             else:
  341.                 raise ValueError("Unexpected argument")
  342.                
  343.     except:
  344.         print("="*40)
  345.         print(sys.exc_info()[1])
  346.         print("="*40)
  347.         print( HELP_MESSAGE )
  348.         sys.exit(1)
  349.        
  350. # start local search
  351. configuration_finale = tsp.resolution_recherche_locale()
  352.  
  353. tsp.print(configuration_finale.chemin)
  354. tsp.graphique()
  355.  
  356. #
  357. # Trace de l'obtention de l'optimum
  358. #
  359. #Configuration initiale= [4, 12, 10, 9, 8, 3, 11, 13, 2, 1, 5, 6, 7], 18386
  360. #=>  1 : voisins améliorants= 43 configuration= [4, 12, 10, 1, 8, 3, 11, 13, 2, 9, 5, 6, 7], 12301
  361. #=>  2 : voisins améliorants= 19 configuration= [4, 6, 10, 1, 8, 3, 11, 13, 2, 9, 5, 12, 7], 10514
  362. #=>  3 : voisins améliorants= 14 configuration= [4, 6, 10, 1, 8, 3, 11, 12, 2, 9, 5, 13, 7], 9481
  363. #=>  4 : voisins améliorants= 5 configuration= [4, 6, 10, 1, 8, 3, 11, 12, 2, 9, 7, 13, 5], 8515
  364. #=>  5 : voisins améliorants= 3 configuration= [4, 3, 10, 1, 8, 6, 11, 12, 2, 9, 7, 13, 5], 7708
  365. #=>  6 : voisins améliorants= 4 configuration= [4, 3, 8, 1, 10, 6, 11, 12, 2, 9, 7, 13, 5], 7293
  366.  
  367.  

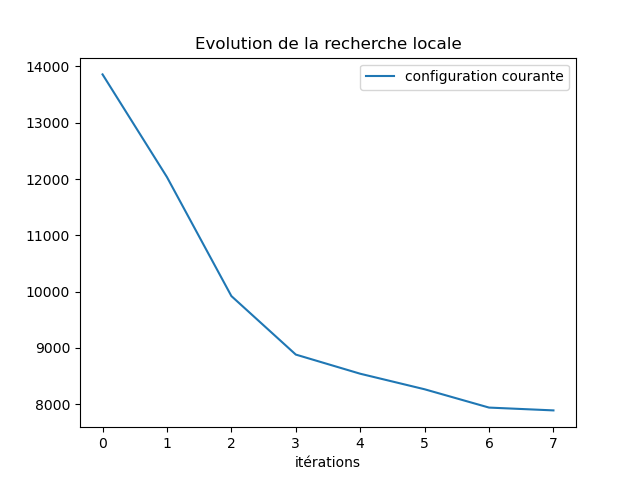
On pourra enregistrer le score (distance) de la configuration au cours des itérations et dessiner le graphique qui en résulte comme par exemple :

5.2.3. Recuit Simulé

Exercice 5.3

Ecrire un algorithme de Recuit Simulé qui permet de résoudre le problème du voyageur de commerce. On partira d'une solution générée aléatoirement et on utilisera le même voisinage que précédemment.

Les paramètres de l'algorithme sont les suivants :

  • la température initiale $T_0 = 100.0$
  • la température finale $T_f = 0.0001$
  • le facteur de refroidissement $α = 0.999$

tsp_recuit_simule.py

  1. # ###################################################################
  2. #
  3. #       Program: tsp_recuit_simule.py
  4. #        Author: Jean-Michel Richer
  5. #  Organisation: Computer Science Department,
  6. #                University of Angers,
  7. #                France
  8. #         Email: jean-michel.richer@univ-angers.fr
  9. # Creation date: April, 2021
  10. #  Modification: April, 2021
  11. #
  12. # ###################################################################
  13. #
  14. # Aim:
  15. #
  16. #    This program is an implementation of a Simulated Annealing
  17. #    algorithm used to find a solution to the travelling salesman
  18. #    problem.
  19. #
  20. # Objectif :
  21. #
  22. #    Ce programme repose sur l'implantation d'un algorithme de
  23. #    Recuit Simulé afin de résoudre le problème du voyageur
  24. #    de commerce.
  25. #
  26. # ###################################################################
  27. #
  28. # License
  29. #
  30. #    This program is a free software you can modifiy it and
  31. #    redistribute it for non profitable use.
  32. #
  33. # ###################################################################
  34.  
  35. #
  36. # Sous cette forme l'algorithme peut parfois atteindre la solution
  37. #
  38. #[2, 3, 8, 0, 6, 5, 11, 7, 4, 9, 12, 1, 10], 18406
  39. #=>  1 :  [2, 3, 7, 0, 6, 5, 11, 8, 4, 9, 12, 1, 10], 13120
  40. #=>  2 :  [2, 3, 7, 0, 9, 5, 11, 8, 4, 6, 12, 1, 10], 10217
  41. #=>  3 :  [2, 3, 7, 0, 9, 5, 11, 8, 1, 6, 12, 4, 10], 8906
  42. #=>  4 :  [2, 3, 7, 0, 9, 5, 11, 1, 8, 6, 12, 4, 10], 8329
  43. #=>  5 :  [2, 3, 7, 0, 10, 5, 11, 1, 8, 6, 12, 4, 9], 7791
  44. #=>  6 :  [2, 9, 7, 0, 10, 5, 11, 1, 8, 6, 12, 4, 3], 7610
  45. #=>  7 :  [2, 0, 7, 9, 10, 5, 11, 1, 8, 6, 12, 4, 3], 7320
  46. #=>  8 :  [2, 7, 0, 9, 10, 5, 11, 1, 8, 6, 12, 4, 3], 7295
  47. #=>  9 :  [2, 7, 0, 9, 5, 10, 11, 1, 8, 6, 12, 4, 3], 7293
  48.  
  49. #[8, 6, 10, 7, 4, 1, 2, 9, 12, 3, 5, 11, 0], 17395
  50. #=>  1 :  [8, 6, 10, 7, 4, 0, 2, 9, 12, 3, 5, 11, 1], 13207
  51. #=>  2 :  [8, 6, 10, 4, 7, 0, 2, 9, 12, 3, 5, 11, 1], 11063
  52. #=>  3 :  [8, 6, 12, 4, 7, 0, 2, 9, 10, 3, 5, 11, 1], 8951
  53. #=>  4 :  [8, 6, 12, 4, 7, 0, 2, 9, 3, 10, 5, 11, 1], 8101
  54. #=>  5 :  [8, 6, 12, 4, 7, 0, 2, 3, 9, 10, 5, 11, 1], 7817
  55. #=>  6 :  [8, 6, 12, 4, 2, 0, 7, 3, 9, 10, 5, 11, 1], 7736
  56. #=>  7 :  [8, 6, 12, 4, 3, 0, 7, 2, 9, 10, 5, 11, 1], 7345
  57. #=>  8 :  [8, 6, 12, 4, 3, 2, 7, 0, 9, 10, 5, 11, 1], 7295
  58. #=>  9 :  [8, 6, 12, 4, 3, 2, 7, 0, 9, 5, 10, 11, 1], 7293
  59.  
  60. import random
  61. import sys
  62. import math
  63. import numpy as np
  64. import matplotlib.pyplot as plt
  65.  
  66.  
  67. # ===================================================================
  68. # Les données en entrée sont les suivantes :
  69. # - une liste des villes sous forme de liste de chaines de caractères
  70. # - les distances entre les villes sous forme d'une matrice d'entiers
  71. #   (en l'occurrence il s'agit d'une liste de liste d'entiers)
  72. # ===================================================================
  73.  
  74. villes = [ "1. New York, NY",
  75.     "2. Los Angeles, CA",
  76.     "3. Chicago, IL",
  77.     "4. Minneapolis, MN",
  78.     "5. Denver, CO",
  79.     "6. Dallas, TX",
  80.     "7. Seattle, WA",
  81.     "8. Boston, MA",  
  82.     "9. San Francisco, CA",
  83.     "10. St. Louis, MI",
  84.     "11. Houston, TX",
  85.     "12. Phoenix, AZ",
  86.     "13. Salt Lake City, UT" ]
  87.  
  88.  
  89. distances = [
  90.       [0, 2451, 713, 1018, 1631, 1374, 2408, 213, 2571, 875, 1420, 2145, 1972],
  91.       [2451, 0, 1745, 1524, 831, 1240, 959, 2596, 403, 1589, 1374, 357, 579],
  92.       [713, 1745, 0, 355, 920, 803, 1737, 851, 1858, 262, 940, 1453, 1260],
  93.       [1018, 1524, 355, 0, 700, 862, 1395, 1123, 1584, 466, 1056, 1280, 987],
  94.       [1631, 831, 920, 700, 0, 663, 1021, 1769, 949, 796, 879, 586, 371],
  95.       [1374, 1240, 803, 862, 663, 0, 1681, 1551, 1765, 547, 225, 887, 999],
  96.       [2408, 959, 1737, 1395, 1021, 1681, 0, 2493, 678, 1724, 1891, 1114, 701],
  97.       [213, 2596, 851, 1123, 1769, 1551, 2493, 0, 2699, 1038, 1605, 2300, 2099],
  98.       [2571, 403, 1858, 1584, 949, 1765, 678, 2699, 0, 1744, 1645, 653, 600],
  99.       [875, 1589, 262, 466, 796, 547, 1724, 1038, 1744, 0, 679, 1272, 1162],
  100.       [1420, 1374, 940, 1056, 879, 225, 1891, 1605, 1645, 679, 0, 1017, 1200],
  101.       [2145, 357, 1453, 1280, 586, 887, 1114, 2300, 653, 1272, 1017, 0, 504],
  102.       [1972, 579, 1260, 987, 371, 999, 701, 2099, 600, 1162, 1200, 504, 0]
  103. ]
  104.  
  105.  
  106. # ===================================================================
  107. #   On définit un chemin (configuration) comme la liste des villes
  108. #   parcourues et le coût qui lui  est associé
  109. # ===================================================================
  110. class Path(object):
  111.     """
  112.    a Path is the list of cities visited and the distance travelled
  113.    """
  114.     def __init__(self, chemin, distance):
  115.         self.chemin = chemin
  116.         self.distance = distance
  117.  
  118.     def __str__(self):
  119.         return str(self.chemin) + ", " + str(self.distance)
  120.    
  121.     def copy(self):
  122.         return type(self)(self.chemin.copy(), self.distance)
  123.        
  124. # ===================================================================
  125. #   On définit une class TSP pour stocker et manipuler les données
  126. #   et résoudre le problème
  127. #  
  128. # ===================================================================
  129. class TSP(object):
  130.     """
  131.     Class used to solve the problem that implements a Local Search
  132.     algorithm
  133.     """
  134.    
  135.     # -----------------------------------------------------
  136.     # Le constructeur modifie les données de manière à
  137.     # utiliser des indices qui commencent à 1 et non à 0
  138.     #
  139.     # On modifie la matrice des distances en ajoutant une
  140.     # ligne et une colonne de zéros, puis on convertit tous
  141.     # les 0 en une distance égale à la valeur maximum trouvée
  142.     # dans la matrice + 1, ce qui permettra de rechercher une
  143.     # distance minimum sans obtenir de zéro
  144.     # -----------------------------------------------------
  145.     def __init__( self, villes, distances ):
  146.         """
  147.         Constructor
  148.        
  149.         Parameters
  150.         ----------
  151.         villes : list of string
  152.           list of cities names
  153.         distances : list of list of int
  154.           matrix of distances between cities  
  155.         """
  156.         self.nbr_villes = len(villes)
  157.         self.villes = villes.copy()
  158.         self.villes.insert(0, "-------")
  159.        
  160.         self.distances = np.array( distances )
  161.        
  162.         # add column of 0
  163.         @@@...@@@
  164.         @@@...@@@
  165.        
  166.         # add line of 0
  167.         @@@...@@@
  168.         @@@...@@@
  169.        
  170.         # find maximum distance
  171.         maximum = @@@...@@@
  172.        
  173.         # replace all 0 distances by maximum + 1
  174.         @@@...@@@
  175.  
  176.         print("---- Matrice des distances modifiée ----")     
  177.         print(self.distances)
  178.    
  179.         self.verbose = True
  180.  
  181.     # -----------------------------------------------------
  182.     # Définition de la fonction objectif
  183.     # -----------------------------------------------------
  184.     def f_objectif( self, chemin ):
  185.         distance_parcourue = 0
  186.        
  187.         @@@...@@@
  188.        
  189.         return distance_parcourue  
  190.    
  191.     # -----------------------------------------------------
  192.     # Génération de voisins en échangeant des villes deux
  193.     # à deux. Seules les configurations voisines amélio-
  194.     # rantes sont gardées puis triées en ordre croissant.
  195.     # En fonction du nombre d'itérations on élimine
  196.     # certaines configurations :
  197.     # - si le nombre d'itérations est inférieu à 1000, on
  198.     #   ne garde que les dix premières configurations
  199.     #   améliorantes
  200.     # - au dela de 5000 itérations on ne garde que la
  201.     #   première configuration améliorante
  202.     # -----------------------------------------------------
  203.     def voisinage( self, configuration, iteration ):
  204.  
  205.         # liste des voisins améliorants
  206.         l = [ ]
  207.        
  208.         distance_a_ameliorer = int(configuration.distance * 1.1)
  209.        
  210.         for i in range( 1, self.nbr_villes-2):
  211.             for k in range( i+1, self.nbr_villes):
  212.                 if i > self.nbr_villes or k > self.nbr_villes:
  213.                     continue
  214.                
  215.                 @@@...@@@
  216.                
  217.                 if nouvelle_configuration.distance < distance_a_ameliorer:
  218.                     l.append( nouvelle_configuration )
  219.                
  220.         # tri des configuration en ordre croissant de la
  221.         # distance parcourue        
  222.         @@@...@@@
  223.                
  224.         return l
  225.    
  226.     # -----------------------------------------------------
  227.     # Méthode de résolution basée sur le recuit simulé
  228.     # -----------------------------------------------------
  229.     def resolution_recuit_simule(self, t_i = 100.0, t_f = 0.001, alpha = 0.99):
  230.    
  231.         self.liste_evolution_courante = []
  232.         self.liste_evolution_meilleur = []
  233.        
  234.         #
  235.         # Génération de la configuration initiale
  236.         #
  237.         villes_dans_le_desordre = [ x for x in range(1, self.nbr_villes+1) ]
  238.         random.shuffle( villes_dans_le_desordre )
  239.         configuration_courante = Path( villes_dans_le_desordre, self. f_objectif( villes_dans_le_desordre ) )
  240.  
  241.         print("Configuration initiale=", configuration_courante)
  242.        
  243.         iteration = 1
  244.        
  245.         #
  246.         # Paramètres de l'algorithme
  247.         #
  248.        
  249.         # température initiale
  250.         T_initiale = t_i
  251.         # température finale
  252.         T_finale   = t_f
  253.         # facteur de refroidissement (alpha)
  254.         facteur_de_refroidissement = alpha
  255.        
  256.         T = T_initiale
  257.         meilleure_configuration = configuration_courante.copy()
  258.  
  259.         # Tant qu'on a pas atteint la température finale
  260.         while T > T_finale:
  261.            
  262.             str_T = "{:.4f}".format(T)
  263.             str_it = str(iteration)
  264.             str_cc = str( configuration_courante.distance )
  265.             str_mc = str( meilleure_configuration.distance)
  266.             print("T=" + str_T + ",iter=" + str_it + " => " + str_cc + " ! " + str_mc, end='')
  267.            
  268.             # rechercher des voisins améliorants
  269.             l_voisins_ameliorants = self.voisinage( configuration_courante, iteration )
  270.            
  271.             # si il n'y a qu'un seul voisin améliorant on le choisit
  272.             # sinon on choisit au hasard
  273.             if len(l_voisins_ameliorants) == 1:
  274.                 i = 0
  275.             else:
  276.                 i = random.randint(0, len(l_voisins_ameliorants)-1 )
  277.                
  278.             configuration_voisine = l_voisins_ameliorants[ i ]
  279.            
  280.             str_cv = str(configuration_voisine.distance)
  281.             str_lp = str(l_voisins_ameliorants[ 0 ].distance)
  282.             str_ld = str(l_voisins_ameliorants[ len(l_voisins_ameliorants)-1 ].distance)
  283.             print(",voisin=" + str_cv + " (" + str_lp + ", " + str_ld + ")", end='')    
  284.            
  285.             delta_f = configuration_voisine.distance - configuration_courante.distance
  286.  
  287.             str_u = ""
  288.             str_exp = ""
  289.            
  290.             # si le voisin est meilleur que la configuration courante
  291.             #    on le garde
  292.             # sinon
  293.             #    on prend un voisin qui détériore la solution
  294.             #    avec une certaine probabilité qui diminue à
  295.             #    mesure que la température diminue
  296.             if delta_f < 0.0:
  297.                 configuration_courante = configuration_voisine
  298.             else:
  299.                 # générer une valeur entre 0 et 1.0
  300.                 u = @@@...@@@
  301.                 # calculer exp(-delta_f / T)
  302.                 e = @@@...@@@
  303.                    
  304.                 str_u = "{:.4f}".format(u)
  305.                 str_exp = "{:.4f}".format(e)
  306.                
  307.                 if (e > u):
  308.                     configuration_courante = configuration_voisine
  309.                    
  310.             str_delta_f = "{:.4f}".format(delta_f)
  311.             print(",delta_f="+str_delta_f+",u="+str_u+",exp="+str_exp)
  312.                
  313.             if  configuration_courante.distance < meilleure_configuration.distance:
  314.                 meilleure_configuration = configuration_courante.copy()
  315.            
  316.             # diminution de la température   
  317.             T = facteur_de_refroidissement * T    
  318.             iteration += 1
  319.  
  320.             self.liste_evolution_courante.append( configuration_courante.distance )
  321.             self.liste_evolution_meilleur.append( meilleure_configuration.distance )
  322.            
  323.         return meilleure_configuration
  324.                
  325.     # -----------------------------------------------------
  326.     # Affichage du chemin ainsi que des distances
  327.     # parcourues et de la distance totale
  328.     # -----------------------------------------------------
  329.     def print(self, chemin):
  330.         print()
  331.         print("chemin=",chemin)
  332.         print()
  333.         print("------------------------------------------")
  334.         print("         ville            | dist. | totale")
  335.         print("------------------------------------------")
  336.         distance_totale = 0
  337.         print( "{0:25s} | {1:5d} | {2:5d}".format(self.villes[ chemin[0] ], 0, 0))
  338.         for ville in range(1, len(chemin)):
  339.             distance = self.distances[ chemin[ville-1] ][ chemin[ville] ]
  340.             distance_totale += distance
  341.             print( "{0:25s} | {1:5d} | {2:5d}".format(self.villes[ chemin[ville] ], distance, distance_totale))
  342.        
  343.         distance = self.distances[ chemin[ville] ][ chemin[0] ]
  344.         distance_totale += distance
  345.         print( "{0:25s} | {1:5d} | {2:5d}".format(self.villes[ chemin[0] ], distance, distance_totale))
  346.         print()
  347.    
  348.     # -----------------------------------------------------
  349.     # Affiche un graphique de l'évolution des scores
  350.     # (distances) de la configuration courante et de la
  351.     # meilleure configuration
  352.     # -----------------------------------------------------
  353.     def graphique(self):
  354.         x = range( len( self.liste_evolution_courante ) )
  355.         plt.grid()
  356.         plt.plot( x, self.liste_evolution_courante, label='configuration courante' )
  357.         plt.plot( x, self.liste_evolution_meilleur, label='meilleure configuration' )
  358.         plt.xlabel('itérations')
  359.         plt.legend()
  360.         plt.title('Evolution du Recuit Simulé')
  361.         plt.show()
  362.            
  363. # ===================================================================
  364. # Programme principal
  365. # ===================================================================
  366.  
  367. HELP_MESSAGE = """
  368. Program arguments are:
  369.  
  370. -h or --help
  371.     to get this message
  372.  
  373. -q or --quiet
  374.     to remove verbose mode and avoid to display graphics
  375.    
  376. -i float or --t_init=float
  377.     initial temperature (default is 100.0)
  378.    
  379. -f float or --t_final=float
  380.     final temperature (default is 0.001)
  381.    
  382. -a float or --alpha=float      
  383.     cooling factor (default is 0.99)
  384. """
  385.  
  386. # creer une instance du problème
  387. tsp = TSP( villes, distances )
  388.  
  389. # température initiale
  390. t_i = 100.0
  391. # température finale
  392. t_f = 0.001
  393. #facteur_de_refroidissement
  394. alpha = 0.99
  395.  
  396. #
  397. # gestion des arguments du programme
  398. #
  399. if len(sys.argv) >= 1:
  400.     try:
  401.    
  402.         i = 1
  403.         while i < len(sys.argv):
  404.             arg = sys.argv[i]
  405.             print(i, arg)
  406.             if arg == "-h" or arg == "--help":
  407.                 print( HELP_MESSAGE )
  408.                
  409.             elif arg == "-q" or arg == "--quiet":
  410.                 tsp.verbose = False
  411.                
  412.             elif arg == "-i":
  413.                 i += 1
  414.                 t_i = float(sys.argv[i])
  415.             elif arg.startswith("--t_init="):
  416.                 t_i = float(arg.split('=')[1])
  417.                
  418.             elif arg == "-f":
  419.                 i += 1
  420.                 t_f = float(sys.argv[i])
  421.             elif arg.startswith("--t_final="):
  422.                 t_f = float(arg.split('=')[1])
  423.                
  424.             elif arg == "-a":
  425.                 i += 1
  426.                 alpha = float(sys.argv[i])
  427.             elif arg.startswith("--alpha="):
  428.                 alpha = float(arg.split('=')[1])
  429.                
  430.             else:
  431.                 raise ValueError("Unexpected argument")
  432.                
  433.             i += 1
  434.        
  435.     except:
  436.         print("="*40)
  437.         print(sys.exc_info()[1])
  438.         print("="*40)
  439.         print( HELP_MESSAGE )
  440.         sys.exit(1)
  441.  
  442. #
  443. # recherche de la meilleure solution
  444. #
  445.  
  446. configuration_finale = tsp.resolution_recuit_simule(t_i, t_f, alpha)
  447.  
  448. tsp.print(configuration_finale.chemin)
  449. tsp.graphique()
  450.  
  451.  

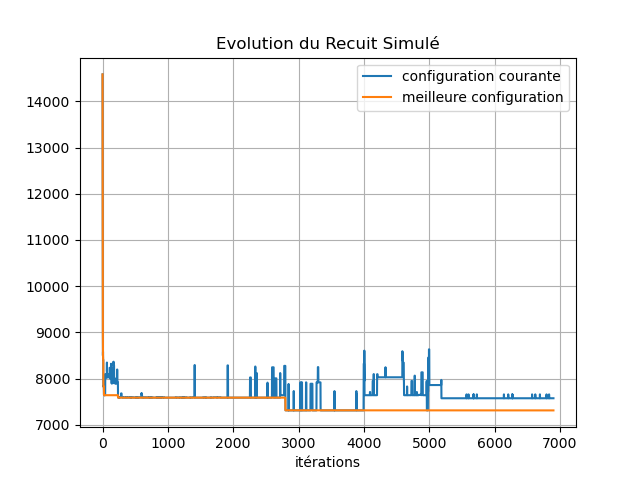
On pourra enregistrer le score (distance) de la configuration courante et de la meilleure configuration au cours des itérations et dessiner le graphique qui en résulte comme par exemple :

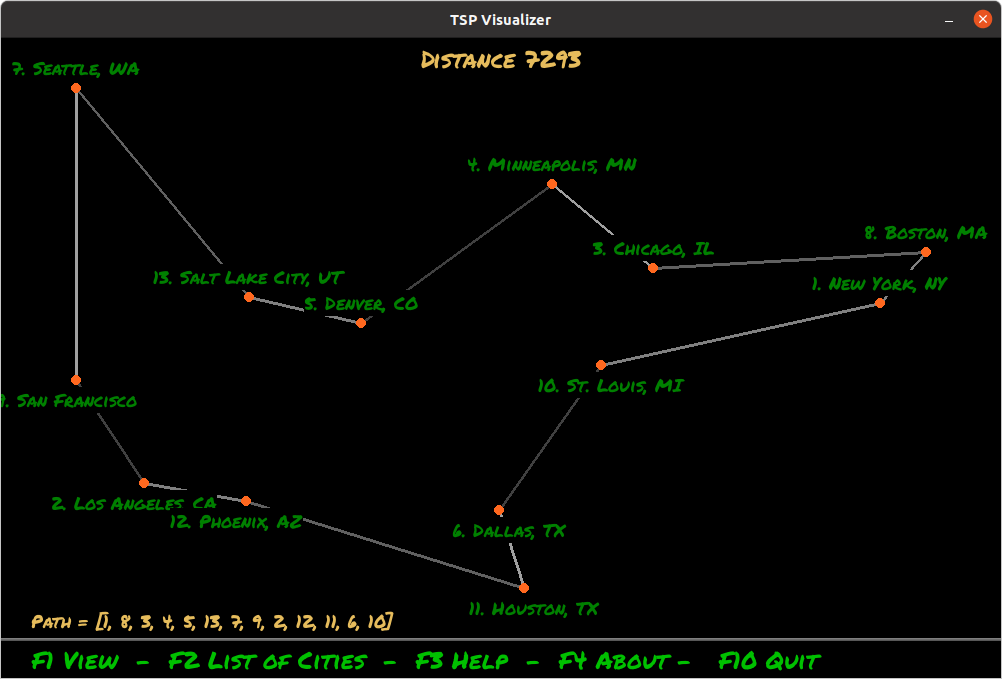
5.3. Visualisation d'un chemin

On peut utiliser le programme python tsp_visualizer.py dont l'implantation se fonde sur l'utilisation de pygame. Il suffit de télécharger l'archive tsp_visualizer.tgz et lancer l'exécution avec le fichier par défaut :

python tsp_visualizer.py tsp_usa_data.txt

Le résultat doit ressembler à l'image suivante :

5.4. Formulation Minizinc

Le programme Minizinc qui permet de résoudre ce problème est le suivant :

tsp.mzn

  1. %% ========================================================
  2. %% Auteur: Jean-Michel Richer
  3. %% email: jean-michel.richer@univ-angers.fr
  4. %% ========================================================
  5. %%
  6. %% Problème du voyageur de commerce
  7. %%    (Travelling Salesman Problem) :
  8. %%
  9. %%    Etant donné N villes pour lesquels on connait les
  10. %%    distances les séparant, trouver un chemin qui ne passe
  11. %%    qu'une seule fois par chaque ville et qui est le plus
  12. %%    court possible.
  13. %%
  14. %%    Le plus court chemin pour cet exemple est 7293.
  15. %%
  16. %% ========================================================
  17.  
  18. include "globals.mzn";
  19.  
  20. %% --------------------------
  21. %%         Variables
  22. %% --------------------------
  23.  
  24. int: N = 13;
  25. array[1..N, 1..N] of int: distances;
  26.  
  27. % cities = [ "1. New York, NY",
  28. %   "2. Los Angeles, CA",
  29. %   "3. Chicago, IL",
  30. %   "4. Minneapolis, MN",
  31. %   "5. Denver, CO",
  32. %   "6. Dallas, TX",
  33. %   "7. Seattle, WA",
  34. %   "8. Boston, MA",  
  35. %   "9. San Francisco, CA",
  36. %   "10. St. Louis, MI",
  37. %   "11. Houston, TX",
  38. %   "12. Phoenix, AZ",
  39. %   "13. Salt Lake City" ]
  40.  
  41. distances = array2d(1..N,1..N,
  42. [
  43.          0, 2451,  713, 1018, 1631, 1374, 2408,  213, 2571,  875, 1420, 2145, 1972,
  44.       2451,    0, 1745, 1524,  831, 1240,  959, 2596,  403, 1589, 1374,  357,  579,
  45.        713, 1745,    0,  355,  920,  803, 1737,  851, 1858,  262,  940, 1453, 1260,
  46.       1018, 1524,  355,    0,  700,  862, 1395, 1123, 1584,  466, 1056, 1280,  987,
  47.       1631,  831,  920,  700,    0,  663, 1021, 1769,  949,  796,  879,  586,  371,
  48.       1374, 1240,  803,  862,  663,    0, 1681, 1551, 1765,  547,  225,  887,  999,
  49.       2408,  959, 1737, 1395, 1021, 1681,    0, 2493,  678, 1724, 1891, 1114,  701,
  50.        213, 2596,  851, 1123, 1769, 1551, 2493,    0, 2699, 1038, 1605, 2300, 2099,
  51.       2571,  403, 1858, 1584,  949, 1765,  678, 2699,    0, 1744, 1645,  653,  600,
  52.        875, 1589,  262,  466,  796,  547, 1724, 1038, 1744,    0,  679, 1272, 1162,
  53.       1420, 1374,  940, 1056,  879,  225, 1891, 1605, 1645,  679,    0, 1017, 1200,
  54.       2145,  357, 1453, 1280,  586,  887, 1114, 2300,  653, 1272, 1017,    0,  504,
  55.       1972,  579, 1260,  987,  371,  999,  701, 2099,  600, 1162, 1200,  504,    0
  56. ]);
  57.  
  58. array[1..N] of var 1..N: x;
  59. int: min_val = min([distances[i,j] | i,j in 1..N where distances[i,j] > 0]);
  60. int: max_val = max([distances[i,j] | i,j in 1..N]);
  61. array[1..N] of var min_val..max_val: d;
  62.  
  63. %% --------------------------
  64. %%        Constraints
  65. %% --------------------------
  66.  
  67. constraint alldifferent(x);
  68. constraint circuit(x);
  69. constraint forall(i in 1..N) (
  70.       distances[i,x[i]] = d[i]
  71.     );
  72.  
  73. %% --------------------------
  74. %%          Search
  75. %% --------------------------
  76.  
  77. var int: distance = sum(d);
  78. solve :: int_search(d, max_regret, indomain_split, complete) minimize distance;    
  79.  
  80. %% --------------------------
  81. %%           Result
  82. %% --------------------------
  83.  
  84. output [
  85.   "x: ", show(x), "\n", show(distance)
  86. ];
  87.  
  88.  
  89.