<< Page principale

3. Optimisation Combinatoire

3.1. Définition

L'Optimisation Combinatoire est une branche de l'optimisation en mathématiques appliquées et en informatique, également liée à la recherche opérationnelle, l'algorithmique et la théorie de la complexité. On parle également d'optimisation discrète car on travaille sur des domaines discrets (non continus).

On cherche la meilleure ou les meilleures solutions d'un problème par rapport à une fonction entière ou réelle appelée fonction de coût, de score ou fonction objectif. On cherche alors à maximiser ou minimiser cette fonction.

Certains problèmes d'optimisation combinatoire peuvent être résolus de manière exacte en temps polynomial par exemple par un algorithme glouton, un algorithme de programmation dynamique ou en montrant que le problème peut être formulé comme un programme linéaire en variables réelles.

Cependant, la majorité de ces problèmes sont NP-complets et pour les résoudre il est nécessaire de faire appel à d'autres techniques, dites heuristiques ou métaheuristiques, afin d'obtenir une solution approchée de manière à garantir l'obtention d'une solution en un temps raisonnable.

3.2. Types de problèmes

On s'intéresse à des problèmes d'optimisation pour lesquels on cherche une solution qui soit la meilleure. Nous allons notamment nous focaliser sur un modélisation sous forme de CSP (Constraint Satisfaction Problems).

On définit un Problème de Satisfaction de Contraintes par :

  • un ensemble de domaines discrets : $D = \{ D_1, D_2, ..., D_n \}$
  • un ensemble de variables $X = \{ x_1, x_2, ..., \x_n \}$, chaque $x_i$ prenant ses valeurs dans $D_i$
  • un ensemble de contraintes $C = \{ C_1, ..., C_m \}$ qui s'expriment entre les variables

On peut augmenter ce cadre théorique avec une fonction objectif (appelée également fonction de coût ou de score) qui permet d'attribuer une valeur de qualité à une instanciation des variables : $$f : D_1 × ... × D_n → ℝ$$.

On peut alors tenter de rechercher la ou les meilleurs solutions par rapport à la fonction objectif. Il s'agit alors d'un problème d'optimisation sous contraintes.

Résoudre un CSP consiste alors :

  • à trouver une instantiation des variables de $X$ qui satisfait les contraintes
  • et dans le cas des CSP avec optimisation, à maximiser (ou minimiser) la fonction objectif $f$

Note : on remarquera que pour certains problèmes il peut y avoir moins de domaines que de variables (cf problème ci-après), les variables prenant généralement leurs valeurs dans un seul domaine.

3.2.1. Exemple SEND + MORE = MONEY

Un cryptarithme ou jeu cryptarithmétique est un casse-tête numérique et logique qui consiste en une équation mathématique où les lettres doivent être remplacées par des chiffres, deux lettres ne pouvant pas avoir la même valeur. L'un des plus connus, car probablement le plus ancien, est le problème $SEND + MORE = MONEY$.

Send+MORE=MONEY

Pour résoudre ce genre de problème il est possible de le formuler comme un CSP :

Notes

il n'est pas nécessaire de définir une fonction objectif, mais elle peut être définie comme étant le nombre de contraintes non satisfaites, on doit donc la minimiser de manière à atteindre 0.

Les contraintes $c_1$ à $c_5$ peuvent être résumées par une seule contrainte :

$$ \table 10000 × M + 1000 × O + 100 × N + 10 × E + Y = ; 1000 × S + 100 × E + 10 × N + D + ; 1000 × M + 100 × O + 10 × R + E ; $$

Dans ce cas, le problème est plus difficile à résoudre car le fait d'avoir plusieurs contraintes permet dès qu'une contrainte est violée de remettre en question les affectations d'un petit nombre de variables.

Résolution

La résolution utilise une méthode exacte pour ce genre de problème :

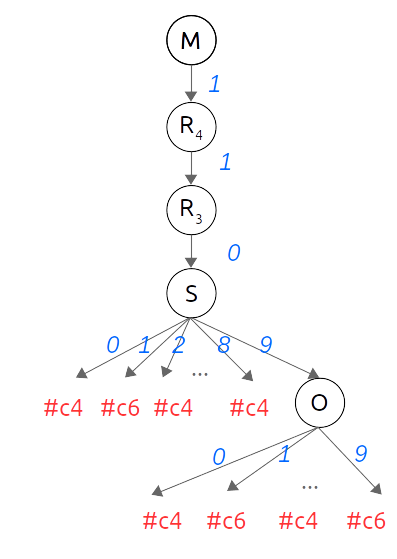
Send+MORE=MONEY résolution

Ce problème peut être résolu efficacement avec un solveur comme Minizinc :

include "globals.mzn";
var 0..9: S;
var 0..9: E;
var 0..9: N;
var 0..9: D;
var 1..9: M;
var 0..9: O;
var 0..9: R;
var 0..9: Y;
var 0..1 : R1;
var 0..1 : R2;
var 0..1 : R3;
var 0..1 : R4;
array[1..8] of var int : letters = [S,E,N,D,M,O,R,Y];

constraint D+E=Y+10*R1;
constraint R1+N+R=E+10*R2;
constraint R2+E+O=N+10*R3;
constraint R3+S+M=O+10*R4;
constraint R4=M;
constraint all_different(letters);
solve satisfy;
output[" \(R4) \(R3) \(R2) \(R1)\n"];
output["   \(S) \(E) \(N) \(D)\n"];
output["   \(M) \(O) \(R) \(E)\n"];
output[" \(M) \(O) \(N) \(E) \(Y)\n"];
output[" SENDMORY = \(all)\n"];

On trouvera de nombreux autres exemples de cryptarithmes sur cette page comme :

Exercice 3.1

Installer Minizinc et résoudre le problème $HUIT + HUIT = SEIZE$.

3.2.2. Exemple les N-Reines

Le problème des N-reines consiste à placer sur un échiquier de $N × N$ cases, $N$ reines de manière à ce qu'aucune reine ne soit en prise avec une autre.

Ce problème a été posé en 1848 par un joueur d'échecs allemand, Max Bezzel, pour $N = 8$.

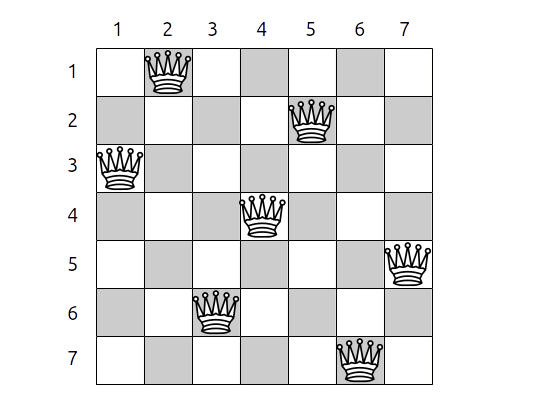
n-reines, n-queens
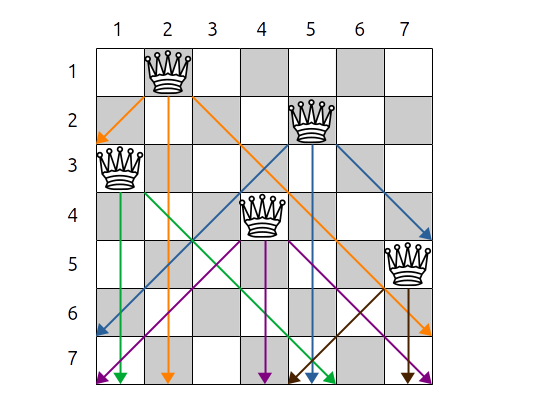
Solution pour N=7
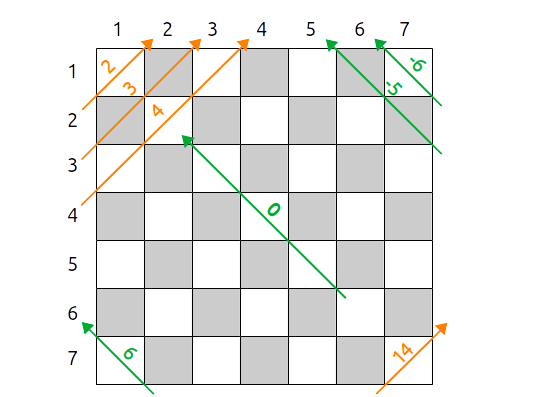
Diagonales droites (orange) et gauches (vert)

Exercice 3.2

Exprimez ce problème sous forme de CSP en déterminant les variables, les domaines et en exprimant les contraintes sur les colonnes et les diagonales. Comment définir la fonction objectif ?

Voici l'expression du problème en Minizinc.

3.3. Méthodes de résolution des CSP

Voici quelques définitions préalables :

Une configuration est une affectation des variables du problème.

Une configuration partielle est une affectation d'une partie des variables du problème.

Une solution est une configuration qui respecte les contraintes du problème.

Toute configuration n'est pas forcément une solution, mais toute solution est une configuration.

L'espace de recherche du problème est l'ensemble des configurations distinctes du problème.

Une solution optimale $X^{⋆}$, également appelée optimum global, est une solution qui vérifie :

  • $f(X^{⋆}) ≥ f(X)$ pour toute solution $X$, s'il s'agit d'un problème de maximisation
  • $f(X^{⋆}) ≤ f(X)$ pour toute solution $X$, s'il s'agit d'un problème de minimisation

Une solution dite optimum local est une solution meilleure que celles qui l'entourent mais moins bonne que l'optimum global.

Plusieurs problèmes emblématiques peuvent être modélisés sous forme de CSP :

3.4. Méthodes exactes ou complètes

Pour résoudre un CSP, on dispose de deux approches :

Avantage

L'intérêt des méthodes exactes est qu'elles vont passer en revue l'ensemble des configurations réalisables du problème et si le problème admet une ou plusieurs solutions optimales, elles seront trouvées.

Inconvénient

Plus le problème est difficile, plus on va prendre de temps pour le résoudre. Certains problèmes sont trop volumineux (nombre de variables, taille des domaines, nombre de contraintes) et demandent trop de calculs pour pouvoir être résolus en un temps raisonnable.

3.4.1. Force brute, énumération exhaustive, recherche arborescente

La méthode la plus simple pour résoudre un problème consiste à réaliser l'énumération de ses configurations, cependant il faut obtenir une configuration qui soit une solution et déterminer si elle est meilleure que celles qu'on a pu trouver précédemment.

La technique arborescente est intéressante car elle permet d'élaguer des branches de l'arbre de recherche et permet ainsi de ne pas passer en revue toutes les configurations existantes.

Certaines techniques dites heuristiques (du grec heuriskô qui signifie "je trouve") ont pour but de mener plus rapidement vers une solution, comme par exemple :

  • l'ordre dans lequel les variables sont affectées
  • l'ordre dans lequel les valeurs sont affectées aux variables

3.4.1.a  Ordre des variables

L'ordre dans lequel on affecte les variables (cf. problème SAT) impacte le temps de résolution de manière importante. Avoir un ordre judicieux permet souvent de gagner beaucoup de temps en évitant les calculs inutiles (cf. problème SAT).

On peut par exemple choisir les variables les plus contraintes (qui participent au plus grand nombre de contraintes, ou appartenant à des contraintes alldiff).

3.4.1.b  Ordre des valeurs du domaine

De la même manière, l'ordre dans lequel on choisit les valeurs à affecter aux variables influe sur le temps de résolution.

On peut alors mettre en oeuvre des techniques de consistance (on parle généralement d'arc-consistance) qui dès qu'on affecte une variable vont chercher les contraintes en relation avec la variable et supprimer des valeurs des domaines des autres variables ou restreindre ces domaines :

L'application de ces règles qui assurent la consistance du problème permettent d'éviter de faire des calculs dont on sait qu'ils ne méneront pas à une solution car les contraintes ne seront pas satisfaites.

3.4.2. Exemple des N-Reines

Reprenons le problème des N-Reines et voyons comment le résoudre par des méthodes exactes :

n-reines, n-queens
Solution pour N=7

Voici le nombre solutions en fonction de $N$ :

 N   Solutions 
 2   0 
 3   0 
 4   2 
 5   10 
 6   4 
 7   40 
 8   92 
 9   352 
 10   724 
 11   2680 
 12   14200 
Problème des N_reines, nombre de solutions

Une configuration du problème peut être représentée sous forme d'un tableau ou d'une liste qui contient la colonne sur laquelle est placée une reine. L'indice du tableau ou de la liste représentant la ligne sur laquelle elle se trouve.

Pour la solution précédente (N=7), on aurait donc $(2,5,1,4,7,3,6)$, l'indice de la première ligne ou colonne commençant à 1 dans ce cas.

3.4.2.a  Enumération exhaustive

On peut résoudre ce problème en réalisant une énumération exhaustive des configurations, il suffit de générer toutes les permutations possibles des valeurs $(1,2, ..., N)$.

Cependant, le nombre de permutations est de l'ordre de $O(n!)$.

 N   Permutations   Solutions   Python   C++ 
 4   24   2   0.00   0.01 
 5   120   10   0.01   0.01 
 6   720   4   0.01   0.01 
 7   5040   40   0.01   0.01 
 8   40320   92   0.08   0.01 
 9   362880   352   0.73   0.15 
 10   3628800   724   7.42   1.77 
 11   39916800   2680   86.97   22.41 
 12   479001600   14200   1095.12   292.28 
 13   6227020800   73712   ?   3984.28 
Résolution du problème des N-reines, nombre de permutations, nombre de solutions, temps de résolution en secondes avec Python et C++ sous AMD Ryzen 5 3600

Voici le code python correspondant :

n_reines_permutations.py

  1. from itertools import permutations
  2. import sys, time
  3.  
  4. nbr_permutations = 0
  5.  
  6. # méthode de résolution
  7. # basée sur les permutations
  8. def resoudre(n):
  9.   global nbr_permutations
  10.   columns = range(n)
  11.   for board in permutations(columns):
  12.     nbr_permutations = nbr_permutations + 1
  13.     s1 = set(board[i] + i for i in columns)
  14.     s2 = set(board[i] - i for i in columns)
  15.     if n == len(s1) == len(s2):
  16.         yield board
  17.      
  18.  
  19. # nombre de reines
  20. N = 8
  21. if len(sys.argv) > 1:
  22.     N = int(sys.argv[1])
  23.  
  24. print("reines=", N)
  25.  
  26. t1 = time.time()
  27. ns = len(list(resoudre(N)))
  28. t2 = time.time()
  29.  
  30. print("permutations=", nbr_permutations)
  31. print("solutions=", ns)
  32. print("temps de calcul=", t2-t1)
  33.  

3.4.2.b  Construction d'une solution

On crée une procédure récursive avec backtrack qui positionne la reine $r$ en colonne $c$ de manière à ce qu'elle ne soit pas en conflit avec une autre reine placée précédemment :

Cependant, on peut envisager différentes solutions pour construire la solution :

Méthode 1

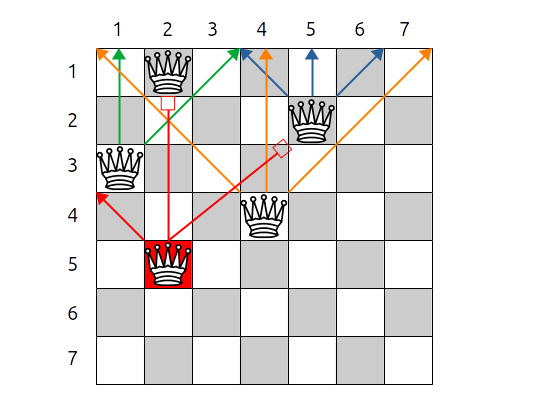
Voici le pseudo code utilisé pour la méthode 1.

n_reines_methode_1.algo

  1. N est un entier // nombre de reines
  2. echiquier est une matrice[1..N][1..N] entier = 0
  3.  
  4. // -------------------------------------------------
  5. // retourne vrai si il existe déjà une reine sur
  6. // la colonne x placée précédemment
  7. // -------------------------------------------------
  8. fonction conflit_colonne(y, x : entier) : booléen
  9.     y2 est un entier = y - 1
  10.     tant que y2 > 0 faire
  11.         si echiquier[ y2 ][ x ] != 0 alors
  12.             retourner vrai
  13.         fin si
  14.         y2 = y2 - 1
  15.     fin tant que
  16.     retourner faux
  17. fin fonction
  18.  
  19. // -------------------------------------------------
  20. // retourne vrai si il existe déjà une reine sur
  21. // la diagonale droite x+y placée précédemment
  22. // -------------------------------------------------
  23. fonction conflit_diag_d(y, x sont des entiers) : booléen
  24.     y2 est un entier = y - 1
  25.     x2 est un entier = x - 1
  26.     tant que y2 > 0 et x2 <= N faire
  27.         si echiquier[ y2 ][ x2 ] != 0 alors
  28.             retourner vrai
  29.         fin si
  30.         y2 = y2 - 1
  31.         x2 = x2 + 1
  32.     fin tant que
  33.     retourner faux
  34. fin fonction
  35.  
  36. // -------------------------------------------------
  37. // retourne vrai si il existe déjà une reine sur
  38. // la diagonale gauche x-y placée précédemment
  39. // -------------------------------------------------
  40. fonction conflit_diag_g(y, x sont des entiers) : booléen
  41.     y2 est un entier = y - 1
  42.     x2 est un entier = x + 1
  43.     tant que y2 > 0 et x2 > 0 faire
  44.         si echiquier[ y2 ][ x2 ] != 0 alors
  45.             retourner vrai
  46.         fin si
  47.         y2 = y2 - 1
  48.         x2 = x2 - 1
  49.     fin tant que
  50.     retourner faux
  51. fin fonction
  52.  
  53. // -------------------------------------------------
  54. // résolution récursive, si il n'existe aucun conflit
  55. // pour placer la reine y dans la colonne x alors
  56. //   on place la reine
  57. //   puis on passe à la suivante
  58. //   on supprime la reine de la position (y,x)
  59. // -------------------------------------------------
  60.  
  61. procedure resoudre(y est un entier)
  62.     si y <= N alors
  63.         pour x de 1 à N faire
  64.             si non(conflit_colonne(y,x) ou conflit_diag_d(y,x)
  65.                 ou conflit_diag_g(y,x)) alors
  66.                 echiquier[y][x] = y
  67.                 resoudre(y + 1)
  68.                 echiquier[y][x] = 0
  69.         fin pour
  70.     sinon
  71.         print("solution")  
  72.     fin si
  73. fin procedure
  74.  
  75.  
  76.  

Méthode 2

Voici le pseudo code utilisé pour la méthode 2.

n_reines_methode_2.algo

  1. N est un entier // nombre de reines
  2. echiquier est une matrice[1..N][1..N] entier = 0
  3.  
  4. // -------------------------------------------------
  5. // remplir dans l'échiquier
  6. // - la colonne x
  7. // - la diagonale droite y+x
  8. // - la diagonale gauche y-x
  9. // -------------------------------------------------
  10. procedure remplir(y, x sont des entiers)
  11.     y2, x2 sont des entiers
  12.    
  13.     // remplir la colonne  
  14.     y2 = y
  15.     x2 = x
  16.     tant que y2 <= N faire
  17.         echiquier[y2][x2] = echiquier[y2][x2] ou_binaire 2^y
  18.         y2 = y2 + 1
  19.     fin tant que
  20.    
  21.     // remplir la diagonale droite
  22.     y2 = y + 1
  23.     x2 = x + 1
  24.     tant que y2 <= N et x2 <= N faire
  25.         echiquier[y2][x2] = echiquier[y2][x2] ou_binaire 2^y
  26.         y2 = y2 + 1
  27.         x2 = x2 + 1
  28.     fin tant que
  29.    
  30.     // remplir la diagonale gauche
  31.     y2 = y + 1
  32.     x2 = x - 1
  33.     tant que y2 <= N et x2 > 0 faire
  34.         echiquier[y2][x2] = echiquier[y2][x2] ou_binaire 2^y
  35.         y2 = y2 + 1
  36.         x2 = x2 - 1
  37.     fin tant que
  38.    
  39. fin procedure
  40.  
  41. // -------------------------------------------------
  42. // même code que remplir sauf qu'il faut supprimer la puissance
  43. // de 2 :
  44. //
  45. //  echiquier[y2][x2] = echiquier[y2][x2] et_binaire non(2^y)
  46. // -------------------------------------------------
  47. procedure effacer(y, x sont des entiers)
  48.  ...
  49. fin procedure
  50.  
  51. // -------------------------------------------------
  52. // Résolution récursive
  53. // -------------------------------------------------
  54. procedure resoudre(y est un entier)
  55.     si y <= N alors
  56.         pour x de 1 à N faire
  57.             si echiquier[y][x] = 0 alors
  58.                 remplir(y,x)
  59.                 resoudre(y + 1)
  60.                 effacer(y,x)
  61.             fin si
  62.         fin pour
  63.     sinon
  64.         print("solution")  
  65.     fin si
  66. fin procedure
  67.  
  68.  

Méthode 3

On utilise trois tableaux d'entiers initialisés à 0 :


Diagonales droites (orange) et gauches (vert)

Voici le pseudo code utilisé pour la méthode 3.

n_reines_methode_3.algo

  1. colonnes est en tableau [1..N] entier = 0
  2. diag_droite est un tableau [2..2*N] entier = 0
  3. diag_gauche est un tableau [-(N-1) .. (N-1)] entier = 0
  4.  
  5. procedure resoudre(y est un entier)
  6.     si y <= N alors
  7.         pour i de 1 à N faire
  8.             si (colonnes[i] = 0) et (diag_droite[y+i] = 0)
  9.                 et (diag_gauche[y-i] = 0) alors
  10.                 colonnes[i] = y
  11.                 diag_droite[y+i] = y
  12.                 diag_gauche[y-i] = y
  13.                 resoudre(y+1)
  14.                 colonnes[i] = 0
  15.                 diag_droite[y+i] = 0
  16.                 diag_gauche[y-i] = 0               
  17.             fin si
  18.         fin pour
  19.     sinon
  20.         print("solution")
  21.     fin si
  22. fin procedure
  23.  

Résultats

Les résultats présentés dans la table suivante montrent l'efficacité des trois méthodes.

 N   Méthode 1   Méthode 2   Méthode 3 
 8   0.00   0.00   0.00 
 9   0.00   0.00   0.00 
 10   0.00   0.00   0.00 
 11   0.00   0.00   0.00 
 12   0.04   0.00   0.00 
 13   0.24   0.03   0.02 
 14   1.46   0.22   0.15 
 15   9.37   1.41   1.03 
 16   64.19   9.31   7.20 
 17   462.73   64.69   54.12 
Résolution du problème des N-reines sur AMD Ryzen 5 3600 en C++

La méthode trois qui utilise trois tableaux pour indiquer si une reine est dans une colonne, une diagonale droite ou une diagonale gauche, est la plus efficace.

Voici le code minizinc du problème des N-Reines :

include "globals.mzn";
int: N = 8;
array[1..N] of var 1..N: queens;

constraint alldifferent(queens);

constraint alldifferent([ queens[i] + i | i in 1..N]); % distinct diagonals
constraint alldifferent([ queens[i] - i | i in 1..N]); % upwards+downwards

% search
solve satisfy;

output [ if fix(queens[j]) == i then "Q" else "." endif ++
         if j == N then "\n" else "" endif | i,j in 1..N]

3.5. Méthodes inexactes, incomplètes ou approchées

Certaines instances de problèmes peuvent demander des siècles voire des millions ou milliards d'années pour être résolues par des approches exactes.

On décide alors de tenter de trouver une solution sous-optimale (que l'on espère proche de l'optimum global) en passant moins de temps à chercher mais en cherchant intelligemment.

Avantage

On ne s'intéresse qu'à une partie des configurations réalisables du problème, on mettra donc généralement moins de temps à résoudre le problème qu'avec une méthode exacte.

Inconvénient

On risque de ne pas trouver la ou les solutions optimales mais une ou des solutions approchées (sous optimales). Au final on ne sait pas si la solution trouvée est la solution optimale.

Ces méthodes sont souvent qualifiées de métaheuristiques. Une métaheuristique est un algorithme d’optimisation visant à résoudre des problèmes d'optimisation considérés comme difficiles.

On peut classer les métaheuristiques en grands groupes ou suivant leurs caractéristiques sachant qu'on peut également intégrer tel ou tel aspect d'une métaheuristique dans une autre métaheuristique :

3.5.1. La recherche locale (Local Search)

Les méthodes fondées sur la recherche locale se basent sur la notion de voisinage d'une configuration.

Partant d'une configuration $X$, on définit par exemple les voisins ou le voisinage $N(X)$ de $X$ comme étant toutes les configurations $X'$ pour lesquelles on a modifié la valeur d'une des variables $x_i$.

On s'arrange pour que le voisinage soit inclus strictement dans l'ensemble des configurations et/ou qu'il soit plus petit que l'ensemble des configurations possibles.

La taille du voisinage va donc influer sur la recherche : plus le voisinage est grand, plus on pourra explorer d'espace de recherche, mais plus la recherche prendra du temps.

Le principe de la recherche locale également appelée descente ou hill-climbing consiste, partant d'une configuration donnée, à rechercher les voisins améliorants et à en choisir un parmi ceux existants. On s'arrête si on ne trouve pas de voisin améliorant.

  1. // cas d'un problème de maximisation
  2. // configuration courante
  3. X_c = configuration
  4.  
  5. // indicateur de poursuite de la recherche
  6. // s'il est faux alors il n'y a plus de voisin améliorant
  7. continuer = vrai
  8.  
  9. // tant qu'il existe un voisin améliorant, le choisir
  10. tant que continuer faire
  11.  
  12.   voisins_ameliorants = { }
  13.  
  14.   // rechercher les voisins améliorants
  15.   pour tout X_n appartenant à N(X_c) faire
  16.     si f(X_n) > f(X_c) alors
  17.       voisins_ameliorants.ajouter( X_n )
  18.     fin si
  19.   fin pour
  20.  
  21.   // si pas de voisin améliorant, s'arrêter
  22.   si voisins_ameliorants.est_vide() alors
  23.     continuer = faux
  24.   sinon
  25.     // sinon choisir un voisin améliorant
  26.     // qui devient la solution courante
  27.     X_a = voisins_ameliorants.selection()
  28.     X_c = X_a
  29.   fin si
  30.  
  31. fin tant que
  32.  

La recherche locale n'est généralement pas assez puissante et plusieurs problèmes se posent alors :

  1. on peut faire un mauvais choix de voisin (si il y en a plusieurs) et s'orienter vers un chemin qui ne permet pas d'atteindre la solution optimale
  2. la solution optimale peut ne pas être sur un chemin améliorant
  3. on peut être bloqué dans un optimum local

Voici une représentation explicative à une dimension mais il faut bien comprendre que l'on travaille en $n$ dimensions et que les courbes ne sont pas lisses.

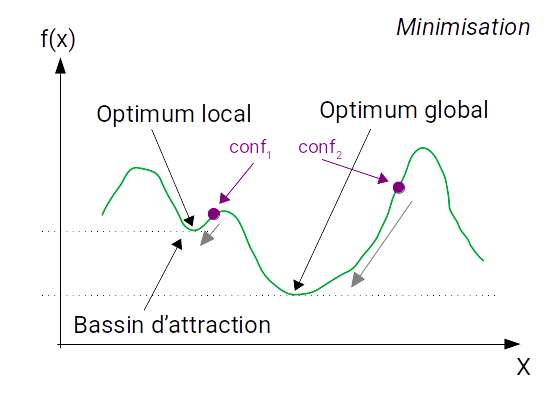
descente

Autre exemple :

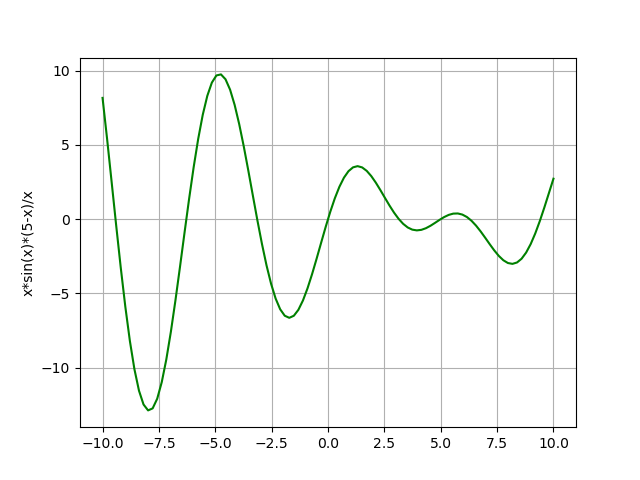
x*sin(x)*(5-x)/x

Plusieurs variantes de la recherche locale existent :

Les problèmes liés aux méthodes inexactes et métaheuristiques qui en découlent sont liés à l'intensification et la diversification qui sont deux notions complémentaires et contradictoires :

  • l'intensification consiste à se focaliser sur une configuration intéressante et à intensifier la recherche autour de cette configuration afin de trouver un meilleur voisin
  • la diversification consiste à ne pas focaliser sa recherche autour d'une configuration mais à trouver des voisins plus prometteurs en explorant un plus grand espace de recherche

3.5.2. Recherche Locale Itérée (Iterated Local Search)

La recherche locale itérée consiste à lancer plusieurs fois une recherche locale en partant d'une une nouvelle solution à chaque étape. On gardera la meilleure solution obtenue.

3.5.3. Algorithme glouton (Greedy algorithm)

Le principe de l'algorithme glouton consiste à faire à chaque étape un choix optimum local dans l'espoir d'obtenir un résultat optimum global.

En d'autres termes, on cherche à chaque étape à faire le choix de la minimisation (ou de la maximisation) lors du choix d'une valeur à affecter à une variable.

Cette technique n'est probante que sur des problèmes simples, néanmoins elle peut être utilisée afin de construire une configuration initiale avant de lancer une descente ou une autre metaheuristique.

3.5.4. La recherche Tabou (Tabu Search)

La recherche tabou se fonde sur un mécanisme de mémorisation des configurations déjà visitées afin d'éviter de boucler. Ce mécanisme de mémorisation est appelée liste tabou. En fait il s'agit d'une liste de taille fixe et le fait d'ajouter un nouvel élément en fin de liste supprime l'élément le plus ancien en début de liste.

  1. $X_0$ = génerer une solution initiale
  2. $X_m$ = $X_0$
  3.  
  4. liste_tabou = []
  5.  
  6. while condition_d_arrêt non vérifiée faire
  7.   $X_t$ = descente($X_c$, $N$)
  8.   si $X_t  ∉$ liste_tabou alors
  9.     if f($X_t$) < f($X_m$) alors
  10.       $X_m$ = $X_t$
  11.     fin si
  12.     $X_c$ = $X_t$
  13.     liste_tabou.ajouter_en_fin($X_c$)
  14.   fin si
  15. fin tant que
  16.  

3.5.5. Le recuit-simulé (Simulated Annealing)

Le recuit simulé (Simulated Annealing) est une métaheuristique basée sur le travail de Metropolis (). Elle se fonde sur une analogie avec le recuit en métallurgie qui consiste par exemple à refroidir un alliage de manière progressive afin de lui conférer des propriétés autres que celles que l'on aurait obtenu avec un refroidissement brutal.

Le recuit simulé est une descente avec un probabilité d'accepter des solutions moins bonnes avec un facteur de probabilité (règle de Metropolis) qui décroit à mesure que le système se refroidit.

  1. $X_0$ = solution initiale
  2. $T_0$ = température initiale
  3. $T_f$ = température finale
  4. $α$ = facteur de refroidissement
  5.  
  6. // on fixe la température courante
  7. $t$ = $T_0$
  8. $X_c$ = $X_0$
  9. // meilleure solution
  10. $X_m$ = $X_0$
  11.  
  12. iteration = 1
  13. tant que $t ≠ T_f$ faire
  14.   $X_v$ = generer_un_voisin( $X_c$, iteration, $N$ )
  15.   $Δ_f$ = f($X_v$) - f($X_c$)
  16.   $u$ = valeur aléatoire entre [0,1]
  17.   si ($Δ_f$ < 0) ou (exp(-Δ_f / t) > $u$) alors
  18.     $X_c$ = $X_v$
  19.   fin si 
  20.   // garder la meilleure solution
  21.   si f($X_c$) < f($X_m$) alors
  22.     $X_m$ = $X_c$
  23.   fin si
  24.    
  25.   iteration = iteration + 1
  26.   $t$ = $α × t$
  27. fin tant que
  28.  
  29. retourner $X_m$
  30.  

La difficulté de la méthode repose sur les paramètres qui doivent être déterminés de manière empirique :

Lien

3.5.6. Les algorithmes génétiques (Genetic Algorithms)

Les algorithmes génétiques comme leur nom l'indique se base sur la génétique et la reproduction cellulaire. Ils font partie des algorithmes à population et des algorithmes évolutionnaires c'est à dire qu'ils s'inspirent de la théorie de l'évolution.

On part d'un ensemble de configurations initiales qui constituent la population $P$. Cette population évolue au cours des générations. A chaque génération :

  • on choisit deux individus (configurations) de la population $X_p$ le père et $X_m$ la mère
  • on mixe ces deux solutions pour enfanter une nouvelle configuration $X_e$ (croisement - crossover)
  • on soumet $X_e$ à une ou plusieurs mutations
  • on évalue alors le nouvel individu et s'il est meilleur que l'un de ses deux parents il est ajouté à la population $P$ alors que le parent le moins bon comparativement à $f$ est supprimé de $P$ ou alors on élimine l'individu de la population qui est le moins bon

On pratique en quelque sorte un eugénisme.

  1. $P$ = ensemble de configurations
  2. $G$ =  500 // nombre maximum de générations
  3.  
  4. pour generation de 1 à $G$ faire
  5.   // choisir un père et une mère
  6.   $X_p$, $X_m$ = choisir deux configurations distinctes dans $P$
  7.  
  8.   // générer un enfant par croisement
  9.   $X_e$ = croisement($X_p$, $X_m$)
  10.  
  11.   // appliquer une mutation chez l'enfant
  12.   $X_e$ = mutation($X_e$)
  13.  
  14.   // remplacer le père ou la mère par l'enfant si ce dernier
  15.   // est meilleur que l'un de ses deux parents
  16.   remplacement(P, $X_p$, $X_m$, $X_e$)
  17.  
  18. fin pour
  19.  

Le problème que l'on peut rencontrer, dû à l'eugénisme, est le fait qu'après un certain temps les individus peuvent être similaires ce qui empêche la recherche de trouver des solutions plus intéressantes.

Plusieurs variantes de cet algorithme existent : on peut par exemple générer plusieurs enfants, choisir non pas deux mais plusieurs parents et les combiner.

3.5.7. Les algorithmes mémétiques (Memetic Algorithms)

Un algorithme mémétique est simplement un algorithme génétique pour lequel on applique une descente sur l'enfant généré à partir des deux parents après mutation.

On va donc chercher à obtenir un enfant bien meilleur que ses parents.

3.5.8. Autres algorithmes et techniques

Il existe de nombreux autres algorithmes dont beaucoup sont inspirés de la nature comme :

Certaines techniques peuvent être développées pour des problèmes particuliers :

3.5.8.a  Les algorithmes à colonies de fourmis (Ant Colony Optimzation)

On se base sur le comportement des fourmis qui recherchent de la nourriture. La nourriture étant ici une bonne solution.

On dispose d'une population de fourmis qui construisent des solutions et déposent sur les voies qu'elles empruntent des phéromones. Plus il y a de phéromones sur une voie, plus il y a de chance qu'il s'agissent d'un chemin qui mène à une bonne solution.

Cette technique est bien adaptée au problème du voyageur de commerce (cf. Wikipedia.

3.5.8.b  Les algorithmes à Essaims Particulaires (Particle Swarm Optimization)

Les algorithmes à Essaims Particulaires reposent sur le principe d'auto-organisation d'un groupe d'organismes vivants (notamment les oiseaux) d'agir ensemble et d'exhiber un comportement complexe, à partir de comportements simples des individus, en respectant les règles suivantes :

On pourra lire l'article suivant PSO (de Data Analytics Post) pour de plus amples explications.