<< Page principale
2. Le problème SAT
2.1. Définitions
Le problème de SATisfaisabilité (ou de satisfiabilité, hérité de l'anglais) d'un ensemble de clauses propositionnelles consiste à trouver une affectation des variables logiques propositionnelles qui fasse en sorte que toutes les clauses soient interprétées à vrai.
Ce problème est l'archétype des problèmes NP-Complets.
Pour $n$ variables, il existe $2^n$ configurations dont une partie (ou aucune) est solution du problème et on ne connaît pas d'algorithme polynomial qui permettrait d'atteindre une solution.
$$ \table \text"Configuration", x_1, x_2, ..., x_{n-1}, x_n ; 0, 0, 0, ..., 0, 0; 1, 0, 0, ..., 0, 1; 2, 0, 0, ..., 1, 0; ... ; 2^{n}-1, 1, 1, ..., 1, 1; $$Si le problème ne possède pas de solution, il faudra alors tester toutes les configurations possibles et montrer qu'elles sont toutes insatisfiables (insatisfaisables) pour démontrer que le problème est inconsistant (insatisfiable).
Par exemple, si $n = 64$, alors $2^n = 1,8 × 10^{19}$. Si on pouvait générer et tester une configuration en 1 ns (ce qui serait très efficace), il faudrait $1,8 × 10^{10}$ secondes pour résoudre le problème soit environ 584 ans sur une seule machine.
2.2. Rappels de logique
On rappelle qu'une clause est une disjonction de littéraux de la forme :
$$ (c_1) \text" " x_1 ∨ ¬ x_2 ∨ … ∨ ¬ x_i $$Un problème exprimé sous forme normale conjonctive (CNF) est une conjonction de disjonctions :
$$ ⋀↙{i=1}↖{k} ( ⋁↙{j=1}↖{j_k} l_j ) $$où $l_j$ est un littéral de la forme $x_i$ ou $¬ x_i $.
- le symbole $∧$ représente la conjonction (le ET logique)
- le symbole $∨$ représente la disjonction (le OU logique)
- le symbole $¬$ représente la négation (le NON logique)
Exemple
Considérons le problème suivant :
- s'il fait beau ou il n'y a pas de vent alors je fais du vélo
- il fait beau
Peut on en déduire si je fais ou non du vélo ?
Pour cela, on modélise le problème en remplaçant les expressions par des variables propositionnelles :
- $x_1 =$ il fait beau
- $x_2 =$ il y a du vent
- $x_3 =$ je fais du vélo
Le problème s'exprime alors sous forme logique par :
- $(x_1 ∨ ¬ x_2) → x_3$
- $x_1$
Or, une expression de la forme $X → Y$ est équivalente à $¬X ∨ Y$. La première expression donne alors :
$$ ¬(x_1 ∨ ¬ x_2) ∨ x_3 \;\;\;\; ⇒ \;\;\;\; (¬x_1 ∧ x_2) ∨ x_3 \;\;\;\; ⇒ \;\;\;\; (¬x_1 ∨ x_3) ∧ (x_2 ∨ x_3) $$Le problème est au final représenté sous forme CNF par 3 clauses :
$$ (¬x_1 ∨ x_3) ∧ (x_2 ∨ x_3) ∧ (x_1) $$ $$ \{\table (c_1) , ¬x_1 ∨ x_3; (c_2), x_2 ∨ x_3; (c_3), x_1; $$Dès lors, on peut résoudre le problème de deux manières différentes :
- soit en ajoutant la négation de la conclusion (que l'on tente de démontrer) et en prouvant l'inconsistance ($H ∧ ¬C → ⊥$)
- soit en trouvant une instanciation du problème qui montre la consistance
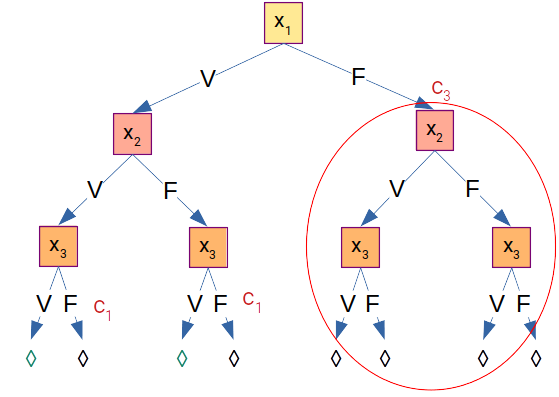
Si on choisit la seconde solution, on doit rendre vraies les clauses $(c_1)$, $(c_2)$, $(c_3)$. On obtient l'une des résolutions suivantes :
- pour la première (celle de gauche), l'ordre de résolution des variables est $x_1, x_2, x_3$
- pour la seconde (celle de droite), l'ordre de résolution des variables est $x_1, x_3, x_2$
Dans les deux cas, on obtient les mêmes solutions :
Comme $x_3 = V$ dans les deux cas, on en déduit que l'on fait du vélo.
Exercice 2.1
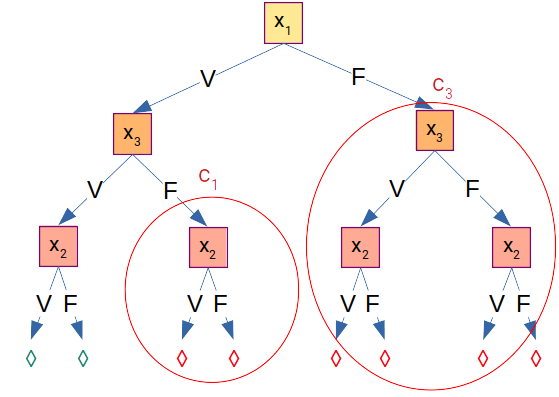
Reprendre l'exercice et démontrer l'inconsistance si on ajoute la négation de la conclusion, soit $¬ x_3$, à l'ensemble de clauses précédentes. On a donc :
$$ \{\table (c_1) , ¬x_1 ∨ x_3; (c_2), x_2 ∨ x_3; (c_3), x_1; (c4), ¬x_3 ; $$Ces deux résolutions font apparaître deux choses importantes :
- il n'est pas nécessaire de générer certaines configurations puisque l'instanciation de certaines variables falsifie certaines clauses (cas de $x_1 = V$ et $x_3 = F$ pour (c_1)$
- l'ordre dans lequel on instancie les variables possède une influence sur le temps de résolution puisqu'il permettra d'éliminer plus ou moins rapidement certaines branches de l'arbre de résolution : notamment, ici il faut commencer avec les clauses les plus petites comme $(c_3)$ et poursuivre avec les clauses qui contiennent des variables déjà instanciées comme $(c_1)$, après avoir instancié $x_1$ de $(c_3)$
Comme nous le verrons plus tard, une méthode de force brute (brute force) va générer et tester toutes les configurations. Une méthode plus intelligente va tenter de construire une configuration qui satisfasse les clauses à mesure que l'on instancie des variables (recherche arborescente avec retour arrière).
2.3. Algèbre de Boole
Nous allons montrer qu'on peut utiliser une autre approche que celle de la logique pour créer un problème de satisfaction de contraintes (CSP), dont nous reparlerons plus en détail dans le chapitre suivant.
L'algèbre de Boole, du nom du mathématicien, logicien et philosophe britannique George Boole (1815-1864), est une partie des mathématiques qui s'intéresse à une approche algébrique de la logique, alors que la logique se fonde sur des systèmes de réécriture qui consistent à manipuler des symboles. La logique possède bien évidemment un volet sémantique et l'algèbre de Boole vient renforcer la sémantique logique en remplaçant le vrai et le faux par le 1 et le 0, le et et le ou par les opérateurs $+$ et $.$ (addition et multiplication).
Cette vision arithmétique de la logique a permis de mettre au point un système de calcul qui possède des applications dans la mise au point de circuits électroniques et autorise à aborder les problèmes de la logique sous un angle différent, ce qui peut, dans certains cas, donner la possibilité de résoudre un problème beaucoup plus simplement ou rapidement. Nous allons l'expérimenter sur le problème des pigeons.
2.4. Définitions
Soit un ensemble $\sc A = \{ 0, 1 \}$ pour lequel on a $0 ≤ 1$. On définit alors les opérations suivantes sur $\sc A$
- l'addition : $a + b$ dont la sémantique est $max(a,b)$
- la multiplication : $a . b = min(a,b)$
- la complémentation : $\ov 0 = 1$ et $\ov 1 = 0$
Une variable complémentée $\ov x$ est également dite signée ou négative.
Le résultat des opérations $+$ et $.$ apparaît ci-dessous d'après la sémantique que nous avons donnée.
| a | b | a + b | a.b |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
Le quadruplet $({\sc A,+,.,\ov x)$ est appelé algèbre de Boole s'il respecte les axiomes suivants :
- l'addition et la multiplication sont commutatives et associatives : $$ \table a + b ,=, b + a; a . b ,=, b . a; (a + b) + c ,=, a + (b + c); (a . b) . c = a . (b . c); $$
- $0$ est élément neutre pour l'addition et $1$ est élément neutre pour la multiplication : $$ \table 0 + a ,=, a ; 1 . a ,=, a ; $$
- l'addition et la multiplication sont distributives l'une par rapport à l'autre : $$ \table (a + b) . c ,=, a . c + b . c; (a . b) + c ,=, (a + c) . (b + c); $$
- la complémentation est telle que $\ov {\; \ov a \;} = a$ et vérifie les propriétés suivantes : $$ \table a + \ov a ,=, 1 ; a . \ov a ,=, 0 ; $$
Si l'on rapporte ces opérations à la logique, alors :
- $1$ indique le caractère vrai d'une propriété ou d'un énoncé
- $0$ indique le caractère faux
- l'addition ($+$) correspond au ou
- la multiplication ($.$) correspond au et
- la complémentation $\ov a$ correspond à non (noté $¬$ en logique), i.e. le contraire de $a$
Ainsi, l'expression $a + \ov a = 1$ peut s'interpréter : dire qu'une chose est vraie ou n'est pas vraie est toujours vrai. Je peux par exemple remplacer $a$ par l'énoncé il pleut, et donc, dans ce cas, il est vrai que : il pleut ou il ne pleut pas.
De la même manière $a . \ov a = 0$ signifie qu'on ne peut pas dire une chose et son contraire. Je ne peux pas à la fois être grand et ne pas être grand.
C'est grâce à cette modélisation de la logique sous forme d'opérations arithmétiques que l'on peut simplifier certains traitements modélisés sous forme de fonctions booléennes.
2.4.1. Le problème des pigeons
Le problème des pigeons est un problème logique très simple à concevoir de mise en correspondance. Nous allons le modéliser sous forme logique avant de basculer vers l'algèbre de Boole et l'algèbre classique.
Problème des pigeons
Etant donné $n$ pigeons et $q$ pigeonniers, chaque pigeon devant trouver un pigeonnier et un pigeonnier ne pouvant accueillir qu'au maximum un seul pigeon, restera t-il des pigeons sans pigeonnier ? Où, en d'autres termes, chaque pigeon trouvera t-il un pigeonnier ?
Il est évident pour un cerveau humain que si $n ≤ q$, le problème possède des solutions et il n'en possède pas dès lors que $p > q$.
Pour modéliser le problème en logique propositionnelle, il faut utiliser un ensemble de variables propositionnelles et exprimer des clauses entre les variables.
On utilisera une matrice de $n × q$ variables propositionnelles pour représenter le problème des pigeons : $$ X(n,q) = [\table x_1^1 , x_1^2 , ⋯ , x_1^q ; x_1^2 , x_2^2 , ⋯ , x_2^q ; ⋮ , , , ⋮ ; x_n^1 , x_n^2 , ⋯ , x_n^q ; ] $$
Si la variable $x_i^j$ est à vrai cela signifie que le pigeon $i$ est dans le pigeonnier $j$. Cela implique donc que les variables $x_i^1, ..., x_i^{j-1}, x_i^{j+1}, ..., x_i^{q}$ sont à faux. En d'autres termes, le pigeon étant dans le pigeonnier $j$, il ne peut pas être dans les autres pigeonniers.
On doit donc exprimer deux types de contraintes :
- contrainte de type $Ctr_L$ (sur les lignes) : un pigeon est dans un et un seul pigeonnier
- contrainte de type $Ctr_C$ (sur les colonnes) : un pigeonnier contient au plus un pigeon, il peut donc ne pas en contenir si $n < q$
Dans le cas ou $n=3$ et $q=3$, le problème est modélisé comme suit, on renomme les variables afin de faciliter l'écriture des clauses :
$$ X(3,3) = [ \table a , b , c ; d , e , f ; g , h , i ; ] = [ \table x_1^1 , x_1^2 , x_1^3; x_2^1 , x_2^2 , x_2^3; x_3^1 , x_3^2 , x_3^3; ] $$- le pigeon 1 est dans un seul pigeonnier (4 clauses) : $$ \table a ∨ b ∨ c ; ¬ a ∨ ¬ b ; ¬ a ∨ ¬ c ; ¬ b ∨ ¬ c ; $$
- le pigeon 2 est dans un seul pigeonnier (4 clauses): $$ \table d ∨ e ∨ f ; ¬ d ∨ ¬ e ; ¬ d ∨ ¬ f ; ¬ e ∨ ¬ f ; $$
- le pigeon 3 est dans un seul pigeonnier (4 clauses): $$ \table g ∨ h ∨ i ; ¬ g ∨ ¬ h ; ¬ g ∨ ¬ i ; ¬ h ∨ ¬ i ; $$
- le pigeonnier 1 contient au plus un pigeon (3 clauses): $$ \table ¬ a ∨ ¬ d ; ¬ a ∨ ¬ g ; ¬ d ∨ ¬ g ; $$
- le pigeonnier 2 contient au plus un pigeon (3 clauses): $$ \table ¬ b ∨ ¬ e ; ¬ b ∨ ¬ h ; ¬ e ∨ ¬ h ; \end{array} $$
- le pigeonnier 3 contient au plus un pigeon (3 clauses): $$ \table ¬ c ∨ ¬ f ; ¬ c ∨ ¬ i ; ¬ f ∨ ¬ i ; $$
Soit un total de 21 clauses pour $n=3$ et $q=3$.
Le nombre de clauses générées est défini par la formule :
$$ n × ( 1 + ∑↙{i=1}↖{q-1} i ) + q × ( ∑↙{i=1}↖{n-1} i ) $$Si $n = q = 10$, on génère $910$ clauses.
2.4.2. Résolution du problème en logique
Pour résoudre ce problème en logique il faut utiliser un solveur ou un démonstrateur automatique de théorème comme Otter (Organized Techniques for Theorem-proving and Effective Research, [2]).
La méthode qui permet de résoudre le problème sous forme de clauses consiste à appliquer la règle dite du Principe de Résolution définie par John Alan Robinson [3].
A partir d'une clause qui possède une variable propositionnelle $p$ et une autre clause qui possède la variable sous forme négative ($¬ p$), on génère une nouvelle clause :
$$ {\cl"green"{p} ∨ L \;\;\;\;\;\; \cl"green"{¬p} ∨ M}/{ L ∨ M } $$$L$ et $M$ étant des variables propositionnelles séparées par le symbole $∨$.
On applique cette règle entre toutes les clauses quand cela est possible. On va donc générer un ensemble de plus en plus important de clauses à mesure que le nombre de pigeons et de pigeonniers augmentent. Les nouvelles clauses ajoutées à l'ensemble initial seront utilisées pour générer encore plus de clauses. Il se peut que l'on génère plusieurs fois la même clause, dans ce cas, si elle existe déjà, on ne l'ajoutera pas. On n'ajoutera pas également les tautologies qui sont de la forme $¬p ∨ p$, car dans ce cas $¬p ∨ p = 1$, il en résulte alors que $1 ∨ L = 1$.
On terminera dans les deux cas suivants :
- soit le problème possède des solutions, on dit qu'il est satisfiable (ou consistant), et arrivera un moment ou on ne générera pas de nouvelle clause
- soit le problème n'a pas de solution, il est insatisfiable (ou inconsistant), et on génèrera la clause vide : $$ {p \;\;\;\;\; ¬p}/{ ⊥ } $$
Si le problème est insatisfiable c'est qu'on a pu générer à partir d'un sous-ensemble de clauses la clause qui se résume à un seul littéral $p$, et qu'à partir d'un autre sous-ensemble on a généré son contraire. Le problème est donc insatisfiable car on ne peut affirmer une chose et son contraire.
Par exemple dans le cas ou $p=3$ et $q=2$, le problème n'a pas de solution et la résolution se fait en 18 étapes. Voici la preuve trouvée par Otter :
---------------- PROOF ----------------
4 [] -p1_1| -p2_1.
5 [] -p1_1| -p3_1.
6 [] -p2_1| -p3_1.
7 [] -p1_2| -p2_2.
8 [] -p1_2| -p3_2.
9 [] -p2_2| -p3_2.
10 [] p1_1|p1_2.
11 [] p2_1|p2_2.
12 [] p3_1|p3_2.
13 [hyper,11,7,10] p1_1|p2_1.
14 [hyper,12,9,11] p2_1|p3_1.
15 [hyper,12,8,10] p1_1|p3_1.
16 [hyper,15,6,13] p1_1.
17 [hyper,16,5,14] p2_1.
18 [hyper,17,4,16] $F.
Les variables $x_i^j$ sont renommées en pi_j car Otter considère que le symbole x est une variable du calcul des prédicats et non une variable du calcul propositionnel.
Otter utilise ici une règle appelée hyper-résolution (HR) qui est dérivée du Principe de Résolution et on génère la clause vide, matérialisée par \$F. Par exemple, la clause 13 est obtenue par :
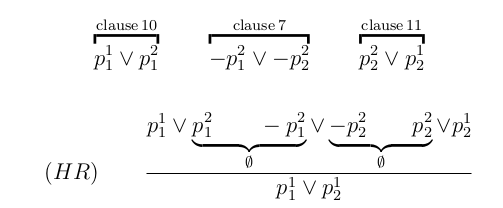
A mesure que $p$ et $q$ augmentent, le nombre de clauses augmente et la résolution prend plus de temps. Si on prend $p=5$ et $q=4$, Otter prouvera qu'il n'y a pas de solution en 142 étapes.
2.4.3. Modélisation sous forme de contraintes de cardinalité
Pour résoudre plus simplement ce problème, on peut le modéliser sous un autre formalisme qui utilise des contraintes de cardinalité, opérateur introduit dans le cadre de la Programmation Logique avec Contraintes par Pascal Van Hentenryck et Yves Deville en 1991 [4].
Nous utilisons ici une variante de l'opérateur pour la logique :
$$ \#(α, β, \{ L \} )$$où $α$ et $β$ sont des entiers positifs ou nuls tels que $0 ≤ α ≤ β$ et $L$ est une liste de variables booléennes.
La contrainte signifie qu'au minimum $α$ et au plus $β$ variables de $L$ sont vraies.
On modélise alors le problème par une matrice de variables booléennes $X(n,q)$, telles que $x_i^j = 1$ signifie que le pigeon $i$ est dans le pigeonnier $j$.
Le problème des pigeons s'exprime alors par deux types de contraintes :
- un pigeon est dans un et un seul pigeonnier (contrainte de type $Ctr_L$) : $$ \{ \table \#(1,1, \{ x_1^1, ..., x_1^q \} ) ; ... ; \#(1,1, \{x_n^1, ..., x_n^q \}) ; $$
- un pigeonnier accueille au plus un pigeon (contrainte de type $Ctr_C$) : $$ \{ \table \#(0,1, \{x_1^1, ..., x_n^1\}) ; ... ; \#(0,1, \{x_1^q, ..., x_n^q\}) ; $$
2.4.4. Résolution avec des contraintes de cardinalité
On peut vérifier la consistance (ou l'inconsistance) du problème en utilisant un système de déduction comme celui de [1] (cf. pages 80 et 81). On utilise la règle d'extension $(Ext)$ définie ainsi :
$$ {\#(α_1, β_1, \{ L_1 \}) \;\;\;\; \#(α_2, β_2, \{ L_2 \}) } / { \#(α_1 + α_2, β_1 + β_2, \{ L_1 ∪ L_2\})} $$On remplace deux contraintes de cardinalité par une seule en faisant en quelque sorte la somme des deux contraintes initiales. Pour cela, il est généralement préférable de faire en sorte que $L_1 ∩ L_2 = ∅$.
Si on applique la règle $(Ext)$ sur l'ensemble des contraintes liées à $Ctr_L$, puis sur l'ensemble des contraintes liées à $Ctr_C$, on obtient respectivement :
- un pigeon est dans un et un seul pigeonnier $Ctr_L$ : $$\#(n,n, \{ X(n,q) \} )$$
- un pigeonnier accueille au plus un pigeon $Ctr_C$ : $$\#(0,q, \{ X(n,q) \} )$$
Le problème se résume donc à ces deux contraintes.
La règle d'inconsistance $(Inc_1)$ permet de déduire rapidement si le problème possède ou pas une solution. Cette règle stipule que si on dispose de deux contraintes de cardinalité sur le même ensemble de variables alors, on a une inconsistance (donc pas de solution), si l'intersection des intervalles $[α_1,β_1]$ et $[α_2,β_2]$ est vide.
$$ (Inc_1) \;\;\;\;\; [α_1,β_1] ∩ [α_2,β_2] = ∅ \;\;\;\; {\#(α_1, β_1, \{ L \}) \;\;\;\; \#(α_2, β_2, \{ L \}) } / { ⊥ } $$Et c'est bien le cas pour ce problème :
- si $\cl"red"{n > q}$ le problème n'a pas de solution et l'intersection des intervalles est vide, la règle d'inconsistance peut être appliquée et son résultat ($⊥$) indique que le problème n'a pas de solution
- par contre si $\cl"green"{n ≤ q}$, l'intersection des intervalles est non vide, la régle ne sera pas appliquée et le problème possède des solutions
Voici la traduction en minizinc de ce problème :
- %% ========================================================
- %% Auteur: Jean-Michel Richer
- %% email: jean-michel.richer@univ-angers.fr
- %% ========================================================
- %%
- %% Problème des pigeons (PigeonHole Problem) :
- %%
- %% Etant donné N pigeons et P pigeonniers, chaque
- %% pigeon pourra t-il trouver un pigeonnier, sachant
- %% qu'un pigeonnier ne peut accueillir qu'un seul pigeon.
- %%
- %% Ce problème admet des solutions si N <= P.
- %% Si N > P alors, il n'y a pas de solution.
- %%
- %% ========================================================
- include "globals.mzn";
- %% --------------------------
- %% Variables
- %% --------------------------
- int: N = 3;
- int: P = 3;
- array[1..N,1..P] of var 0..1 : holes;
- %% --------------------------
- %% Constraints
- %% --------------------------
- constraint forall(i in 1..N) (
- sum(holes[i,1..P]) = 1
- );
- constraint forall(j in 1..P) (
- sum(holes[1..N,j]) <= 1
- );
- %% --------------------------
- %% Search
- %% --------------------------
- solve satisfy;
- %% --------------------------
- %% Result
- %% --------------------------
- output [
- if j = 1 then "\n" else " " endif ++
- show(holes[i,j]) ++ " "
- | i in 1..N, j in 1..P
- ] ++ ["\n"];
include "globals.mzn";
int: N = 3;
int: P = 3;
array[1..N,1..P] of var 0..1 : holes;
constraint forall(i in 1..N) (
sum(holes[i,1..P]) = 1
);
constraint forall(j in 1..P) (
sum(holes[1..N,j]) <= 1
);
solve satisfy;
output [
if j = 1 then "\n" else " " endif ++
show(holes[i,j]) ++ " "
| i in 1..N, j in 1..P
] ++ ["\n"];On peut également le représenter sous forme entière
2.4.5. Pour conclure
Comme nous le verrons dans le chapitre suivant, la résolution du problème SAT peut se faire via des méthodes exactes qui peuvent prendre beaucoup de temps, mais l'utilisation de techniques comme la construction d'une solution et la vérification des inconsistances locales permet d'éliminer certaines branches de l'arbre de recherche.
L'utilisation de méthodes approchées ne garantit pas de trouver la consistance ou l'inconsistance d'un problème. On peut alors avoir recours à des méthodes hybrides qui se basent sur la construction d'une bonne solution (méthode gloutonne) puis répération de la solution.
Dans le cas du problème des pigeons, on peut utiliser les symétries sur la matrice des variables afin de résoudre efficacement le problème.
2.5. Bibliographie
- J.-M. Richer, Une approche de résolution de problèmes en logique des prédicats fondée sur des techniques de satisfaction de contraintes. PhD thesis, Université de Bourgogne, Dijon, 1999
- W. W. McCune, "Otter (organized techniques for theorem-proving and effective research) 2. 0 users guide" , 3, 1990
- J. A. Robinson, "A machine-oriented logic based on the resolution principle", Journal of the ACM, vol. 12, p. 23–41, Jan. 1965
- P. V. Hentenryck and Y. Deville, “The cardinality operator : A new logical connective for constraint logic programming,” in Constraint Logic Program- ming, Selected Research. WCLP 1991, Marseilles, France (F. Benhamou and A. Colmerauer, eds.), pp. 283–403, MIT Press, 1991
2.6. Exercice
Mettre au point un solveur pour le problème des pigeons. On donnera au programme les paramètres que sont le nombre de pigeons ($N$) et le nombre de pigeonniers ($P$).
On créera une classe pour créer une contrainte de cardinalité avec les paramètres $α$ et $β$ ainsi que les variables qui font partie de la contraintes.
Les variables booléennes seront stockées sous forme d'un tableau d'entiers. Une variable contiendra une des valeurs suivantes :
- 0 pour Faux
- 1 pour Vrai
- 2 si la variable n'a pas encore été affectée
L'interprétation d'une contrainte aura comme résultat l'une des valeurs suivantes :
- SATISFAITE : 1
- INSATISFAITE : 0
- NON_INTERPRETABLE : 2
On comptera le nombre de variables à Vrai :
- si une variable est Vraie, on incrémente le nombre de variables à vrai
- si une variable est Fausse, on ne fait rien
- si une variable n'est pas affectée, on retourne la valeur NON_INTERPRETABLE
- /**
- * sous-programme de résolution du problème avec backtrack
- */
- procedure resoudre(variables : tableau entiers;
- contraintes : tableau de Contraintes;
- int indice_variable)
- // si on a affecté toutes les variables, on vérifie si toutes les contraintes
- // sont satisfaites et dans ce cas il s'agit d'une solution
- si indice_variable >= taille(variables) alors
- si contraintes_satisfaites(contraintes, variables) = SATISFAITES alors
- affiche "Solution !"
- fin si
- sinon
- // sinon, on tente d'affecté la variable courante à Vrai, puis
- // si au moins une contrainte n'est pas satisfaite alors on
- // ne va pas plus loin
- variables[ indice_variable ] = 1
- si contraintes_satisfaites(contraintes, variables) != INSATISFAITES alors
- resoudre(variables, contraintes, indice_variable + 1)
- fin si
- // on essaye ensuite avec l'affectation de la variable à Faux et
- // si au moins une contrainte n'est pas satisfaite alors on
- // ne va pas plus loin
- variables[ indice_variable ] = 0
- si contraintes_satisfaites(contraintes, variables) != INSATISFAITES alors
- resoudre(variables, contraintes, indice_variable + 1)
- fin si
- // on remet la variable dans un état non affecté
- variables[ indice_variable ] = 2
- fin si
- fin procedure
- /**
- * fonction qui vérifie si les contraintes sont satisfaites
- */
- fonction contraintes_satisfaites(contraintes : tableau de Contraintes,
- variables : tableau entiers) : entier
- var valeur_retour : entier =
- pour chaque contrainte de contraintes faire
- selon que la contrainte est
- SATISFAITE: ne rien faire;
- INSATISFAITE: retourner INSATISFAITES
- NON_INTERPRETABLE: retourner NON_INTERPRETABLES
- fin si
- fin pour
- retourner SATISFAITES
- fin fonction
On définira donc trois fichiers :
- cardinality_constraint.py qui définit une contrainte de cardinalité en tant que classe et permet de vérifier si cette contrainte est satisfaite
- pigeon_hole_problem.py qui définit une classe qui stocke les variables et contraintes du problème et fournit une méthode pour la recherche de solutions
- pigeons.py qui représente le programme principal
cardinality_constraint.py
- SATISFIED = 1
- UNSATISFIED = 0
- NOT_EVALUABLE = 2
- """
- PURPOSE
- Define a cardinality constraint of the form
- #(alpha, beta, L)
- which is satisfied if at least alpha and
- at most beta literal of L are set to true
- PARAMETERS
- - alpha : minimum of literals that should be true
- - beta : maximum of literals that should be true
- - variables_index : list of the indices of variables
- """
- class CardinalityConstraint(object):
- """
- Constructor
- """
- def __init__(self, alpha, beta, variables_index):
- self.alpha = alpha
- self.beta = beta
- self.variables_index = variables_index
- """
- return
- - NOT_EVALUABLE if at least one variable
- is not assigned true (1) or false (0)
- - SATISIFIED if all variables are assigned
- a value and that the number of variables
- set to true is in [alpha,beta]
- - UNSATISIFIED if all variables are assigned
- a value and that the number of variables
- set to true is not in [alpha, beta]
- """
- def is_satisfied(self, p_variables):
- #
- # you need to implement this
- #
pigeon_hole_problem.py
- import cardinality_constraint as cc
- """
- Class used to represent the Pigeon Hole Problem
- for N pigeons and P pigeonholes
- We then have
- - N*P variables
- - N cardinality constraints of type #(1,1)
- - P cardinality constraints of type #(0,1)
- Variables are set to
- - 0 for false
- - 1 for true
- - 2 if not assigned
- """
- class PigeonHoleProblem(object):
- """
- Constructor given the number of pigeons (N)
- and the number of pigeonholes (P)
- """
- def __init__(self, N, P):
- self.N = N
- self.P = P
- self.l_variables = []
- for i in range(N*P):
- self.l_variables.append(2)
- self.l_constraints = []
- # constraint on lines (pigeons)
- for i in range(N):
- l_index = [ i*P+j for j in range(P) ]
- self.l_constraints.append( cc.CardinalityConstraint(1, 1, l_index) )
- # constraints on columns (holes)
- for j in range(P):
- l_index = [ i*P+j for i in range(N) ]
- self.l_constraints.append( cc.CardinalityConstraint(0, 1, l_index) )
- """
- Check if all constraints are satisfied and return
- - cardinality_constraint.SATISFIED
- if all constraints are satisfied
- - cardinality_constraint.UNSATISFIED
- if at least one constraint is not satisfied
- - cardinality_constraint.NOT_EVALUABLE
- if at least one constraint is not evaluable
- because if contains variables which are
- not assigned the value true (1) or false (0)
- """
- def constraints_are_satisfied(self, l_v, l_c):
- #
- # you need to implement this
- #
- """
- Print a solution as a matrix of N rows
- and P columns given a list of variables
- """
- def print_solution(self, l_v):
- #
- # you need to implement this
- #
- """
- Method that recursively solves the problem
- by trying to assign the value true (1) or false (0)
- to the current variable and then passes to the next
- variable is there is no unsatisfied constraint.
- When all variables are assigned a value then we
- check if it is a solution.
- """
- def _solve_(self, l_v, l_c, index):
- #
- # you need to implement this
- #
- """
- Main method that must be called to solve the Pigeon Hole
- Problem. This method will print the number of solutions
- found at the end.
- This method calls the _solve_ method that recursively
- looks for a solution
- """
- def solve(self):
- self.nbr_solutions = 0
- self._solve_(self.l_variables, self.l_constraints, 0)
- print("nbr_solutions=", self.nbr_solutions)
pigeons.py
- import cardinality_constraint as cc
- import pigeon_hole_problem as php
- import sys
- php = php.PigeonHoleProblem(3, 3)
- php.solve()