<< Page principale

6. Le problème du sac à dos

6.1. Définition

Le problème du sac à dos (Knapsack problem) consiste, étant donnés des articles définis par leur poids $w_i$ et leur profit $p_i$, à remplir un sac à dos de poids maximal donné en maximisant le profit.

Pour résoudre ce problème, on cherche donc les $a_i ∈ [0,1]$ tels que :

$$ \{ \table max ∑↙{i=1}↖{n} p_i × a_i ; ∑↙{i=1}↖{n} w_i × a_i ≤ w_{max} ; $$

si $a[i]=1$ alors le ième élément doit être mis dans le sac à dos.

En fait ce problème se rencontre dans différents domaines de la vie courante au niveau des entreprises et peut être étendu. On peut penser au remplissage d'un camion avec des colis : il faut maximiser l'espace occupé en respectant la contrainte sur le poids total que peut transporter le camion.

Pour en savoir plus : Interstices

Quelle est la complexité du problème ?

Elle est définie par le nombre de parties de $k$ éléments dans un ensemble de $n$ éléments, pour $k$ variant de 1 à $n$ :

$$ ∑↙{k=1}↖{n} C_n^k = 2^n - 1 $$

Exemple

Prenons l'exemple suivant avec 4 articles :

 Objet   Profit   Poids 
 O1   7   13 
 O2   4   12 
 O3   3   8 
 O4   11   3 

Si on génère toutes les combinaisons possibles, on obtient le tableau ci-après. On peut cliquer sur le titre de la colonne du tableau afin de trier les données en ordre croissant (binaire, profit ou poids) :

Binaire O4 O3 O2 O1 Profit Poids
Profits et Poids

S'il reste envisageable de réaliser ce tableau pour un petit nombre d'articles, cela devient inenvisageable dès lors que ce nombre d'articles est grand.

6.2. Résolution

Voici une instance du problème dont le format est le suivant :

10 269
55 95
10 4
47 60
5 32
4 23
50 72
8 80
61 62
85 65
87 46

Voici le code python correspondant au stockage des informations :

poids_maximum = 269

poids   = [ 95, 4, 60, 32, 23, 72, 80, 62, 65, 46]
profits = [ 55, 10, 47, 5, 4, 50, 8, 61, 85, 87 ]

6.2.1. Méthode approchée

Exercice 6.1

Pour ce problème le profit maximum que l'on peut atteindre est de 295 pour un poids égal au poids maximum. Ecrire un programme simple qui permet d'obtenir ce résultat.

On utilise la méthode approchée suivante :

  • calculer les $p_i / w_i$ et trier les objets en ordre décroissant de cette quantité
  • mettre les objets dans le sac dans l'ordre indiqué et retirer le dernier objet s'il dépasse le poids maximum qui est de 269.

sad_heuristique.py

  1. # ###################################################################
  2. #
  3. #       Program: sad_heuristique.py
  4. #        Author: Jean-Michel Richer
  5. #  Organisation: Computer Science Department,
  6. #                University of Angers,
  7. #                France
  8. #         Email: jean-michel.richer@univ-angers.fr
  9. # Creation date: April, 2021
  10. #  Modification: April, 2021
  11. #
  12. # ###################################################################
  13. #
  14. # Aim:
  15. #
  16. #    This program is an implementation of a heuristic method used
  17. #    to find a solution to the knapsack problem. The method is
  18. #    derived from https://interstices.info/le-probleme-du-sac-a-dos/
  19. #    and uses the ratio profit / weight of each object
  20. #
  21. # Objectif :
  22. #
  23. #    Ce programme repose sur l'utilisation d'une heuristique afin
  24. #    de résoudre le problème du sac à dos. La méthode est issue
  25. #    du site https://interstices.info/le-probleme-du-sac-a-dos/
  26. #    et repose sur l'utilisation du ratio profit / poids des objets
  27. #
  28. # ###################################################################
  29. #
  30. # License
  31. #
  32. #    This program is a free software you can modifiy it and
  33. #    redistribute it for non profitable use.
  34. #
  35. # ###################################################################
  36.  
  37.  
  38. import random
  39. import sys
  40.  
  41. #
  42. # Données du problème
  43. # Poids maximum autorisé et données de poids et profit
  44. #
  45.  
  46. poids_maximum = 269
  47. poids   = [ 95, 4, 60, 32, 23, 72, 80, 62, 65, 46]
  48. profits = [ 55, 10, 47, 5, 4, 50, 8, 61, 85, 87 ]
  49.  
  50. # ===================================================================
  51. # Classe qui permet de représenter les objets à mettre dans le sac
  52. # à dos. Un objet possède un poids, un profit et un ratio égal au
  53. # rapport profit / poids
  54. # ===================================================================
  55. class Objet(object):
  56.  
  57.     """
  58.     class used to represent an object
  59.        
  60.     Attributes
  61.     ----------
  62.     poids : int
  63.       weight of the object
  64.     profit : int
  65.       profit of the object
  66.     ratio : float
  67.       ratio profit / poids
  68.      
  69.     Methods
  70.     -------
  71.      __str__()
  72.        transform the object into a string
  73.     """
  74.    
  75.     def __init__(self, id, poids, profit):
  76.         """
  77.         Constructor
  78.        
  79.         Parameters
  80.         ----------
  81.         id : int
  82.           object identifier from 1 to N
  83.         poids : int
  84.           weight of the object
  85.         profit : int
  86.           profit de l'objet
  87.            
  88.         """
  89.         self.id = id
  90.         self.profit = profit
  91.         self.poids = poids
  92.         self.ratio = profit / poids
  93.    
  94.     def __str__(self):
  95.         """
  96.         Transform the object into a string    
  97.         """    
  98.         return "(" + str(self.id) + ",p=" + str(self.poids) + ",w=" + str(self.profit) + ",r={0:.2f}".format(self.ratio) + ")"
  99.        
  100.  
  101. # ===================================================================
  102. # Classe qui permet de représenter un sac à dos composé d'une liste
  103. # de présence/absence d'objets, du poids et profit total qui
  104. # résulte de la présence/absence des objets
  105. # ===================================================================
  106. class Sac(object):
  107.     """
  108.     Knapsack representation as a list of present/absent objects,
  109.     the weight and the profit
  110.    
  111.     Attributes
  112.     ----------
  113.     objets : list
  114.         list of objects that can be put inside the knapsack
  115.     liste : list
  116.         list of 0 and 1, 1 means the object is present
  117.     poids : int
  118.         weight of the knapsack
  119.     profit : int
  120.         profit of the knapsack
  121.    
  122.    
  123.     """
  124.    
  125.     # -----------------------------------------------------
  126.     # Constructeur avec liste d'objets et liste
  127.     # présence / absence des objets
  128.     # -----------------------------------------------------
  129.     def __init__(self, objets, liste):
  130.         """
  131.         Constructor
  132.        
  133.         Parameters
  134.         ----------
  135.         objets : list of Objet
  136.           list of all possible objects that can be put
  137.           in the knapsack
  138.         liste : list of 0/1
  139.           list of objects that compose the knapsack
  140.          
  141.         """
  142.         self.objets = objets
  143.         self.liste = liste
  144.         self.poids = 0
  145.         self.profit = 0
  146.        
  147.         for i in range(len(liste)):
  148.             if liste[ i ] == 1:
  149.                 self.poids += objets[ i ].poids
  150.                 self.profit += objets[ i ].profit
  151.    
  152.         self.verbose = True
  153.        
  154.     # -----------------------------------------------------
  155.     # ajouter un objet dans le sac à dos
  156.     # -----------------------------------------------------
  157.     def ajoute_objet(self, n):
  158.         """
  159.         Add object to knapsack
  160.         """
  161.         if self.liste[ n ] == 1:
  162.             return
  163.         self.poids += self.objets[ n ].poids
  164.         self.profit += self.objets[ n ].profit
  165.         self.liste[ n ] = 1
  166.    
  167.     # -----------------------------------------------------
  168.     # retirer un objet du sac à dos
  169.     # -----------------------------------------------------            
  170.     def supprime_objet(self, n):
  171.         """
  172.         Delete object from knapsack
  173.         """
  174.         if self.liste[ n ] == 0:
  175.             return
  176.         self.poids -= self.objets[ n ].poids
  177.         self.profit -= self.objets[ n ].profit
  178.         self.liste[ n ] = 0
  179.    
  180.     # -----------------------------------------------------
  181.     # Convertion un sac à dos en chaine
  182.     # -----------------------------------------------------            
  183.     def __str__(self):
  184.         """
  185.         Transform object into string
  186.         """
  187.         return "(poids=" + str(self.poids) + ",profit=" + str(self.profit) + "," + str(self.liste) + ")"
  188.  
  189.     # -----------------------------------------------------
  190.     # Copie d'un sac à dos
  191.     # -----------------------------------------------------
  192.     def copy(self):
  193.         """
  194.         Create copy of the object
  195.         """
  196.         sac = Sac(self.objets, self.liste.copy())
  197.         sac.poids = self.poids
  198.         sac.profit = self.profit
  199.         return sac
  200.  
  201.  
  202.  
  203.  
  204. # ===================================================================
  205. # Classe représentant un solveur de type heuristique
  206. # ===================================================================
  207. class SAD(object):
  208.     """
  209.     This class is a solver based on a heuristic
  210.     """
  211.    
  212.     # -----------------------------------------------------
  213.     # Constructeur
  214.     # -----------------------------------------------------
  215.     def __init__(self, poids_maximum, poids, profits):
  216.         """
  217.         Constructor given maximum weight of knapsack, weights and
  218.         profits of objects that can be put in the knaspsack.
  219.         Objects are created in this class and are provided to the
  220.         Sac class
  221.         """
  222.         self.poids_maximum = poids_maximum
  223.         self.profits = profits
  224.         self.poids = poids
  225.  
  226.         self.nbr_objets = len(poids)
  227.         self.objets = [ ]
  228.        
  229.         for i in range(len(poids)):
  230.             objet = Objet(i+1, poids[i], profits[i])
  231.             self.objets.append( objet )
  232.  
  233.         self.verbose = True
  234.        
  235.     # -----------------------------------------------------
  236.     # Méthode heuristique basée sur le ratio profit / poids
  237.     # -----------------------------------------------------
  238.     def methode_heuristique(self):
  239.         """
  240.         Heuristic-based method with the ratio profit / weight.
  241.         Objects are ordered followinf this ratio and added
  242.         to the knaspsack if they don't exceed the maximum
  243.         weight
  244.         """
  245.         print("=" * 40)
  246.         print(" Début de la méthode heuristique ")
  247.         print("=" * 40)
  248.        
  249.         # tri suivant le ratio, les objets les plus
  250.         # intéressant sont en début de liste
  251.         @@@...@@@
  252.        
  253.        
  254.         print("-" * 30)
  255.         print(" Objets triés suivant ratio  décroissant")
  256.         print("-" * 30)
  257.         for obj in self.objets:
  258.             print(obj)
  259.  
  260.        
  261.         # indice de l'objet
  262.         i = 0
  263.         # sac vide
  264.         sac = Sac(self.objets, [0 for x in self.objets ])
  265.        
  266.         # pour chaque objet
  267.         while i < len(self.objets):
  268.             # si le poids maximum n'est pas dépassé
  269.             # ajouter l'objet dans le sac
  270.             @@@...@@@
  271.            
  272.             i += 1
  273.  
  274.         print("-" * 30)
  275.         print(" Objetf inal      ")
  276.         print("-" * 30)
  277.         print( str( sac ) )
  278.  
  279.         return sac
  280.    
  281.     # -----------------------------------------------------
  282.     # Affiche le résultat
  283.     # -----------------------------------------------------
  284.     def print(self, sac):
  285.         print("-" * 30)
  286.         print(" Contenu du sac ")
  287.         print("-" * 30)
  288.  
  289.         for i in range(len(self.objets)):
  290.             if sac.liste[i] == 1:
  291.                 print(self.objets[i])
  292.         print("profit_total=" + str(sac.profit), end=',')
  293.         print("poids_total=" + str(sac.poids))
  294.  
  295.     # -----------------------------------------------------
  296.     # Amélioration : suppression d'un élément puis tentative
  297.     # d'en ajouter un autre
  298.     # -----------------------------------------------------
  299.     def ameliore(self, sac):
  300.         """
  301.         Improvement of the knapsack : we remove each object
  302.         in the knapsack and try to add other objects not
  303.         present.
  304.         """
  305.         print()
  306.         print("=" * 40)
  307.         print(" Méthode avec amélioration ")
  308.         print("=" * 40)
  309.        
  310.         sacs_ameliores = []
  311.        
  312.         print(sac.liste)
  313.         # pour chaque objet
  314.         for k in range(len(sac.liste)):
  315.  
  316.             # supprimer le k-ieme objet
  317.             if sac.liste[ k ] == 0:
  318.                 continue
  319.            
  320.             # créer une copie du sac sans l'objet qui doit être supprimé
  321.             sac_allege = sac.copy()
  322.             sac_allege.supprime_objet(k)
  323.            
  324.             # calcul du poids et profit du sac allege
  325.            
  326.             if self.verbose:
  327.                 print("-" * 30)
  328.                 print(" Sac avec objet supprimé ")
  329.                 print("-" * 30)
  330.                
  331.                 print("- on supprime ", self.objets[ k ])
  332.                 print("-" * 40 )
  333.                    
  334.                 print("- poids  allege=", sac_allege.poids)    
  335.                 print("- profit allege=", sac_allege.profit)  
  336.  
  337.             # on tente d'ajouter un nouvel objet s'il n'est pas
  338.             # déjà dans la liste des objets
  339.             @@@...@@@
  340.                        
  341.             sacs_ameliores.append( sac_allege )        
  342.                
  343.          
  344.         return sacs_ameliores
  345.    
  346. # ===================================================================
  347. # Programme principal
  348. # ===================================================================
  349.  
  350. HELP_MESSAGE = """
  351. Program arguments are:
  352.  
  353. -h or --help
  354.     to get this message
  355.  
  356. -q or --quiet
  357.     to remove verbose mode and avoid to display graphics
  358.    
  359. """
  360.  
  361. sad = SAD(poids_maximum, poids, profits)
  362.  
  363. # gestion des arguments du programme
  364. if len(sys.argv) >= 1:
  365.     try:
  366.         for i in range(1, len(sys.argv)):
  367.             arg = sys.argv[i]
  368.             if arg == "-h" or arg == "--help":
  369.                 print( HELP_MESSAGE )
  370.  
  371.             elif arg == "-q" or arg == "--quiet":
  372.                 sad.verbose = False            
  373.  
  374.             else:
  375.                 raise ValueError("Unexpected argument")
  376.                
  377.     except:
  378.         print("="*40)
  379.         print(sys.exc_info()[1])
  380.         print("="*40)
  381.         print( HELP_MESSAGE )
  382.         sys.exit(1)
  383.  
  384.  
  385. print()
  386. print("*" * 40)
  387. print("Heuristique pour créer un sac")
  388. print("*" * 40)
  389.  
  390.  
  391. sac = sad.methode_heuristique()
  392.  
  393. print()
  394. print("*" * 40)
  395. print(" Amélioration")
  396. print("*" * 40)
  397.  
  398. sac_ameliores = sad.ameliore(sac)
  399.  
  400. print()
  401. for sac in sac_ameliores:
  402.     sad.print( sac )
  403.  
  404. print()
  405. sac_ameliores.sort(key= lambda x : x.poids)
  406. for sac in sac_ameliores:
  407.     print("- " + str(sac) )
  408.  
  409.  
  410.  

On devrait obtenir le résultat suivant :

======================
Objets triés
======================
(2,p=10,w=4,r=2.50)
(10,p=87,w=46,r=1.89)
(9,p=85,w=65,r=1.31)
(8,p=61,w=62,r=0.98)
(3,p=47,w=60,r=0.78)
(6,p=50,w=72,r=0.69)
(1,p=55,w=95,r=0.58)
(5,p=4,w=23,r=0.17)
(4,p=5,w=32,r=0.16)
(7,p=8,w=80,r=0.10)
======================
Recherche heuristique
======================
ajoute (2,p=10,w=4,r=2.50), poids=4
ajoute (10,p=87,w=46,r=1.89), poids=50
ajoute (9,p=85,w=65,r=1.31), poids=115
ajoute (8,p=61,w=62,r=0.98), poids=177
ajoute (3,p=47,w=60,r=0.78), poids=237
ajoute (5,p=4,w=23,r=0.17), poids=260

===== SAC ======
(2,p=10,w=4,r=2.50)
(10,p=87,w=46,r=1.89)
(9,p=85,w=65,r=1.31)
(8,p=61,w=62,r=0.98)
(3,p=47,w=60,r=0.78)
(5,p=4,w=23,r=0.17)
profit_total=294
poids_total=260

La meilleure solution trouvée avec la méthode heuristique est de profit 294 et de poids total 260, or l'optimum global possède un profit de 295 et un poids total de 269.

6.2.2. Algorithme génétique

Exercice 6.2

Ecrire un algorithme génétique qui permet de résoudre le problème du sac à dos. On utilisera une population de 30 individus qui seront générés aléatoirement ainsi que 50 générations.

A chaque génération, on choisit aléatoirement deux individus (père et mère) et on choisit également de manière aléatoire le point où on coupe les solutions afin de générer deux enfants :

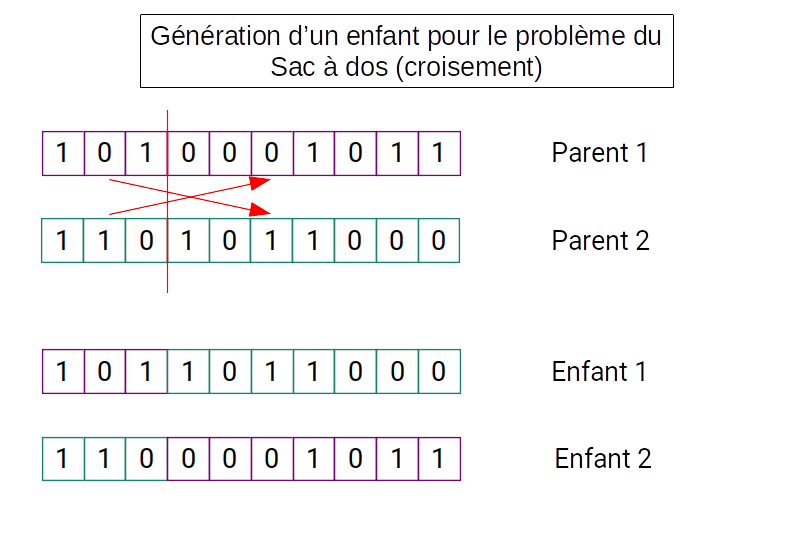
  • on génére deux enfants par croisement (crossover)
  • on applique une mutation sur chaque enfant
  • on garde le meilleur des deux enfants
  • on remplace le père ou la mère si l'enfant est meilleur que son père ou sa mère

L'opération de mutation consiste à :

  • ajouter des objets si le poids maximal n'est pas atteint (sans le dépasser)
  • ou à retirer des objets si on dépasse le poids maximal.

sad_algorithme_genetique.py

  1. # ###################################################################
  2. #
  3. #       Program: sad_algorithme_genetique.py
  4. #        Author: Jean-Michel Richer
  5. #  Organisation: Computer Science Department,
  6. #                University of Angers,
  7. #                France
  8. #         Email: jean-michel.richer@univ-angers.fr
  9. # Creation date: April, 2021
  10. #  Modification: April, 2021
  11. #
  12. # ###################################################################
  13. #
  14. # Aim:
  15. #
  16. #    This program is an implementation of a genetic algorithm used
  17. #    to find a solution to the knapsack problem. The method is based
  18. #    on a population that evolves using a crossover operator,
  19. #    mutations on children and replacement of parents if the best
  20. #    child is better than is father or mother.
  21. #
  22. # Objectif :
  23. #
  24. #    Ce programme repose sur l'utilisation d'un algorithme
  25. #    génétique afin de résoudre le problème du sac à dos. La méthode
  26. #    repose sur l'évolution d'une population grâce à un opérateur
  27. #    de croisement, la mutation des enfants et le remplacement
  28. #    de l'un des parent si un des enfants est meilleur que ses
  29. #    parents.
  30. #
  31. # ###################################################################
  32. #
  33. # License
  34. #
  35. #    This program is a free software you can modifiy it and
  36. #    redistribute it for non profitable use.
  37. #
  38. # ###################################################################
  39.  
  40. import random
  41. import sys
  42. import matplotlib.pyplot as plt
  43. import numpy as np
  44. import statistics as stats
  45.  
  46. """
  47.    Les données de ce problème sont issues du site suivant :
  48.    
  49.    https://interstices.info/le-probleme-du-sac-a-dos/
  50.    
  51.    La méthode de résolution utilisée est une méthode approchée
  52.    qui se fonde sur l'utilisation des ratios p_i/w_i de
  53.    chaque objet. Les objets sont triés suivant un ordre
  54.    décroissant de ces ratios.
  55. """
  56. #
  57. # Données du problème
  58. # Poids maximum autorisé et données de poids et profit
  59. #
  60. poids_maximum = 269
  61. poids   = [ 95, 4, 60, 32, 23, 72, 80, 62, 65, 46]
  62. profits = [ 55, 10, 47, 5, 4, 50, 8, 61, 85, 87 ]
  63.  
  64. # ===================================================================
  65. # Classe qui permet de représenter les objets à mettre dans le sac
  66. # à dos. Un objet possède un poids, un profit
  67. # ===================================================================
  68. class Objet(object):
  69.  
  70.     """
  71.     class used to represent an object
  72.        
  73.     Attributes
  74.     ----------
  75.     poids : int
  76.       weight of the object
  77.     profit : int
  78.       profit of the object
  79.      
  80.     Methods
  81.     -------
  82.      __str__()
  83.        transform the object into a string
  84.     """
  85.    
  86.     def __init__(self, id, poids, profit):
  87.         """
  88.         Constructor
  89.        
  90.         Parameters
  91.         ----------
  92.         id : int
  93.           object identifier from 1 to N
  94.         poids : int
  95.           weight of the object
  96.         profit : int
  97.           profit de l'objet
  98.            
  99.         """
  100.         self.id = id
  101.         self.profit = profit
  102.         self.poids = poids
  103.    
  104.     def __str__(self):
  105.         """
  106.         Transform object into string    
  107.         """    
  108.         return "(" + str(self.id) + ",p=" + str(self.poids) + ",w=" + str(self.profit) + ",r={0:.2f}".format(self.ratio) + ")"
  109.  
  110.  
  111. # ===================================================================
  112. # Classe qui permet de représenter un sac à dos composé d'une liste
  113. # de présence/absence d'objets, du poids et profit total qui
  114. # résulte de la présence/absence des objets
  115. # ===================================================================
  116. class Sac(object):
  117.     """
  118.     Knapsack representation as a list of present/absent objects,
  119.     the weight and the profit
  120.    
  121.     Attributes
  122.     ----------
  123.     objets : list
  124.         list of objects that can be put inside the knapsack
  125.     liste : list
  126.         list of 0 and 1, 1 means the object is present
  127.     poids : int
  128.         weight of the knapsack
  129.     profit : int
  130.         profit of the knapsack
  131.    
  132.    
  133.     """
  134.    
  135.     # -----------------------------------------------------
  136.     # Constructeur avec liste d'objets et liste
  137.     # présence / absence des objets
  138.     # -----------------------------------------------------
  139.     def __init__(self, objets, liste):
  140.         """
  141.         Constructor
  142.         """
  143.         self.objets = objets
  144.         self.liste = liste
  145.         self.poids = 0
  146.         self.profit = 0
  147.        
  148.         for i in range(len(liste)):
  149.             if liste[ i ] == 1:
  150.                 self.poids += objets[ i ].poids
  151.                 self.profit += objets[ i ].profit
  152.  
  153.     # -----------------------------------------------------
  154.     # ajouter un objet dans le sac à dos
  155.     # -----------------------------------------------------
  156.     def ajoute_objet(self, n):
  157.         """
  158.         Add object to knapsack
  159.         """
  160.         if self.liste[ n ] == 1:
  161.             return
  162.         self.poids += self.objets[ n ].poids
  163.         self.profit += self.objets[ n ].profit
  164.         self.liste[ n ] = 1
  165.  
  166.     # -----------------------------------------------------
  167.     # retirer un objet du sac à dos
  168.     # -----------------------------------------------------                        
  169.     def supprime_objet(self, n):
  170.         """
  171.         Delete object from knapsack
  172.         """
  173.         if self.liste[ n ] == 0:
  174.             return
  175.         self.poids -= self.objets[ n ].poids
  176.         self.profit -= self.objets[ n ].profit
  177.         self.liste[ n ] = 0
  178.  
  179.     # -----------------------------------------------------
  180.     # Convertion un sac à dos en chaine
  181.     # -----------------------------------------------------                
  182.     def __str__(self):
  183.         """
  184.         Transform object into string
  185.         """
  186.         return "(poids=" + str(self.poids) + ",profit=" + str(self.profit) + "," + str(self.liste) + ")"
  187.  
  188.     # -----------------------------------------------------
  189.     # Copie d'un sac à dos
  190.     # -----------------------------------------------------
  191.     def copy(self):
  192.         """
  193.         Create copy of the object
  194.         """
  195.         sac = Sac(self.objets, self.liste.copy())
  196.         sac.poids = self.poids
  197.         sac.profit = self.profit
  198.         return sac
  199.  
  200.     # -----------------------------------------------------
  201.     # Mutation d'un objet
  202.     # -----------------------------------------------------
  203.     def mutation(self, poids_maximum):
  204.         """
  205.         Mutation of the knapsac which consists in removing objects
  206.         if the weight of the knapsack is greater than the maximum
  207.         weight or to add objects if the weight of the knapsack
  208.         is smaller than the maximum weight
  209.        
  210.         Parameters
  211.         ----------
  212.         poids_maximum : int
  213.           maximum weight allowed
  214.          
  215.         """
  216.         if self.poids == poids_maximum:
  217.             return
  218.        
  219.         # on définit un ordre aléatoire de prise en compte
  220.         # des objets
  221.         ordre = [ x for x in range(len(self.liste)) ]
  222.         random.shuffle(ordre)
  223.  
  224.         # si le poids de l'objet est supérieur au poids maximum
  225.         if self.poids > poids_maximum:
  226.        
  227.             # on supprime des objets en suivant l'ordre
  228.             @@@...@@@
  229.            
  230.         # si le poids de l'objet est inférieur au poids maximum
  231.         else:
  232.        
  233.             # on ajoute des objets en suivant l'ordre
  234.             @@@...@@@
  235.    
  236.     # -----------------------------------------------------
  237.     #   Fonction qui indique si un objet est meilleur qu'un autre.
  238.     #   L'objet courant est meilleur qu'un autre objet si lorsque
  239.     #   son profit est supérieur à celui de l'autre objet, sa
  240.     #   distance au poids maximum est inférieure à celle de l'autre
  241.     #   objet
  242.     # -----------------------------------------------------
  243.     def est_meilleur(self, autre, poids_maximum):
  244.         """
  245.         Comparison of two knapsacks based on profit and weight
  246.    
  247.         Parameters
  248.         ----------
  249.         autre : Sac
  250.           other knapsack for comparison
  251.         poids_maximum : int
  252.           maximum weight allowed   
  253.         """    
  254.         @@@...@@@
  255.  
  256.  
  257. # ===================================================================
  258. # Classe représentant un solveur de type algorithme génétique
  259. # ===================================================================
  260. class SAD(object):
  261.     """
  262.     This class is a solver based on a Genetic Algorithm
  263.     """
  264.    
  265.     def __init__(self, poids_maximum, poids, profits):
  266.         """
  267.         Constructor given maximum weight of knapsack, weights and
  268.         profits of objects that can be put in the knaspsack.
  269.         Objects are created in this class and are provided to the
  270.         Sac class
  271.         """
  272.        
  273.         self.poids_maximum = poids_maximum
  274.         self.profits = profits
  275.         self.poids = poids
  276.         self.nbr_objets = len(poids)
  277.  
  278.         #
  279.         # création des objets
  280.         #
  281.         self.objets = []
  282.        
  283.         for i in range(len(profits)):
  284.             objet = Objet(i, poids[i], profits[i])
  285.             self.objets.append( objet )
  286.  
  287.         self.verbose = False
  288.        
  289.         # données stockées concernant l'évolution
  290.         # de la population afin d'afficher des
  291.         # graphiques
  292.         self.copie_population_initiale = []
  293.         self.liste_evolution_score_minimum = []
  294.         self.liste_evolution_score_maximum = []
  295.         self.liste_evolution_score_moyen   = []
  296.  
  297.            
  298.     # -----------------------------------------------------
  299.     # croisement entre deux individus
  300.     # -----------------------------------------------------
  301.     def croisement(self, pere, mere):
  302.         """
  303.         Crossover operation given two parents. The list of
  304.         present/absent objects is considered as a chromosome
  305.         and is cut at a certain point
  306.        
  307.         Parameters
  308.         ----------
  309.         pere : Sac
  310.             father
  311.         mere : Sac
  312.             mother
  313.         """  
  314.        
  315.         # enfants générés
  316.         enfant1 = None
  317.         enfant2 = None
  318.  
  319.         # point de coupure du chromosome
  320.         point_de_coupure = @@@...@@@
  321.        
  322.         l_enfant1 = @@@...@@@
  323.         l_enfant2 = @@@...@@@
  324.        
  325.         enfant1 = Sac( self.objets, l_enfant1 )
  326.         enfant2 = Sac( self.objets, l_enfant2 )
  327.  
  328.         if self.verbose:
  329.             print("cut=",point_de_coupure)
  330.             print(pere)
  331.             print(mere)
  332.             print(enfant1)
  333.             print(enfant2)
  334.  
  335.         return enfant1, enfant2
  336.  
  337.     # -----------------------------------------------------
  338.     # Modification de la population en fonction du fait
  339.     # que les enfants sont meilleurs que le père et la
  340.     # mère
  341.     # -----------------------------------------------------
  342.     def remplacement(self, pere, mere, enfant1, enfant2):  
  343.         """
  344.         Modification of the population : we keep the best child which replaces
  345.         the mother or the father if he is better than one of them
  346.         """
  347.        
  348.         if self.verbose:
  349.             print( "enfant1 muté : ", enfant1 )
  350.             print( "enfant2 muté : ", enfant2 )
  351.            
  352.         # choisir le meilleur enfant
  353.         if enfant1.est_meilleur( enfant2, self.poids_maximum ):
  354.             enfant = enfant1
  355.         else:
  356.             enfant = enfant2
  357.        
  358.         # remplacer le pere
  359.         remplacement = False
  360.         if enfant.est_meilleur(pere, self.poids_maximum):
  361.             self.population.remove( pere )
  362.             self.population.append( enfant )
  363.             remplacement = True
  364.        
  365.         if enfant.est_meilleur(mere, self.poids_maximum) and remplacement == False:
  366.             self.population.remove( mere )
  367.             self.population.append( enfant )
  368.  
  369.     # -----------------------------------------------------
  370.     # Enregistre les données pour créer les graphiques
  371.     # -----------------------------------------------------
  372.     def enregistre_donnees(self):
  373.         """
  374.         Record data to display graphics
  375.         """
  376.         # enregistre les données de l'évolution de la population
  377.         minimum = min(self.population, key=lambda x: x.profit)
  378.         maximum = max(self.population, key=lambda x: x.profit)
  379.         somme = 0
  380.         for individu in self.population:
  381.             somme += individu.profit
  382.         moyenne = somme / len(self.population)
  383.            
  384.         self.liste_evolution_score_minimum.append( minimum.profit )
  385.         self.liste_evolution_score_maximum.append( maximum.profit )
  386.         self.liste_evolution_score_moyen.append( moyenne )
  387.            
  388.                    
  389.     # -----------------------------------------------------
  390.     # Méthode de résolution basée sur un algorithme
  391.     # génétique
  392.     # -----------------------------------------------------
  393.     def algorithme_genetique(self, taille_population, nombre_de_generations):
  394.         """
  395.        Genetic algorithm to solve the problem.
  396.        
  397.        Parameters
  398.        ----------
  399.        taille_population : int
  400.             population size
  401.        nombre_de_generations : int
  402.             maximum number of generations
  403.         """
  404.        
  405.         self.nombre_de_generations = nombre_de_generations
  406.  
  407.         #
  408.         # Générer la population initiale de manière aléatoire
  409.         #
  410.         self.population = [ ]
  411.         for i in range(taille_population):
  412.             objets_selectionnes = []
  413.            
  414.             while len(objets_selectionnes) != len(self.objets):
  415.                 x = random.randint(0, 1)
  416.                 objets_selectionnes.append(x)
  417.                
  418.             self.population.append( Sac( self.objets, objets_selectionnes ) )
  419.  
  420.         # enregistrement de la population initiale pour affichage graphique
  421.         self.population_initiale = self.population.copy()
  422.  
  423.         self.enregistre_donnees()
  424.        
  425.         #
  426.         # Trier la population suivant le poids
  427.         #
  428.        
  429.         @@@...@@@
  430.  
  431.         #
  432.         # Algorithme génétique
  433.         #
  434.        
  435.         generation = 1
  436.        
  437.         while generation <= nombre_de_generations:
  438.            
  439.             print("==== GENERATION ", generation, "====")
  440.            
  441.             # choix aléatoire de deux parents        
  442.             p = @@@...@@@
  443.             m = @@@...@@@
  444.             @@@...@@@
  445.            
  446.             if self.verbose:
  447.                 print("pere indice =", p)
  448.                 print("mere indice =", m)
  449.                
  450.             pere = self.population[ p ]
  451.             mere = self.population[ m ]
  452.            
  453.             # génération des enfant par croisement
  454.            
  455.             enfant1, enfant2 = self.croisement( pere, mere )
  456.  
  457.             if self.verbose:
  458.                 print("===========================")
  459.                 print("pere    : ", pere)
  460.                 print("mere    : ", mere)
  461.                 print("enfant1 : ", enfant1)
  462.                 print("enfant2 : ", enfant2)
  463.            
  464.             # mutation des enfants
  465.            
  466.             enfant1.mutation( self.poids_maximum )
  467.             enfant2.mutation( self.poids_maximum )
  468.            
  469.             # remplacement de la population
  470.            
  471.             self.remplacement(pere, mere, enfant1, enfant2)
  472.                        
  473.             self.enregistre_donnees()
  474.                                    
  475.             generation += 1
  476.            
  477.            
  478.         # tri des sac finaux suivant le poids 
  479.            
  480.         self.population.sort(key=lambda x : x.poids)
  481.  
  482.         self.population_finale = self.population.copy()
  483.        
  484.         candidats = [ individu for individu in self.population if individu.poids <= self.poids_maximum ]
  485.  
  486.         return candidats
  487.  
  488.     # -----------------------------------------------------
  489.     # Affiche deux graphiques
  490.     # - le premier concerne l'évolution des scores (profit)
  491.     #   minimum, moyen et maximum de la populationen en
  492.     #   fonction du nombre de génération
  493.     # - second affiche les populations initiales et finales
  494.     #   en fonction du poids et du profit ainsi que les
  495.     #   solutions potentielles de la population finale
  496.     # -----------------------------------------------------
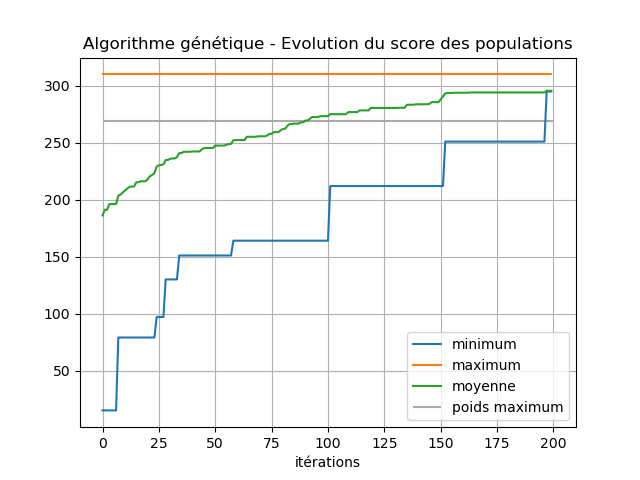
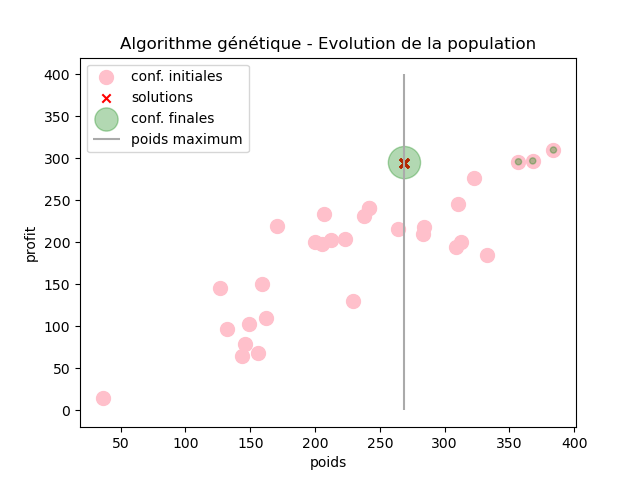
  497.     def graphique(self):
  498.         """
  499.         Display two graphics:
  500.         - the first one is the evolution of the profit of the
  501.           population, we show the minimum, average and maximum
  502.           values over the generations
  503.         - the second one displays the initial and final
  504.           populations in function of the weight and profit
  505.           as well as the possible solutions
  506.         """
  507.         # une génération en plus la première, génération 0
  508.         x = range( self.nombre_de_generations + 1)
  509.        
  510.         plt.grid()
  511.         plt.plot( x, self.liste_evolution_score_minimum, label='minimum' )
  512.         plt.plot( x, self.liste_evolution_score_maximum, label='maximum' )
  513.         plt.plot( x, self.liste_evolution_score_moyen, label='moyenne' )
  514.         plt.hlines( self.poids_maximum, 0, self.nombre_de_generations, color='#aaa',label="poids maximum")
  515.         plt.xlabel('itérations')
  516.         plt.legend()
  517.         plt.title('Algorithme génétique - Evolution du score des populations')
  518.         plt.show()
  519.  
  520.         initial_poids    = [individu.poids  for individu in self.population_initiale]
  521.         initial_profits  = [individu.profit for individu in self.population_initiale]
  522.         final_poids      = [individu.poids  for individu in self.population_finale]
  523.         final_profits    = [individu.profit for individu in self.population_finale]
  524.         possible_poids   = [individu.poids  for individu in self.population_finale if individu.poids <= self.poids_maximum]
  525.         possible_profits = [individu.profit for individu in self.population_finale if individu.poids <= self.poids_maximum]
  526.  
  527.         fig, ax = plt.subplots()
  528.         plt.scatter(initial_poids, initial_profits, s=100.0, color='#A0A0A0', label='conf. initiales')
  529.        
  530.         unique_confs = {}
  531.         for individu in self.population:
  532.             poids_profit = str( individu.poids ) + ',' + str( individu.profit )
  533.             if unique_confs.get( poids_profit ) == None:
  534.                 unique_confs[ poids_profit ] = 1
  535.             else:
  536.                 unique_confs[ poids_profit ] += 1
  537.  
  538.         print("-------------------------------------")
  539.         print("   Nombre d'occurrences de chaque    ")
  540.         print("configuration de la population finale")
  541.         print("     (diversité de la population)    ")
  542.         print("-------------------------------------")
  543.         print("poids maximum = ", self.poids_maximum)
  544.         print("-------------------------------------")
  545.         print(" poids,profit : occurrences")
  546.         print("-------------------------------------")
  547.         for poids_profit, n_occ in unique_confs.items():
  548.             poids, profit = poids_profit.split(',')
  549.             poids = int(poids)
  550.             if poids <= self.poids_maximum:
  551.                 solution = " solution "
  552.             else:
  553.                 solution = "   "
  554.             print( "{0:7s} : {1:3d} {2:s}".format( poids_profit, n_occ, solution ) )
  555.  
  556.         print("-------------------------------------")
  557.         print("Note : les solutions sont les configurations")
  558.         print("de la population finale en dessous de la    ")
  559.         print("limite de poids autorisée")
  560.  
  561.         x = []
  562.         y = []
  563.         z = []
  564.  
  565.         for v in unique_confs:
  566.             poids, profit = v.split(',')
  567.             xc = int(poids)
  568.             yc = int(profit)
  569.             zc = unique_confs.get( v ) * 20
  570.             x.append( xc )
  571.             y.append( yc )
  572.             z.append( zc )
  573.  
  574.            
  575.         plt.scatter(x, y, s=z, c='#CC6900', alpha=1.0, label='conf. finales')
  576.         plt.scatter(possible_poids, possible_profits, color='#007CFF', marker='x',label='solutions')
  577.        
  578.         plt.xlabel("poids")
  579.         plt.ylabel("profit")
  580.         plt.vlines(self.poids_maximum,0,400,color='#aaa',label="poids maximum")
  581.         plt.title('Algorithme génétique - Evolution de la population')
  582.         ax.legend(loc=2)
  583.         plt.show()  
  584.        
  585.        
  586.    
  587. # ===================================================================
  588. # Programme principal
  589. # ===================================================================
  590.  
  591. HELP_MESSAGE = """
  592. Program arguments are:
  593.  
  594. -h or --help
  595.     to get this message
  596.  
  597. -q or --quiet
  598.     to remove verbose mode and avoid to display graphics
  599.    
  600. """
  601.  
  602. sad = SAD(poids_maximum, poids, profits)
  603.  
  604. taille_population = 30
  605. nombre_de_generations = 200
  606.  
  607. # gestion des arguments du programme
  608. if len(sys.argv) >= 1:
  609.     try:
  610.         i = 1
  611.         while i < len(sys.argv):
  612.             arg = sys.argv[i]
  613.             if arg == "-h" or arg == "--help":
  614.                 print( HELP_MESSAGE )
  615.  
  616.             elif arg == "-q" or arg == "--quiet":
  617.                 sad.verbose = False            
  618.  
  619.             elif arg == "-p":
  620.                 i += 1
  621.                 taille_population = int(sys.argv[i])
  622.             elif arg.startswith("--population="):
  623.                 taille_population = int(arg.split('=')[1])
  624.                
  625.             elif arg == "-g":
  626.                 i += 1
  627.                 nombre_de_generations = int(sys.argv[i])
  628.             elif arg.startswith("--generations="):
  629.                 nombre_de_generations = int(arg.split('=')[1])
  630.                
  631.                
  632.             else:
  633.                 raise ValueError("Unexpected argument")
  634.                
  635.             i += 1 
  636.                
  637.     except:
  638.         print("="*40)
  639.         print(sys.exc_info()[1])
  640.         print("="*40)
  641.         print( HELP_MESSAGE )
  642.         sys.exit(1)
  643.  
  644.  
  645. population = sad.algorithme_genetique(taille_population,
  646.     nombre_de_generations)
  647.    
  648. for individu in population:
  649.     print(individu)
  650.  
  651. sad.graphique()
  652.  
  653.  
  654.  
  655.  
  656.  
  657.  
  658.  

On obtient les résultats suivants :

-------------------------------------
   Nombre d'occurrences de chaque    
configuration de la population finale
     (diversité de la population)    
-------------------------------------
poids maximum =  269
-------------------------------------
 poids,profit : occurrences
-------------------------------------
384,310 :   1    
368,297 :   1    
357,296 :   1    
269,295 :  27  * 
-------------------------------------
Note : les solutions sont les configurations
de la population finale en dessous de la    
limite de poids autorisée

Soit 27 fois l'optimum global, tout dépend bien entendu des choix aléatoires faits par l'algorithme.

 

Sur les deux graphiques ci-dessus, on peut observer :

!!! Attention !!!

Dans l'implantation de l'algorithme génétique que j'ai donnée, le remplacement consiste à remplacer le père ou la mère si le meilleur enfant est meilleur que son père ou sa mère.

Il peut être plus judicieux de remplacer dans la population, l'individu de score le plus faible.

6.3. Formulation Minizinc

Le code Minizinc correspondant à la résolution de ce problème est :

sad.mzn

  1. %% ========================================================
  2. %% Auteur: Jean-Michel Richer
  3. %% email: jean-michel.richer@univ-angers.fr
  4. %% ========================================================
  5. %%
  6. %% Problème du sac à dos :
  7. %%
  8. %%    Etant donné un ensemble d'objets pesant un certain
  9. %%    poids (weight) et apportant un certain profit (profit)
  10. %%    on cherche à trouver quels objets mettre dans le sac
  11. %%    à dos de manière à obtenir le profit maximum tout en
  12. %%    ne dépassant pas le contrainte de poids maximal (W_max)
  13. %%
  14. %% ========================================================
  15.  
  16. include "globals.mzn";
  17.  
  18. %% --------------------------
  19. %%         Variables
  20. %% --------------------------
  21.  
  22. % maximum number of articles
  23. int: N = 10;
  24. % maximum weight
  25. int: W_max = 269;
  26.  
  27. array[1..N] of int: profit;
  28. array[1..N] of int: weight;
  29. array[1..N] of var 0..1: x;
  30.  
  31. profit = [55,10,47,5,4,50,8,61,85,87] ;
  32. weight = [95,4,60,32,23,72,80,62,65,46] ;
  33.  
  34. %% --------------------------
  35. %%        Constraints
  36. %% --------------------------
  37.  
  38. constraint sum(i in 1..N)(weight[i] * x[i]) <= W_max;
  39.  
  40. %% --------------------------
  41. %%          Search
  42. %% --------------------------
  43.  
  44. var int: gain = sum(i in 1..N)(profit[i] * x[i]);
  45. solve  :: int_search(x, max_regret,indomain_split, complete) maximize  gain;
  46.  
  47. %% --------------------------
  48. %%           Result
  49. %% --------------------------
  50.  
  51. output ["x = ", show(x), " ", show(gain)];
  52.  
  53.