Alignement par paires (Pairwise Sequence Alignment)

  Enumération exhaustive
Ainsi que nous l'avons vu précédemment, on cherche à obtenir un alignement de coût optimal. La méthode de recherche la plus simple et qui vient tout de suite à l'esprit consiste à réaliser une énumération de tous les alignments possibles et à retenir ceux de coût optimal. Malheureusement le nombre d'alignements différents de deux séquences de même longueur n est donné par la formule :

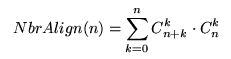
  Programmation dynamique
La Programmation Dynamique est la méthode la plus intéressante pour l'alignement de deux séquences car sa complexité temporelle et spatiale est en O(n²).

La Programmation Dynamique est appliquée à des problèmes d'optimisation pour lesquels un choix doit être fait entre plusieurs solutions possibles afin d'aboutir à une solution optimale. Le terme Programmation fait ici référence à une méthode basée sur le calcul de tableaux de valeurs.
Exemple d'application  

L'algorithme d'alignement global basé sur la programmation dynamique a été mis au point par Needleman et Wunsch en 1970 [1]. Une version pour l'alignement local fut ensuite introduite par Smith et Waterman en 1981 [2].

Soient deux séquences S = { x₁, x₂, ... , x_N } et T = { y₁, y₂, ... , y_M } à aligner. L'algorithme d'alignement utilise deux matrices de dimensions (N+1) x (M+1) :

• M[0..N,0..P] : la matrice des scores optimaux d'alignement qui stocke le coût des meilleurs alignements intermédiaires. Au final M[N,P] contient le coût du meilleur alignement global suivant w.
• Dir[0..N,0..P] : la matrice des directions qui indique la suite d'opérations d'édition à réaliser afin d'obtenir un alignement optimal.

• calcul des matrices M et Dir
• création d'un alignement optimal par lecture de la matrice des directions

Remarque : la matrice des directions n'est pas essentielle car elle peut être déduite de la matrice des scores optimaux d'alignement, mais pour des raisons de simplicité d'écriture des algorithmes on utilise généralement cette matrice.

• Première étape : calcul de M et Dir
  
  

  Soient deux indices i, j tels que i,j >= 1. Supposons que nous ayons aligné les préfixes suivants par rapport à une fonction de score w :

  • (1) S[1..i-1] avec T[1..j-1] de score global M[i-1,j-1],
  • (2) S[1..i-1] avec T[1..j] de score global M[i-1,j],
  • (3) S[1..i] avec T[1..j-1] de score global M[i,j-1].
  
  Un alignement de S[1..i] avec T[1..j] est obtenu :
  • à partir de (1) suivi d'un appariement ou un remplacement de x_i-1 avec y_j-1
    de score M[i-1,j-1] + w(x_i-1,y_j-1)
  • à partir de (2) suivi d'une insertion dans T : (x_i,-)
    de score M[i-1,j] + w(x_i-1,-)
  • à partir de (3) suivi d'une insertion dans S : (-,y_j)
    de score M[i,j-1] + w(-,y_j-1)
  
  On voit donc que le calcul de M[i,j] dépend de M[i-1,j-1], M[i-1,j] et M[i,j-1] comme suit :
  
  

  M[i-1][j-1]		M[i-1,j]
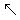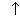  M[i,j-1]		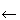M[i,j]

Alignement par Paires par Programmation Dynamique

Soient deux séquences S et T de longueurs respectives N et P. La recherche d'un alignement global optimal entre S et T suivant une fonction de score w est obtenu par construction d'une matrice des scores optimaux d'alignement M[0..N,0..P] telle que : initialisation : M[0,0] = 0 M[i,0] = M[i-1,0] + w(xi,-)   pour tout i de 1 à N M[0,j] = M[0,j-1] + w(-,yj)   pour tout j de 1 à P calcul du score optimal : M[i,j] = optimise M[i-1,j-1] + w(xi,yj) M[i-1,j] + w(xi,-) M[i,j-1] + w(-,yj) où M[i,j] représente le score de l'alignement de S[1..i] avec T[1..j] et optimise est la fonction : maximum si w est une matrice de score maximisante minimum si w est une matrice de score minimisante La matrice des directions est obtenue par les formules suivantes : initialisation : Dir[0,0] = x Dir[i,0] =   pour tout i de 1 à N Dir[0,j] =   pour tout j de 1 à P calcul des directions : Dir[i,j] = Union si M[i,j] = M[i-1,j-1] + w(xi,yj) si M[i,j] = M[i-1,j] + w(xi,-) si M[i,j] = M[i,j-1] + w(-,yj)

• Deuxième étape : création d'un alignement
  
  

  Une fois les matrices M et Dir obtenues, il suffit pour trouver un alignment de parcourir le chemin inverse depuis M[N,P] en remontant vers M[0,0] en se déplaçant dans l'une des trois directions possibles (Nord, Ouest ou Nord-Ouest) uniquement si le mouvement est autorisé par la matrice des directions.

  On obtient donc non pas un alignement unique mais un ensemble d'alignements possibles. On peut se limiter à un seul alignement en ne choisissant qu'une direction à chaque étape et en privilégiant une direction en particulier.
  Exemple d'application  

Remarque finale : le problème d'alignement est un problème difficile car on ne sait pas définir en terme qualitatif ce qu'est un bon alignement. L'alignement concerne la séquence primaire or pour juger de la qualité d'un alignement il faudrait pouvoir disposer d'informations supplémentaires concernant la structure secondaire (voire tertiaire) des séquences afin d'aligner des structures de même type (on peut penser qu'il est plus judicieux d'aligner une hélice alpha avec une autre hélice alpha et non pas avec un feuillet béta).

Sommaire