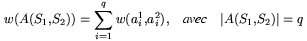• des insertions d'un nucléotide ou d'un ensemble de nucléotides,
• des suppressions d'un nucléotide ou d'un ensemble de nucléotides,
• des substitutions d'un nucléotide par un autre nucléotide.

• l'identité : deux séquences sont dites identiques si elles se correspondent parfaitement. La notion d'identité fait également référence au pourcentage de résidus identiques en regard dans un alignement,
• la similarité : deux séquences sont dites similaires si elles sont relativement proches sans toutefois être identiques,
• l'homologie est un cas particulier de similarité dans lequel on considère que deux séquences similaires dérivent d'un ancêtre commun, c'est-à-dire que les séquences sont des évolutions d'une séquence initiale commune pour laquelle certaines parties ont été ajoutées, supprimées ou remplacées.

Matrice de score

L'opération d'alignement consiste à faire apparaître le possible cheminement d'une évolution d'une séquence par rapport à une autre ou des deux séquences par rapport à un hypothétique ancêtre commun.

L'opération d'alignement consistera donc à mettre en regard les caractères de deux séquences S₁ et S₂ de manière à ce que les séquences se correspondent le mieux possible. Les séquences n'étant de manière générale pas strictement identiques on autorise le décalage des caractères en insérant des espaces (ou gap) dans les séquences.

Un alignement peut être construit grâce à quatre opérations de base :

• l'appariement (match) : (a,a), un caractère de la première séquence est mis en regard d'un caractère identique dans la deuxième séquence,
• la substitution : (a,b), un caractère de la première séquence est mis en regard d'un caractère différent dans la deuxième séquence,
• l'insertion d'un gap dans S₁ : (-,b)
• l'insertion d'un gap dans S₂ : (a,-)

Remarque : l'insertion dans une séquence peut également être considérée comme une suppression (ou deletion en anglais) dans la séquence en regard. On parle alors d'opérateurs d'indel (INsertion-DELetion).

Afin de déterminer le ou les meilleur(s) alignment(s), on attribue un coût à chaque opération d'alignement suivant une matrice de score (notée w) et on tente d'optimiser le coût de l'ensemble de ces opérations. Un exemple simple de matrice de score est la matrice identité :

Le score w(-,-) n'est pas défini puisque ce cas de figure n'est pas autorisé pour l'alignement par paires. On peut également modifier les coefficients afin de favoriser l'une des opérations d'édition. Par exemple si on utilise la matrice identité on cherche à favoriser les appariements et à minimiser les insertions de gaps.

On peut distinguer 2 types de matrices de score :

• les matrices de score maximisantes (ou mesures de similarité) pour lesquelles le score d'un appariement est supérieur aux autres scores : w(a,a) > w(a,b), w(a,-), w(-,a)
• les matrices de score minimisantes (ou mesures de distance) pour lesquelles le score d'un appariement est inférieur aux autres scores : w(a,a) < w(a,b), w(a,-), w(-,a)

Dans le cas des protéines il existe des matrices spécifiques :

• PAM (Percent Accepted Mutation), introduite par Dayhoff et al. pour quantifier les changements qui interviennent dans une séquence de protéine. Cette étude est basée sur 1572 protéines issues de 71 familles. La matrice la plus couramment utilisée est PAM 250.
• BLOSUM (Blocks Substitution Matrices), introduite par Henikoff et pout laquelle on observe la fréquence de variation de blocks obtenus apr des alignements locaux. Cette étude est basée sir des alignements provenant de la base de données BLOCKS. La matrice la plus couramment utilisée est BLOSUM 62 ce qui correspond à des protéines n'ayant pas plus de 62% d'identité.
• Gonnet.

Définition - Somme des paires

Le score d'un alignement par paires A(S1,S2) est donné par une formule comme par exemple la fonction de somme des paires (Sum of Pairs) :

Sommaire