 |
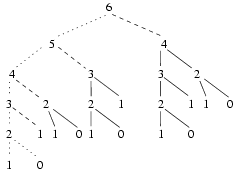
Sur cet exemple on voit que pour calculer Fib(6),
il faut calculer Fib(5) puis Fib(4). Or, lors du calcul de Fib(5)
on évalue déjà Fib(4). On calculera donc 2 fois Fib(4). |
| Exemple de calcul pour Fibonacci de 6 |
| Recherche en Bioinformatique - Programmation dynamique |
| Algorithme 1 |
Fonction Fib1(n : entier) : entier debut si n <= 1 alors retour n; retour Fib1(n-1) + Fib1(n-2); fin |
| Algorithme récursif pour le calcul de la suite de Fibonacci |
 |
Sur cet exemple on voit que pour calculer Fib(6),
il faut calculer Fib(5) puis Fib(4). Or, lors du calcul de Fib(5)
on évalue déjà Fib(4). On calculera donc 2 fois Fib(4). |
| Exemple de calcul pour Fibonacci de 6 |
| Algorithme 2 |
Fonction Fib2(n : entier) : entier debut si n = 0 alors retour 0; si tab[n] != 0 alors retour tab[n]; tab[n] = Fib1(n-1) + Fib1(n-2); retour tab[n]; fin |
|
Algorithme récursif pour le calcul de la suite de Fibonacci avec stockage des valeurs intermédiaires dans un tableau |
| Algorithme 3 |
Fonction Fib3(n : entier) : entier
debut
tab[0] = 0;
tab[1] = 1;
pour i = 2 à n faire
tab[i] = tab[i-1] + tab[i-2];
fpour
retour tab[n];
fin
|
|
Algorithme pour le calcul de la suite de Fibonacci avec calcul progressif |
| n | Fib1 | Fib2 ou 3 |
| 10 | 1s < | 1s < |
| 20 | 1s < | 1s < |
| 30 | 1s < | 1s < |
| 40 | 10s | 1s < |
| 50 | 20m | 1s < |
| 60 | 42h27m | 1s < |
| Temps d'exécution sur serveur Helios | ||
Jean-Michel Richer, 2004