Gagne Ton Papa
1.1. Objectif
Le jeu Gagne Ton Papa consiste à résoudre des casse-tête en deux ou trois dimensions utilisant des formes en 3 dimensions.
Pour ce qui nous concerne, nous allons nous intéresser à la résolution de casse-tête en deux dimensions.
- dans un premier temps, on désire obtenir un algorithme de résolution qui fournit toutes les solutions
- dans un second temps, on aimerait disposer d'une interface graphique qui affiche les solutions à mesure qu'on les trouve
1.1.1. Exemple de résultat attendu
Proposez un programme Python qui recherche et affiche toutes les solutions lorsqu'on lui passe comme fichier un défi sous la forme :
defi_1.txt <-- nom du fichier
----------
4 <--- penta-4
LMarron <-- liste des pièces suivant leur nom
SBleu
CJaune
...
Voici un exemple d'interface utilisant la librairie pygame de Python :
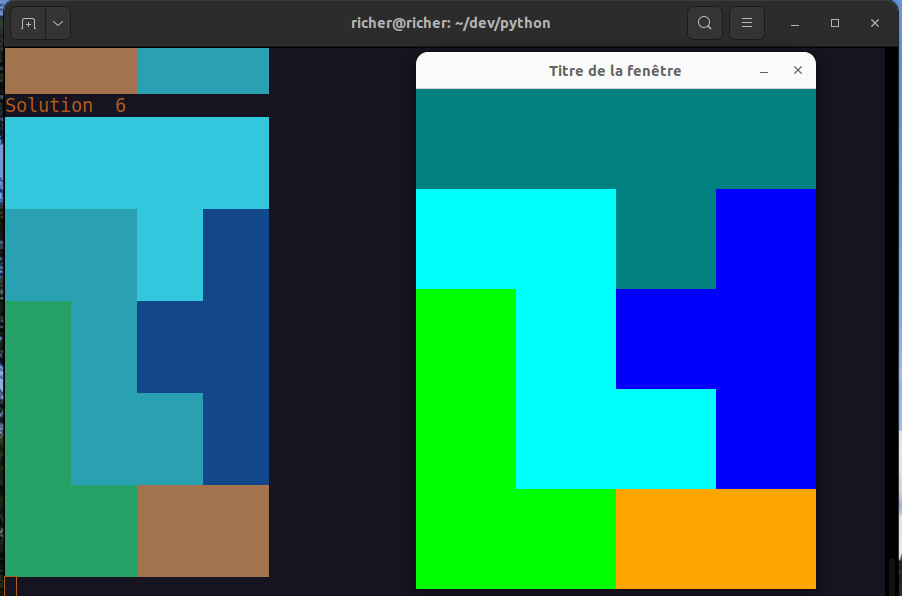
1.2. Recherche de toutes les solutions
1.2.1. Les pièces
Elles sont au nombre de 18 :
- deux points (1,1) de couleur rouge (PointRouge, red)
- un point (2,2) de couleur violette (PointViolet, magenta)
- un b de couleur rose (BRose, pink)
- un c de couleur jaune (CJaune, yellow)
- des i dont :
- deux i (2,1) de couleur orange clair (IOrangeClair, lightorange)
- un i (3,1) de couleur orange foncé (IOrangeFonce, darkorange)
- un i (4,1) de couleur rose (IRose, pink)
- quatre L :
- un L (2,2) marron (LMarron, maroon)
- un L (3,2) bleu clair (LVert, green)
- un L (3,3) bleu foncé (LBleu, blue)
- un L (4,2) orange foncé (LOrangeFonce, darkorange)
- deux T :
- un T (4,2) marron (TMarron, maroon)
- un T (2,3) bleu clair (TBleuClair, lightblue)
- trois S :
- un S (2,3) jaune (SJaune, yellow)
- un S (3,3) bleu clair (SBleuClair, lightblue)
- un S (2,4) violet (SViolet, magenta)
1.2.2. Modélisation
L'aire de jeu dans laquelle on va positionner les pièces est modélisée sous forme d'une matrice $5 × N$ où $N$ vaut 3, 4, 5 ou 6. On pourra utiliser la librarie numpy pour représenter les matrices.
On modélise ensuite les pièces du jeu sous forme 2D.
une pièce (par exemple CJaune) sera définie par :
- son nom "CJaune"
- sa couleur sous forme de chaine de caractères "yellow" qui correspondra à un nom de couleur HTML
- un identifiant sous forme d'une puissance de 2 ce qui permettra de différencier les pièces lorsqu'on va les placer sur l'aire de jeu
chaque pièce est composée de plusieurs formes qui correspondent aux différentes rotations (0, 90°, 180°, 270°) ainsi que le flip qui consiste à retourner la pièce. Certaines pièces n'auront au final qu'une seule forme ou 2, ou 4 ou 8.
Une forme sera composée :
- d'une matrice de $y$ lignes et $x$ colonnes ainsi que de 0 ou de 1 qui correspondent au fait que dans la matrice une case est vide (0) ou pleine (1) :
Voici par exemple deux des quatre formes de CJaune :
|
3 lignes x 2 colonnes
|
2 lignes x 3 colonnes
|
Modélisez l'ensemble des pièces et de leurs formes et les stocker dans une BoiteDePieces.
1.2.3. Algorithme
Proposez un algorithme récursif avec retour-arrière (backtrack) qui permet de trouver toutes les solutions. La relation de récurrence est la suivante :
- condition d'arrêt : si on a pu placer toutes les pièces, on dispose d'une solution, il faut donc l'afficher et incrémenter le nombre de solutions trouvées
- récurrence : sinon pour chaque case $C$ de l'aire de jeu et pour chaque pièce $P$, si $P$ peut être placée en $C$ alors la placer et relancer la recherche avec les pièces restantes
1.3. Travail
1.3.1. Implantation des pièces
Vérifier que les pièces s'affichent correctement, on implantera deux fonctions :
- placer(aire_de_jeu,y,x,forme) qui place une forme en coordonnées $(y,x)$ dans une aire de jeu
- afficher(aire_de_jeu) qui affiche le contenu d'une aire de jeu
1.3.2. Lecture d'un défi
1.3.3. Algorithme de recherche
1.3.4. Interface graphique
On pourra s'inspirer par exemple du jeu de Pong.
1.4. Concours
Le gagnant sera celui qui aura proposé le projet le plus abouti et qui le nombre correct de solutions pour des défis donnés.