3. C++ et le monde extérieur
- Introduction au C++ (1 jour)
- C++ avancé (2 jours)
- C++ et le monde extérieur (1 jour)
Cours
- Boost
- OpenMP, TBB, MPI et programmation parallèle
- Librairies dédiées au calcul scientifique (BLAS, LAPACK, MKL, GSL, PETSc)
- Interopérabilité avec les bases de données
- Interopérabilité avec Python
- Interopérabilité avec Perl
- thrust
- tests : cppunit, googletest
- Web services et GSOAP
- Compiler des librairies externes
Exercices
Exercice 3.1
Ecrire un programme qui calcule la valeur de PI en utilisant un calcul d'intégrale entre 0 et 1 de la fonction :
$$f(x) = 4 / (1 + x^2)$$
Modifier le programme pour obtenir une version OpenMP.
Exercice 3.2
Ecrire un programme qui calcule la valeur de PI en utilisant la méthode de Monte Carlo. On considère un carré qui englobe un cercle de rayon 1. On lance de manière aléatoire des fléchettes dans cet espace carré. La probabilité pour qu'une fléchette soit dans le cercle est proportionelle aux aires du cercle et du carré :
- Aire(cercle) = π × r2
- Aire(carré) = (2× r)2
- ratio = Aire(cercle) / Aire(carré) = π / 4;
Utiliser OpenMP.
Exercice 3.3
Comparer le produit de matrices dans sa version classique et sa version OpenMP.
Par exemple sur un Quad Core i5 4570, on obtient les résultats suivants :
| dimension | classique | 2 threads | 4 threads | 8 threads |
| 2000 | 17 | 8 | 4 | 5 |
| 4000 | 175 | 77 | 60 | 62 |
Exercice 3.4
Utiliser la méthode des rectangles pour calculer l'intégrale de $f(x) = x^2$ entre 0 et 3.
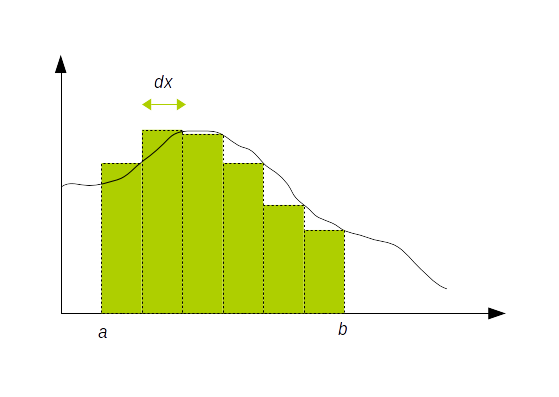
De manière générale si on doit intégrer la fonction $f(x)$ entre $a$ et $b$, on peut réaliser le calcul symbolique ou calculer l'aire de la courbe en la décomposant en $N$ petits rectangles (ou des trapèzes) :
$$ ∫_a^b f(x)\, dx = ∑↙{i=1}↖N f(a + i × dx) × dx $$
double dx = (b - a) / N;
double aire_totale = 0;
for (int i=1; i <= N; ++i) {
double aire = f(a + i * dx) * dx;
aire_totale += aire;
}
Exercice 3.5
Si on utilise $P$ threads (OpenMP) ou $P$ processeurs (MPI) chaque thread calculera l'aire de $N / P$ rectangles.
- $T_0$ de $a$ à $a + (N/P) × dx$
- $T_1$ de $a + N/P × dx$ à $a + (2N/P) × dx$
- ...
- $T_{P-1}$ de $a + ((P-1)N)/P × dx$ à $a + (N P)/P × dx$
Donnez une solution OpenMP de l'exercice précédent
Exercice 3.6
Donnez une solution MPI de l'exercice précédent.
Exercice 3.7
Ecrire un programme qui teste le temps de calcul de différents algorithmes pour la somme et le produit de matrices génériques avec une implantation utilisant la classe valarray de la STL :
- implantation 1 de la somme : utiliser l'algorithme transform
- implantation 2 de la somme : utiliser $z = x + y$ où $x$ , $y$ et $z$ sont des valarray
- implantation 1 du produit : utiliser l'algorithme issu de la traduction de la formule générale $c_i^j = ∑_k a_i^k * b_k^j$
- implantation 2 du produit : paralléliser l'implantation 1 avec OpenMP
- implantation 3 du produit : utiliser la technique du tiling (tuilage) avec une taille de 32 (les matrices devront avoir des dimensions multiples de 32 dans ce cas)
- implantation 4 du produit : paralléliser l'implantation 3 avec OpenMP
- implantation 5 du produit : proposer d'utiliser la fonction optimisée blas_dgemm avec l'une des librariries BLAS, GSL ou MKL
On redéfinira les opérateurs + et * pour la classe Matrix<T>.
On fournira un fichier de compilation automatique makefile
Voir la solution complète archive