Cette page fait partie du cours de polytech PeiP1 et 2 Bio

11. Mise en pratique : Réseaux de Neurones

11.1. Introduction

Les Réseaux de Neurones ou Neural Networks sont une technologie ancienne dont les premiers travaux remontent à 1943 avec les travaux de McCulloch et Pitts.

Le réseau de neurones tente de modéliser le fonctionnement du cerveau au travers de neurones artificiels qui modélisent le fonctionnement de nos neurones cérébraux, ou tout du moins la vision que nous en avons.

Voici quelques références introductives concernant les réseaux de neurones :

• Réseaux de neurones
• What is a Neural Network ? (Vidéo)
• Introducing Deep Learning and Neural Networks for rookies
• Multi-Layer Neural Networks with Sigmoid Function
• Neural Networks Tutorial

11.2. Installation des packages

Pour que keras et tensorflow fonctionnent, il faut utiliser (Mai 2021) une version 3.6 de Python. Je conseille donc la procédure suivante sous Windows (et qui fonctionne également sous Linux) qui crée un environnement spécifique :

Dans le menu de Windows, chercher l'application Anaconda prompt et l'exécuter. Dans la console qui s'ouvre, taper les commandes suivantes et répondre 'y' à chaque fois que cela est demandé :

# Créer un environnement avec Python en version 3.6
# appelé nn pour Neural Network
(base)> conda create --name nn python=3.6

Vous devriez obtenir la sortie suivante :

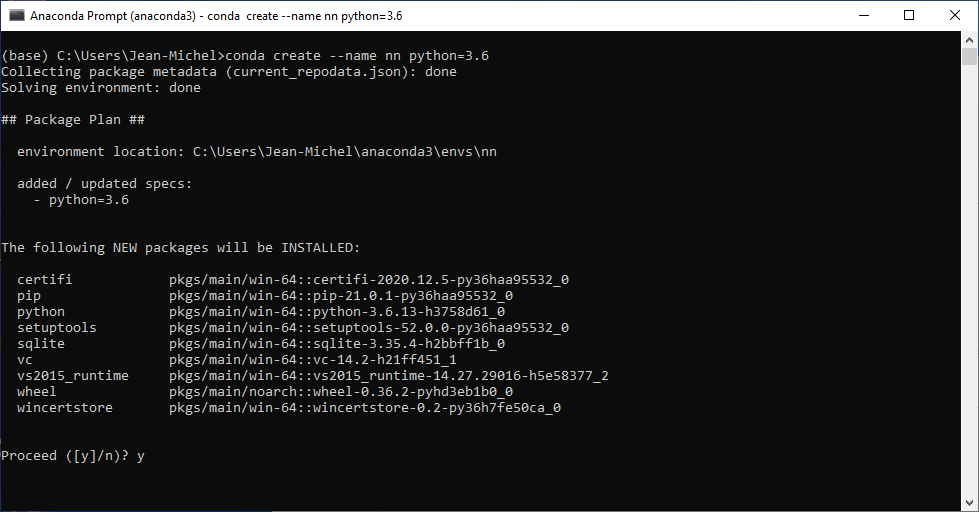
Puis on installe les packages :

# rendre l'environnement nn actif
(base)> conda activate nn
# on vérifie qu'on a la bonne version de Python
(nn)> python --version
Python 3.6.13 :: Anaconda, Inc.

# on installe les packages requis pour l'environnement nn
(nn)> conda install numpy matplotlib seaborn pandas
(nn)> conda install scikit-learn
(nn)> conda install keras

Vous devriez avoir les packages sous les versions suivantes :

• keras 2.3.1
• matplotlib 3.3.4
• numpy 1.19.2
• pandas 1.1.3
• scipy 1.5.2
• seaborn 0.11.1
• tensorflow 2.1.0

Pour le vérifier, il suffit de saisir la commande conda list dans Anaconda prompt.

Enfin, pour pouvoir utiliser cet environnement avec Thonny, il faut modifier l'interpréteur comme sur l'image suivante (remplacez 'Jean-Michel' par votre nom utilisateur) :

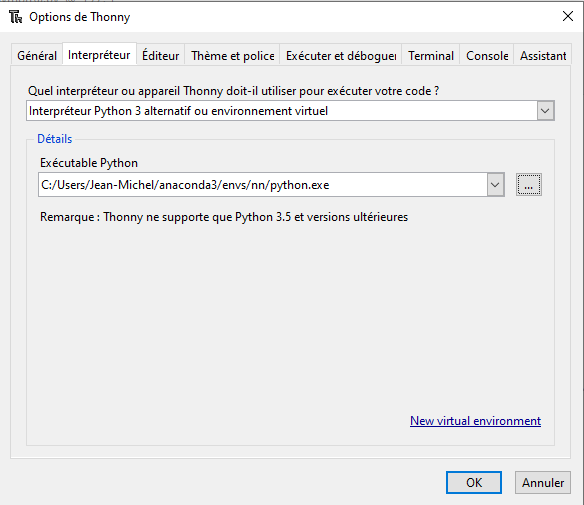
Tout devrait fonctionner normalement. Si vous rencontrez un problème avec tensorflow / keras, essayez d'ajouter le code suivant en début de programme ce qui empêche l'utilisation de la carte graphique en cas de problème de compatibilité matérielle :

import os
os.environ['CUDA_VISIBLE_DEVICES'] = '-1'

11.3. Application

11.3.1. Les données

Nous allons créer un réseaux de neurones capable de prédire le diabète chez les indiens Pimas.

Les Pimas sont une une tribu d'Amérindiens vivant en Arizona et qui présente les plus forts taux d'obésité et de diabète de tous les États-Unis : record du monde du diabète de type 2 avec 50% de la population (contre 9% pour les blancs américains), âgée de plus de 35 ans. Certains attribuent cette obésité au fait que les Pimas n'ont plus la même alimentation qu'auparavant, pour d'autres il s'agit de facteurs génétiques.

Le fichier de données contient les informations suivantes pour chacune des 768 femmes de l'étude :

1. Number of times pregnant (preg)
2. Plasma glucose concentration a 2 hours in an oral glucose tolerance test (plas)

   • for prediabetes : 40–199 mg/dL
   • for diabete :200 mg/dL or greater
3. Diastolic blood pressure (mm Hg) (pres)
4. Triceps skin fold thickness (mm) (skin)
5. 2-Hour serum insulin (mu U/ml) (insu)
6. Body mass index (weight in kg/(height in m)^2) (bmi) indice de masse corporelle ou IMC : surpoids (25 à 30), obésité modérée (30 à 35), obésité sévère (35 à 40)
7. Diabetes pedigree function (pedi)
8. Age (years) (age)
9. testé positif ou non au diabète (class)

11.3.2. Chargement des données et ajustements

On commence par charger les données avec pandas sous forme d'un DataFrame, puis on affiche les premières lignes du fichier :

   preg  plas  pres  skin  insu   bmi   pedi  age            class
0     6   148    72    35     0  33.6  0.627   50  tested_positive
1     1    85    66    29     0  26.6  0.351   31  tested_negative
2     8   183    64     0     0  23.3  0.672   32  tested_positive
3     1    89    66    23    94  28.1  0.167   21  tested_negative
4     0   137    40    35   168  43.1  2.288   33  tested_positive
shape= (768, 9)

11.3.2.a  Remplacement des données textes en données numériques

Toutes les données sont au format numérique sauf la dernière colonne, on va donc la remplacer par des valeurs numériques :

• tested_positive est remplacé par 1
• tested_negative est remplacé par 0

rn_pimas_load_data.py

11.3.2.b  Examen des données

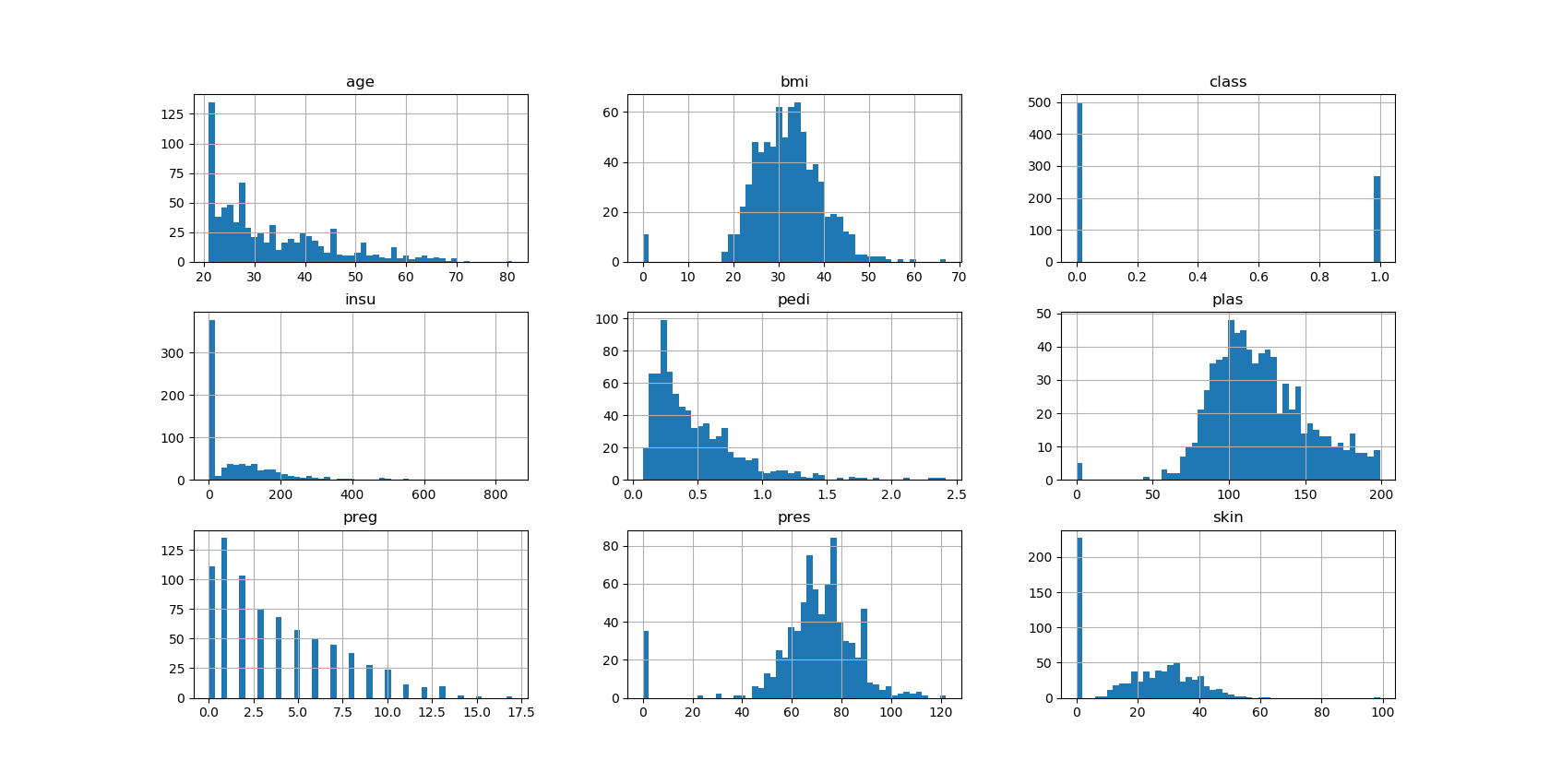
On examine ensuite les données en affichant un sommaire des données numériques ainsi qu'un graphique des distributions des données :

            preg        plas        pres  ...        pedi         age       class
count  768.000000  768.000000  768.000000  ...  768.000000  768.000000  768.000000
mean     3.845052  120.894531   69.105469  ...    0.471876   33.240885    0.348958
std      3.369578   31.972618   19.355807  ...    0.331329   11.760232    0.476951
min      0.000000    0.000000    0.000000  ...    0.078000   21.000000    0.000000
25%      1.000000   99.000000   62.000000  ...    0.243750   24.000000    0.000000
50%      3.000000  117.000000   72.000000  ...    0.372500   29.000000    0.000000
75%      6.000000  140.250000   80.000000  ...    0.626250   41.000000    1.000000
max     17.000000  199.000000  122.000000  ...    2.420000   81.000000    1.000000

Par exemple, pour le nombre de grossesses, celui-ci varie de 0 à 17 !

rn_pimas_examine.py

11.3.2.c  Traitement des données manquantes

On note donc que les colonnes bmi, insu, plas, pres, skin possèdent des valeurs à 0 alors que ce ne devrait pas être le cas.

rn_pimas_fill_missing.py

11.3.2.d  Données d'apprentissage

Finalement, on crée les données d'apprentissage en séparant le DataFrame initial en la matrice des données d'apprentissage $X$ et la propriété à prédire $y$ :

• $X$ prend en compte les 8 propriétés suivantes : preg, plas, pres, skin, insu, bmi, pedi, age
• $y$ représente la présence ou non de diabète (class)

rn_pimas_learning_data.py

11.3.3. Création et apprentissage du réseau de neurones

A présent, la partie la plus sybilline commence.

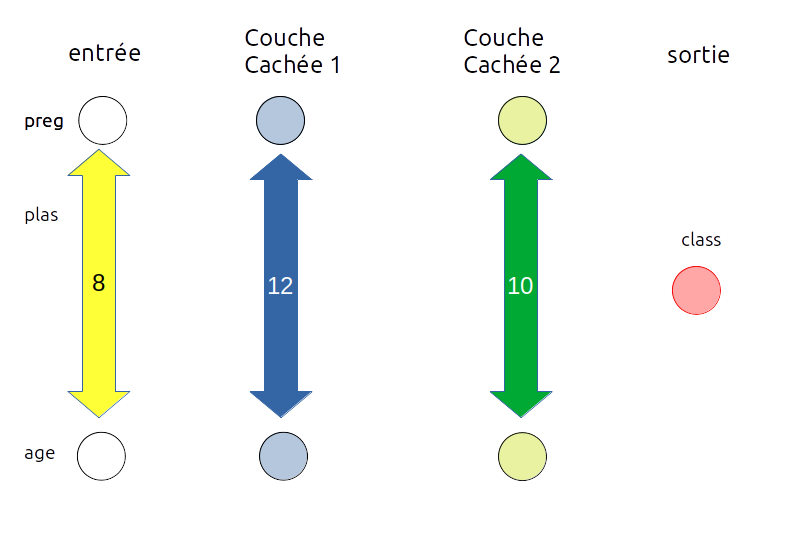
Nous utilisons Keras qui est une interface qui simplifie la création des RN. On met en place le réseau suivant :

• la couche d'entrée est composée de 8 neurones car chaque individu est caractérisé par 8 propriétés
• on crée ensuite deux couches cachées (hidden layers) :
  • une première couche de 12 neurones
  • une deuxième couche de 10 neurones
• la couche de sortie est composée d'un neurone qui correspond à la classe : est diabétique ou non

rn_pimas_create_nn.py

rn_pimas_nn_learning.py

On définit trois paramètres (compile):

• la fonction a optimiser : binary_crossentropy
• l'optimiseur : adam
• les valeurs que l'on désire enregistrer et qui permettront de générer des graphiques : accuracy et mse (mean squared error)

Là, également, le choix est laissé libre à l'utilisateur de paramétrer son réseau :

• pour ce qui touche aux fonctions de perte (loss function), on pourra consulter ce site qui passe en revue les différentes fonctions : pour le problème qui nous intéresse, il est recommandé d'utiliser la fonction Binary Cross-Entropy, puis pour la couche de sortie, une sigmoïde.
• concernant les optimiseurs, on a le choix entre :
  • Adam, Adagram, Adadelta, Adamax
  • SGD (Stochastic Gradient Descent)
  • RMSProp
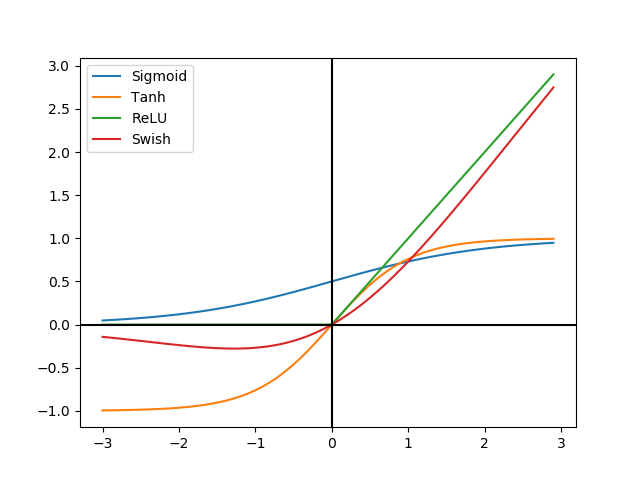
• pour les fonctions d'activation :
  • linear, elu (Exponential linear Unit), relu (Rectified Linear Unit), selu (Scaled Exponential Linear Unit)
  • softmax, softplus, softsign
  • exponential, tanh (tangente hyperbolique), sigmoid
• pour le nombre d'epoch, il faut choisir une valeur entre 500 et 5000 dans le cas présent.

11.3.4. Résultat et précision du RN

On récupère les informations liées à l'apprentissage du RN (evaluate) et on les affiche :

rn_pimas_precision.py

# pour 8000 epochs
loss = 0.0335
accuracy = 98.6979 %
mse = 0.0094

Les graphiques qui correspondent aux données enregistrées (mse, accuracy) sont les suivants :

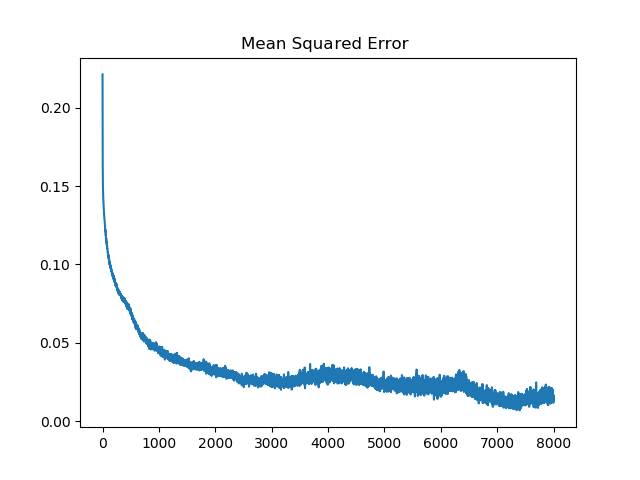
Progression Mean Squared Error (8000 epochs)

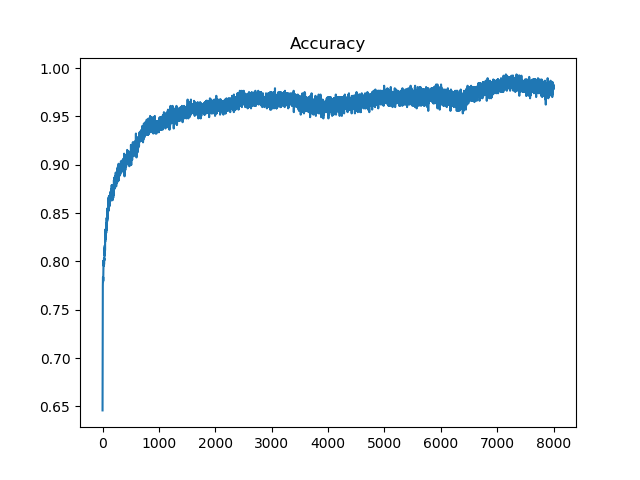
Progression précision (Accuracy, 8000 epochs)

On remarque que $mse ≈ 1 / { accuracy}$, i.e. plus l'erreur est faible, meilleure est la précision.

Enfin, on essaye de réaliser la prédiction sur $X$ à partir du RN et on compare à ce qu'on devrait avoir, c'est à dire $y$ :

rn_pimas_prediction.py

expected=1, found=0
expected=0, found=1
expected=0, found=1
expected=1, found=0
expected=0, found=1
expected=1, found=0
expected=0, found=1
expected=1, found=0
expected=0, found=1
expected=1, found=0

11.3.5. Amélioration de la prédiction

Peut-on améliorer la prédiction ?

11.3.5.a  Normalisation / Standardisation

rn_pimas_normalization.py

On place donc la normalisation des données avant la création du réseau de neurones.

11.3.5.b  Batch_size

Sur un AMD Ryzen 5 3600 doté d'une carte graphique GTX 1070 les temps de calcul pour 8000 epochs en fonction de la variable batch_size sont de :

• GPU :
  • batch_size = 16 : 664 s (accuracy = 94.5312)
  • batch_size = 32 : 341 s (accuracy = 99.7396)
  • batch_size = 64 : 174 s (accuracy = 95.0521)
  • batch_size = 128 : 92 s (accuracy = 97.3958)
  • batch_size = 256 : 50 s (accuracy = 95.0521)
  • batch_size = 384 : 37 s (accuracy = 93.4896)
  • batch_size = 768 : 23 s (accuracy = 93.4896)
• CPU :
  • batch_size = 5 : 868 s (accuracy = 89.9740)
  • batch_size = 8 : 549 s (accuracy = 92.4479)
  • batch_size = 10 : 440 s (accuracy = 95.7031)
  • batch_size = 16 : 279 s (accuracy = 97.2656)
  • batch_size = 32 : 147 s (accuracy = 99.7396)
  • batch_size = 64 : 77 s (accuracy = 98.1771)
  • batch_size = 128 : 40 s (accuracy = 96.8750)
  • batch_size = 256 : 23 s (accuracy = 94.7917)
  • batch_size = 384 : 18 s (accuracy = 94.0104)
  • batch_size = 768 : 12 s (accuracy = 94.6615)

Dans le cas présent, on obtient une meilleure prédiction avec un batch_size = 32.