Cette page fait partie du cours de polytech PeiP1 et 2 Bio

9. Mise en pratique : Régressions Linéaires

9.1. Introduction

9.1.1. Fouille de données

On s'intéresse dans ce TP à la Fouille de Données (Data Mining) qui est un domaine de l'informatique qui, à partir d'ensembles de données brutes, tente d'établir des relations entre les données dans le but d'extraire des connaissances enfouies et donc non visibles à l'oeil nu ou que l'on ne peut déduire facilement car la relation qui lie les données est complexe.

Le manque de visibilité tient généralement au fait qu'il est difficile de voir ces relations d'autant plus que le volume de données est important.

Dans ce genre d'étude on considère un ensemble de données sous forme d'une matrice $D$ qui correspondent à $N$ individus ou objets (lignes de la matrice) décrits par $K$ propriétés ou colonnes ($P_1, ..., P_K$).

Parmi ces propriétés, on distingue :

Parmi les propriétés utiles $X$, on tente généralement de prédire l'une d'entre elles appelée la cible $y$ (target) en fonction des autres et que l'on va extraire de la matrice $X$.

La matrice initiale des données $D$ est donc composée des données inutiles $I$, des données utiles à l'établissement de la relation $X$ et de la cible $y$ :

$$ D(N,K) = [ X(N,K-Z-1), y(N,1), I(N,Z) ] $$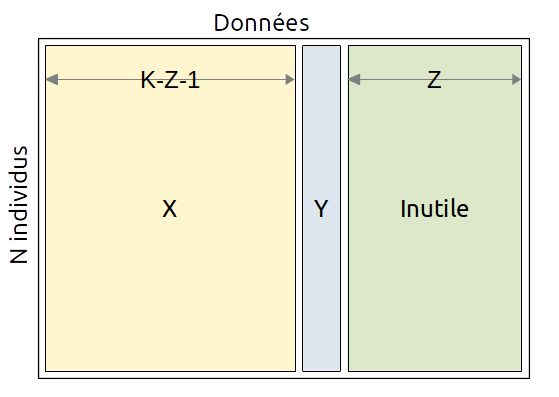

On cherche alors à trouver une fonction / relation $f$ telle que :

$$ y ≈ f(X) $$

Une fois $f$ déterminée on pourra calculer $y' = f(X)$ et comparer $y$ à $y'$ afin de déterminer si $f$ établit bien une relation dès lors que $|y - y'|^2$ est proche de 0.

On pourra consulter ce document pour comprendre comment on trouve les coefficients de la droite.

9.1.2. Régression linéaire

La régression linéaire est un procédé simple qui permet de vérifier que des données sont corrélées, c'est à dire qu'elles sont liées par une relation linéaire du type $y = ax + b$.

La régression linéaire avec deux variables $(x,y)$ peut être étendue à plusieurs variables, on parle alors de régression linéaire multiple : $y = a_1 x_1 + a_2 x_2 + ... + a_n x_n + b$.

La droite ou l'hyperplan obtenu permet dans certains cas de classer (séparer) les données en deux classes, on parle alors de classifieur (issus de l'anglais classifier) mais le but de la régression est de rassembler les données plutôt que de les séparer. Nous verrons d'ailleurs que les SVM (Support Vector Machine) sont mieux adaptés à la classification.

En Apprentissage Automatique (Machine Learning) le rôle du classifieur est de classer dans des groupes (des classes) des données (individus) qui ont des propriétés similaires. Un classifieur linéaire est un type particulier de classifieur qui calcule la décision par combinaison linéaire des échantillons.

9.2. Régression linéaire simple

On considère un exemple simple de régression linéaire où à partir de données pour l'axe des $x$, on génère des points autour de la droite d'équation $y = 2x + 3$. La procédure à suivre est la suivante :

  1. définir la fonction $f(x) = 2x + 3$
  2. générer un vecteur $X$ de valeurs entre 1 et 20 par pas de 0.5 en utilisant numpy.arange
  3. générer le vecteur $y$ qui résulte de l'application de $f$ sur $X$ et auquel on ajoute des valeurs aléatoires entre -0.5 et +0.5 grâce à numpy.random.uniform
  4. utiliser la classe sklearn.linear_model.LinearRegression pour créer un modèle de régression :
    1. from sklearn.linear_model import LinearRegression
    2. modele = LinearRegression()
    3.  
  5. calculer le modèle grâce à la méthode fit de la classe. Attention il faut modifier la forme de $X$ pour en faire une colonne et non une ligne !
  6. afficher intercept_ et coeff_
  7. calculer $y'$ à partir du modèle de régression et de $X$
  8. afficher $y$ et $y'$ sur le même graphique
  9. afficher les informations statistiques du modèle :
    1. import statsmodels.api as sm
    2. X_stats = sm.add_constant(X)
    3. stats = sm.OLS(y, X_stats).fit()
    4. print(separator)
    5. print( stats.summary() )
    6.  

On obtiendra par exemple le résultat suivant :


==================================================
Rubriques (axe des x) :
==================================================
[ 1.   1.5  2.   2.5  3.   3.5  4.   4.5  5.   5.5  6.   6.5  7.   7.5
  8.   8.5  9.   9.5 10.  10.5 11.  11.5 12.  12.5 13.  13.5 14.  14.5
 15.  15.5 16.  16.5 17.  17.5 18.  18.5 19.  19.5]
==================================================
y à prédire :
==================================================
[ 5.09610762  6.02063373  7.20869107  7.55953374  8.69358316 10.45456651
 11.09560257 12.26032477 12.73454373 13.90524987 14.67045322 16.47500536
 17.21316613 18.23809807 18.70526737 19.57808864 21.22759304 21.61884707
 23.08646438 24.00087065 24.57424951 25.72739112 27.12351844 28.04040252
 29.078628   30.2117482  31.21699936 32.21579627 32.50008577 33.7951452
 35.35486701 35.7705316  36.73241912 38.40707455 38.91780429 40.15356994
 41.01813109 42.08555222]


 Calcul de la régresion... 


coefficients :  [2.00117446]
constante    :  2.9818198074834257



==================================================
Prédiction :  [ 4.98299427  5.9835815   6.98416873  7.98475596  8.98534319  9.98593042
 10.98651765 11.98710488 12.98769211 13.98827934 14.98886657 15.9894538
 16.99004103 17.99062826 18.99121549 19.99180272 20.99238995 21.99297718
 22.99356441 23.99415164 24.99473887 25.9953261  26.99591333 27.99650056
 28.99708779 29.99767502 30.99826225 31.99884948 32.99943671 34.00002394
 35.00061117 36.0011984  37.00178563 38.00237286 39.00296009 40.00354732
 41.00413455 42.00472178]
 
 
                             OLS Regression Results                            
===============================================================================
Dep. Variable:                       y   R-squared:                       0.999
Model:                             OLS   Adj. R-squared:                  0.999
Method:                  Least Squares   F-statistic:                 5.946e+04
Date:              sam., 08 févr. 2020   Prob (F-statistic):           1.56e-59
Time:                         15:43:41   Log-Likelihood:                -4.1622
No. Observations:                   38   AIC:                             12.32
Df Residuals:                       36   BIC:                             15.60
Df Model:                            1                                         
Covariance Type:             nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.9818      0.095     31.257      0.000       2.788       3.175
x1             2.0012      0.008    243.847      0.000       1.985       2.018
==============================================================================
Omnibus:                        4.839   Durbin-Watson:                   2.176
Prob(Omnibus):                  0.089   Jarque-Bera (JB):                1.959
Skew:                          -0.156   Prob(JB):                        0.375
Kurtosis:                       1.932   Cond. No.                         24.8
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Pour simplifier, on a une régression linéaire si :

  • R^2 (R-squared) est proche de 1.0

Mais il est toujours préférable de dessiner des données afin de vérifier qu'elles sont bien linéaires.

Les coefficiens doivent être pris en compte si P > |t| est proche de 0 et généralement inférieur à $0.05$.

On peut également regarder le coefficient Kurtosis qui représente une mesure de l'aplatissement des données mais pour une gaussienne. S'il est normalisé il est proche de 0, s'il est non normalisé il est proche de 3. Ici le coefficient est non normalisé, il est donc inférieur à 2 ce qui tendrait à dire que les données ne sont pas applaties or elles le sont.

Si le Kurtosis est non normalisé on considère que les données sont aplaties dans l'intervalle $[2,4]$ et non aplaties en dehors de cet intervalle.

Exercice 9.1

On considère les données du Quartet d'Anscombe.

Etablir pour chaque couple $(x_i,y_i)$ la régression linéaire simple et afficher les informations concernant la régression (OLS regression results).

  1. import numpy as np
  2.  
  3. matrix = np.array([
  4.   [10.0,  8.04, 10.0, 9.14, 10.0, 7.46, 8.0,  6.58],
  5.   [8.0, 6.95, 8.0,  8.14, 8.0,  6.77, 8.0,  5.76],
  6.   [13.0,  7.58, 13.0, 8.74, 13.0, 12.74,  8.0,  7.71],
  7.   [9.0, 8.81, 9.0,  8.77, 9.0,  7.11, 8.0,  8.84],
  8.   [11.0,  8.33, 11.0, 9.26, 11.0, 7.81, 8.0,  8.47],
  9.   [14.0,  9.96, 14.0, 8.10, 14.0, 8.84, 8.0,  7.04],
  10.   [6.0, 7.24, 6.0,  6.13, 6.0,  6.08, 8.0,  5.25],
  11.   [4.0, 4.26, 4.0,  3.10, 4.0,  5.39, 19.0, 12.50],
  12.   [12.0,  10.84,  12.0, 9.13, 12.0, 8.15, 8.0,  5.56],
  13.   [7.0, 4.82, 7.0,  7.26, 7.0,  6.42, 8.0,  7.91],
  14.   [5.0, 5.68, 5.0,  4.74, 5.0,  5.73, 8.0,  6.89]])
  15.  
  16.  

Etudier les paramètres suivants :

  • $R^2$
  • Prob (F-statistic)
  • Kurtosis
  • P > |t| pour les coefficients

9.3. Régression linéaire multiple en Python

9.3.1. Cas d'école

Etant donné un ensemble d'individus, connaissant leur nom, leur sexe, leur age, leur taille et leur poids, on se demande s'il est possible d'établir une relation linéaire qui permettrait de calculer le poids en fonction des autres données.

regression_lineaire_multiple.py

  1. #####################################################################
  2. # Exemple de régression linéaire multiple
  3. # étant donné un ensemble d'individus, connaissant leur nom,
  4. # leur sexe, leur age, leur taille et leur poids, on se demande
  5. # s'il est possible d'établir une relation linéaire qui permettrait
  6. # de calculer le poids en fonction des autres données
  7. #####################################################################
  8.  
  9.  
  10. #####################################################################
  11. # import des librairies
  12. #####################################################################
  13. from io import StringIO
  14. import numpy as np
  15. import pandas as pd
  16. import matplotlib.pyplot as plt
  17. import seaborn as sns
  18. from sklearn.linear_model import LinearRegression
  19. from sklearn.metrics import mean_squared_error, r2_score
  20. import statsmodels.api as sm
  21. import sys
  22. from mpl_toolkits.mplot3d import Axes3D
  23.  
  24. line = "=" * 50
  25. separator = "\n" * 2
  26.  
  27. #####################################################################
  28. # Données en entrée et en sortie
  29. #####################################################################
  30.  
  31. donnees = StringIO("""name,sex,age,size,weight
  32. "Joey", 1,  25,   72,   178
  33. "Jill", 0,  32,   68,   122
  34. "Jack", 1,  27,   69,   167
  35. "John", 1,  45,   67,   210
  36. "Jane", 0,  38,   62,   108""")
  37.  
  38. #
  39. # création d'un dataframe pandas
  40. # qui permet de manipuler facilement les données
  41. #
  42. df = pd.read_csv(donnees, sep=",")
  43.  
  44. print(line)
  45. print("Données initiales :")
  46. print(line)
  47. print( df.head() )
  48.  
  49. df = df.drop('name', axis=1)
  50.  
  51. #####################################################################
  52. # On sépare les données en deux catégories :
  53. # - les données ou rubriques (quantitatives et qualitatives) qui
  54. #   définissent un individu
  55. # - ce que l'on veut prédire, en l'occurrence, le poids
  56. #####################################################################
  57.  
  58. y = df.weight
  59.  
  60. # variables
  61. variables_du_modele = df.columns.drop(['weight'])
  62. X = df[ variables_du_modele ]
  63. #X = X.astype(float)
  64.  
  65. print(separator)
  66. print(line)
  67. print("Rubriques pour chaque individu :")
  68. print(line)
  69. print(X)
  70. print(line)
  71. print("Poids à prédire :")
  72. print(line)
  73. print(y)
  74.  
  75. #####################################################################
  76. # Matrice de corrélation
  77. #####################################################################
  78.  
  79. #
  80. # calcul de la matrice de corrélations
  81. #
  82. corr = X.corr()
  83.  
  84. #
  85. # dessiner la matrice avec ses valeurs (annot=True)
  86. #
  87. sns.heatmap(
  88.   corr,
  89.   cmap=sns.color_palette("YlOrRd", 10),
  90.   linewidths=.5,
  91.   annot=True,
  92.   xticklabels=corr.columns.values,
  93.   yticklabels=corr.columns.values
  94. )
  95. plt.title("Matrice de corrélation")
  96. plt.show()
  97.  
  98. #####################################################################
  99. # calcul de la régression
  100. #####################################################################
  101. modele = LinearRegression()
  102. modele.fit( X, y)
  103.  
  104. # affiche les coefficients
  105. print( "coefficients : ", modele.coef_ )
  106. print( "constante    : ", modele.intercept_ )
  107.  
  108. y_prime = modele.predict( X )
  109.  
  110. print(separator)
  111. print(line)
  112. print("Poids prédits : ", y_prime)
  113.  
  114. # Affiche l'erreur
  115. print('Erreur : %.2f' % mean_squared_error( y, y_prime) )
  116. # Affiche r^2
  117. print('r^2 %.2f' % r2_score(y, y_prime) )
  118.  
  119.  
  120. #####################################################################
  121. # Calcul des tests liés à la regression afin de valider le modèle
  122. #####################################################################
  123.  
  124. X_stats = sm.add_constant( X )
  125. stats = sm.OLS( y_prime, X_stats ).fit()
  126. print( stats.summary() )
  127.  
  128. #####################################################################
  129. # Affichage du résultat
  130. #####################################################################
  131.  
  132. fig = plt.figure()
  133. axes = fig.add_subplot(111, projection='3d')
  134. plt.title("Données avant régression")
  135. axe1 = X.age
  136. axe2 = X.size
  137. axes.scatter(axe1, axe2, y.astype(float).tolist(), c='green')
  138. axes.scatter(axe1, axe2, y_prime.astype(float).tolist(), c='red', marker='D', alpha=0.5)
  139. plt.show()
  140.  
  141.  
  142.  

9.3.2. Campagne de publicité

Nous allons considérer l'exemple advertising.csv qui est un fichier de données qui donne le millier d'unités vendues (Sales) pour un produit donné en fonction du budget marketing en milliers de dollars par le moyen de la télévision (TV), la Radio (radio) et des journaux (newspaper).

Premièrement, on charge le fichier .csv grâce à pandas et on récupère en retour un DataFrame qui est une classe pandas. On affiche ensuite les premières lignes du fichier.

  1. import pandas as pd
  2.  
  3. url = "http://www.info.univ-angers.fr/~richer/polytech/advertising.csv"
  4. df = pd.read_csv( url )
  5. print( df.head() )
  6. df = df.drop('Unnamed: 0', axis=1)
  7.  
  8.  

On s'aperçoit que la première colonne, appelée 'Unnamed: 0', n'a aucun intérêt pour la prédiction car elle représente un identifiant de ligne (variant de 1 à 200), il faut donc la supprimer grâce à la méthode drop du dataframe :


|<-- colonne DataFrame
|
   Unnamed: 0     TV  Radio  Newspaper  Sales
0           1  230.1   37.8       69.2   22.1
1           2   44.5   39.3       45.1   10.4
2           3   17.2   45.9       69.3    9.3
3           4  151.5   41.3       58.5   18.5
4           5  180.8   10.8       58.4   12.9

On trace ensuite un pair plot avec seaborn afin d'identifier des régressions linéaires potentielles :

  1. import seaborn as sns
  2. import matplotlib.pyplot as plt
  3.  
  4. graphe = sns.pairplot(df)
  5. plt.show()
  6.  
  7.  

Exercice 9.2

Y a t-il des régressions linéaires entre deux variables sur le graphe obtenu ?

La matrice de corrélation permet également d'identifier des relations :

  1. corr = df.corr()
  2. sns.heatmap(corr, cmap=sns.color_palette("YlOrRd", 10),
  3.   linewidths=.5,
  4.   annot=True,
  5.   xticklabels=corr.columns.values,
  6.   yticklabels=corr.columns.values)
  7. plt.show()
  8.  
  9.  

On tente d'établir une régression linéaire multiple de manière à savoir si les campagnes marketing (TV, Radio, Journaux) ont une influence sur le résultat des ventes :

$$ Sales = constante + a_1 × TV + a_2 × Radio + a_3 × Newspaper $$
  1. from sklearn.linear_model import LinearRegression
  2.  
  3. # instance de la classe LinearRegression
  4. modele = LinearRegression()
  5.  
  6. # variables
  7. variables_du_modele = df.columns.drop(['Sales'])
  8.  
  9. # y est le vecteur de sortie à prédire
  10. y = df.Sales
  11. # X est une matrice des données en entrées
  12. X = df[ variables_du_modele ]
  13.  
  14. # on appelle la méthode fit() qui réalise les calculs de la
  15. # régression linéaire multiple
  16. modele.fit( X, y)
  17.  
  18.  

Dès lors, on peut afficher les coefficients de la relation :

  1. separator = "\n" * 2
  2.  
  3. print(separator)
  4. print("Sales = %.4f" % modele.intercept_, end='')
  5. for col_index, col_name in enumerate(modele.coef_):
  6.   print( ' + %.4f' % modele.coef_[col_index], ' * ', df.columns[col_index], end='')
  7. print()
  8. print(separator)
  9.  
  10.  

Il faut ensuite déterminer quelles variables sont pertinentes pour la relation.

  1. import statsmodels.api as sm
  2.  
  3. X_stats = sm.add_constant( X )
  4. stats = sm.OLS( y, X_stats ).fit()
  5. print( stats.summary() )
  6.  
  7.  

Le meilleur moyen est d'utiliser la p-value qui permet ou non de rejeter l'hypothèse nulle, c'est à dire le fait qu'il n'y a pas de relation de corrélation entre une variable des caractéristiques et la variable à prédire.

Si la p-value est inférieure à 0.05 alors la variable est corrélée à la variable à prédire.

===============================================================================
Dep. Variable:                   Sales   R-squared:                       0.897
Model:                             OLS   Adj. R-squared:                  0.896
Method:                  Least Squares   F-statistic:                     570.3
Date:              jeu., 06 févr. 2020   Prob (F-statistic):           1.58e-96
Time:                         18:22:19   Log-Likelihood:                -386.18
No. Observations:                  200   AIC:                             780.4
Df Residuals:                      196   BIC:                             793.6
Df Model:                            3                                         
Covariance Type:             nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const          2.9389      0.312      9.422      0.000       2.324       3.554
TV             0.0458      0.001     32.809      0.000       0.043       0.049
Radio          0.1885      0.009     21.893      0.000       0.172       0.206
Newspaper     -0.0010      0.006     -0.177      0.860      -0.013       0.011
==============================================================================
Omnibus:                       60.414   Durbin-Watson:                   2.084
Prob(Omnibus):                  0.000   Jarque-Bera (JB):              151.241
Skew:                          -1.327   Prob(JB):                     1.44e-33
Kurtosis:                       6.332   Cond. No.                         454.
==============================================================================

On voit donc qu'a priori les journaux (newspaper) n'ont pas d'influence sur la relation linéaire.

Exercice 9.3

Afficher sous forme de graphique 3D la propriété à prédire et celle prédite en fonction de TV et Radio. Que remarque t-on ?

Exercice 9.4

Quels résultats (combien d'unités seront vendues) avec les budgets suivants :

  • [57.0, 32.0, 23.0] (TV, Radio, Newspaper)
  • [23.0, 32.0, 78.0] (TV, Radio, Newspaper)

Que peut-on dire de ces résultats, sont-ils valides ?

Exercice 9.5

On s'intéresse à la durée de la période de gestation de femmes ayant fumé ou pas pendant leur grossesse.

On dispose d'un fichier de 32 femmes et leurs enfants pour lesquels on a les données suivantes :

  • Wgt : poids en grammes du bébé à la naissance
  • Gest : durée de la période de gestation en semaines
  • Smoke : le fait que la maman ait fumé (yes) ou non (no)

Dessiner un graphique avec la période de gestation en fonction des fumeuses ou non fumeuses.

Note : les données sont disponibles ici.