Cette page fait partie du cours de polytech PeiP1 et 2 Bio
6. Mise en pratique : N-reines
6.1. Introduction
Le problème des N-reines consiste à placer sur un échiquier de $NxN$ cases, $N$ reines de manière à ce qu'aucune reine ne soit en prise avec une autre.
Ce problème a été posé en 1848 par un joueur d'échecs allemand, Max Bezzel, pour $N = 8$.
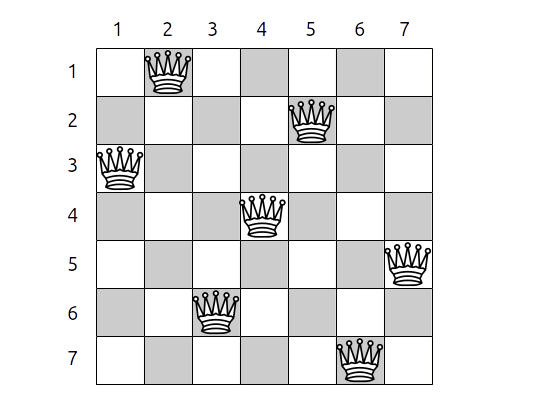
Solution pour N=7
Voici le nombre solutions en fonction de $N$ :
| N | Solutions |
| 2 | 0 |
| 3 | 0 |
| 4 | 2 |
| 5 | 10 |
| 6 | 4 |
| 7 | 40 |
| 8 | 92 |
| 9 | 352 |
| 10 | 724 |
| 11 | 2680 |
| 12 | 14200 |
Exercice 6.1
Quelle est la complexité de la résolution de ce problème ?
6.2. Résolution
Nous allons étudier plusieurs algorithmes de résolution du problème, à savoir :
- méthode 1 : utilisation des permutations
- méthode 2 :utilisation d'un échiquier et vérification des prises (récursif avec retour arrière)
- méthode 3 :utilisation remplissage des cases en prises de l'échiquier (récursif avec retour arrière)
- méthode 4 :utilisation de tableaux qui modélise les colonnes et diagonales (récursif avec retour arrière)
6.2.1. Méthode des permutations
Une première méthode issue du livre Python 3, les Fondamentaux du langage, Sébastien Chazallet, Editions ENI (page 428), utilise les permutations et vérifie que deux reines ne sont pas en prise en comparant le nombre d'éléments dans chaque ensemble de diagonales.
La méthode est concise et intéressante d'un point de vue intellectuel mais totalement inefficace car il faut tester chaque permutation, soit $N!$. Pour s'en convaincre, on consultera la section Résultats
- from itertools import permutations
- import time
- nbr_permutations = 0
- # méthode de résolution
- # basée sur les permutations
- def resoudre(n):
- global nbr_permutations
- columns = range(n)
- for board in permutations(columns):
- nbr_permutations = nbr_permutations + 1
- s1 = set(board[i] + i for i in columns)
- s2 = set(board[i] - i for i in columns)
- if n == len(set(board[i] + i for i in columns)) == len(set(board[i] - i for i in columns)):
- yield board
- # nombre de reines
- N = 6
- t1 = time.time()
- ns = len(list(resoudre(N)))
- t2 = time.time()
- print("reines=", N)
- print("permutations=", nbr_permutations)
- print("solutions=", ns)
- print("temps de calcul=", t2-t1)
6.2.2. Méthode des prises sur l'échiquier
Le principe est simple : on modélise l'échiquier sous forme d'une matrice de $N$ par $N$ entiers.
- initialiement la matrice est composée de 0
- placer une reine sur l'échiquier consiste à assigner à la case correspondante la valeur de la reine (variant de 1 à $N$)
- on commence par la reine en ordonnée 1, puis 2, etc
- à chaque étape on vérifie qu'il n'y a pas de prise :
- avec une reine située sur une ordonnée inférieure
- avec une diagonale positive supérieure
- avec une diagonale négative supérieure
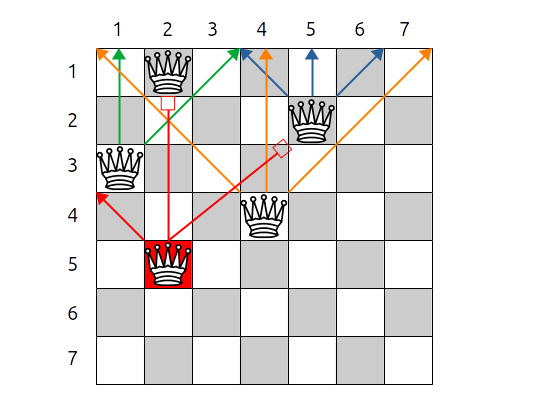
Sur la figure précédente, la reine en ligne 5, colonne 2 est en prise avec deux autres reines.
Exercice 6.2
Implantez la résolution en utilisant la méthode par vérification des prises.
On utilisera une matrice de type numpy de N+1 par N+1 éléments entiers et on utilisera uniquement les cases d'indice 1 à N
import numpy as np
N = ...
echiquier = np.zeros((N+1)*(N+1), dtype=int).reshape(N+1, N+1)
6.2.3. Méthode de remplissage des prises de l'échiquier
Dès qu'on place une reine, on affecte les cases de l'échiquier concernées par une prise de manière à indiquer quelles cases sont inutilisables par la suite pour le positionnement des reines suivantes.
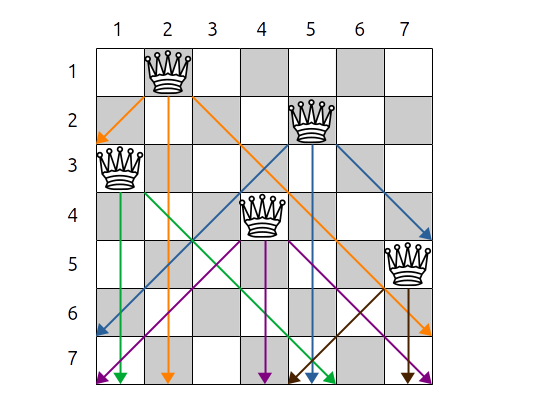
Exercice 6.3
Implantez la résolution en utilisant la méthode par remplissage des prises.
6.2.4. Méthode des tableaux colonnes et diagonales
Au lieu d'utiliser un échiquier de $N$ par $N$ cases, on utilise trois tableaux d'entiers :
- un tableau de $N+1$ cases qui représente les colonnes
- un tableau de $2N+1$ cases qui représentent les diagonales positives occupées
- un tableau de $2N+1$ cases qui représentent les diagonales négatives occupées
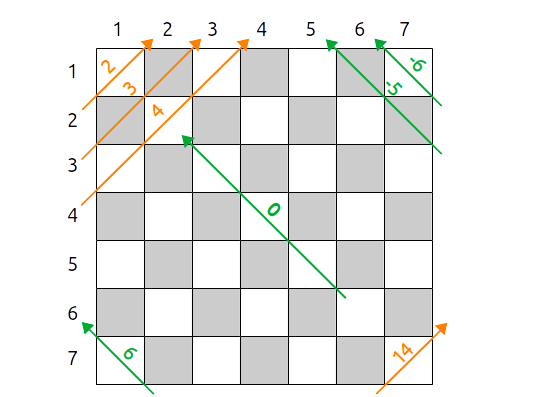
Diagonales positive (orange) et négatives (vert)
Ces tableaux sont initialisés avec des 0. Dés qu'on place une reine $r$ dans la colonne $c$, on positionne à $r$ la colonne et la diagonale correspondante :
- colonnes$[c]=r$
- diagonale_positive$[c+r]=r$
- diagonale_negative$[r-c+N]=r$
Exercice 6.4
Implantez la résolution en utilisant la méthode par tableaux colonnes et diagonales.
6.3. Résultats
Voici un tableau comparatif des temps d'exécution des méthodes pour la résolution du problème des N-reines pour $N=12$ :
| Méthode | i7-4790 @ 3.60GHz |
Ryzen 1700X 3.4 Ghz |
| méthode 1 (permutations) | (29m40s) 1780 | (33m56s) 2036 |
| méthode 2 (prises échiquier) | 33,4 | 50,1 |
| méthode 3 (remplissage échiquier) | 15,3 | 22,2 |
| méthode 4 (tableaux) | 3,7 | 6,0 |
| méthode 4 (en C++) | 0,5 | 0,6 |
Remarque : la méthode 3 est utilisée avec une matrice Numpy d'entiers. Si on implante la solution en utilisant un tableau de tableaux d'ensembles, on va beaucoup plus vite (9s au lieu de 15s).
Dans ce cas on crée l'échiquier sous la forme :
echiquier = [ [set() for x in range(0,N+1)] for y in range(0,N+1) ]
Exercice 6.5
Réalisez des tests de performance pour $N=10$ afin de comparer les quatre méthodes de résolution.