Cette page fait partie du cours de polytech PeiP1 et 2 Bio
4. Mise en pratique : Problème du Cavalier
4.1. Introduction
Certains traitements peuvent être définis sous forme de relation de récurrence. Par exemple les suites sont un exemple idiomatique de la récurrence :
La suite de Syracuse est définie comme suit :
- on part d'un nombre entier plus grand que zéro $x$
- s'il est pair, on le divise par 2
- s'il est impair, on le multiplie par 3 et on ajoute 1
Exercice 4.1
Ecrire un programme Python nommé syracuse.py qui, étant donné un nombre $x$ passé en paramètre à une fonction du même nom, permet de calculer et d'afficher les 100 premiers nombres de la suite de Syracuse qui lui est associée. Par exemple pour 19, on obtient :
[19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4]
4.2. Récursion et condition d'arrêt
On peut calculer une relation de récurrence mais si elle ne termine jamais on est confronté à un problème.
En informatique la récurrence est mise en oeuvre au travers de la récursivité. On parle de récursivité lorsqu'une fonction s'appelle ou lorsqu'une structure de données s'auto-référence.
Une fonction récursive doit comporter deux choses :
- une relation de récurrence
- une condition d'arrêt de la récurrence
Prenons l'exemple de la fonction factorielle : $n! = n × n-1 × … × 2 × 1$.
Ici la relation de récurrence est simple. Si on appelle $f(n) = n!$ alors :
- la relation de récurrence est $f(n) = n × f(n-1)$
- la condition d'arrêt est $n = 1$.
L'implantation en Python est triviale :
- def factorielle(n):
- if n == 1:
- return 1
- else:
- return n * factorielle(n-1)
- for i in range(1, 11):
- print(i, factorielle(i))
Exercice 4.2
A titre d'exercice écrire un programme Python nommé fibonacci.py qui affiche les 20 premiers termes de la suite de fibonacci implantée sous forme d'une fonction récursive :
- $fibonacci(0) = 0$
- $fibonacci(1) = 1$
- $fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)$
Exercice 4.3
Reprendre la suite de syracuse et écrire un programme qui utilise une fonction récursive syracuse_recursive() et qui calcule les 100 premiers termes de la suite pour $x=200$ et affiche cette liste. On doit obtenir :
[200, 100, 50, 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4]4.3. Le problème du cavalier
Etant donné un échiquier de $n × n$ cases, un cavalier étant placé sur la première case en haut à gauche (ou sur n'importe quelle autre case), peut on déplacer le cavalier de manière à ce qu'il passe une seule fois par toutes les cases ?
Le problème du cavalier est un cas particulier des graphes hamiltoniens dans la théorie des graphes. Un chemin hamiltonien d'un graphe orienté est un chemin qui passe par tous les sommets une fois et une seule.
On pourra consulter Wikipédia pour plus d'informations.
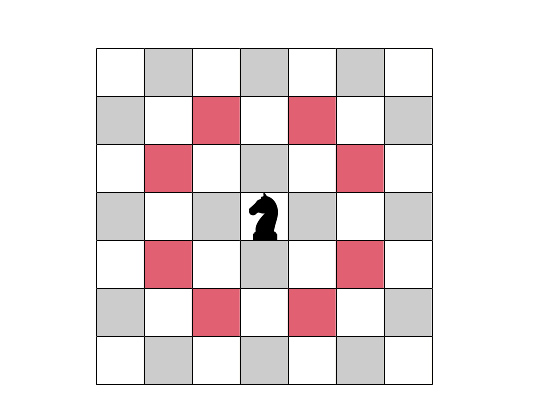
Exemple des 8 déplacements possibles du cavalier
Il s'agit d'un problème combinatoire qui demande beaucoup de calculs car il faut tester tous les cas possibles pour trouver toutes les solutions. Ce problème est en effet NP-Complet.
4.4. Résolution
4.4.1. Définition des variables
On commence par définir les variables dont on aura besoin :
- // dimension de l'échiquier
- dimension est un entier = 5
- // définition de l'aire de jeu
- échiquier est une matrice d' entiers [dimension, dimension]
- // nombre de solutions trouvées
- nbr_solutions est un entier = 0
- // déplacements du cavalier sur l'axe des x
- d_x est un tableau d' entiers = [-1, 1, 2, 2, 1, -1, -2, -2]
- // déplacements du cavalier sur l'axe des y
- d_y est un tableau d' entiers = [-2, -2, 1, -1, 2, 2, -1, 1]
Initialement chaque case de l'échiquier contiendra la valeur 0 pour indiquer qu'elle n'a pas encore été visitée. Puis au fur et à mesure de la recherche l'échiquier se remplit avec des valeurs positives : 1 représente la première case visitée, puis 2 la seconde, etc.
4.4.2. Algorithme de résolution
On conçoit ensuite l'algorithme de résolution du problème qui est un sous-programme récursif basé sur le retour-arrière (backtrack).
| Procédure résoudre(y, x, étape) | |
|---|---|
| Entrée |
y position en y sur le damier x position en x sur le damier étape nième itération |
| Sortie | on ne retourne aucune valeur mais on augmente le nombre de solutions trouvées |
| Variables globales |
|
| Variables locales |
(y_s, x_s) : prochaine position du cavalier |
| Description | On cherche de manière récursive toutes les solutions en essayant toutes les positions possibles du cavalier (x_s, y_s). Si le cavalier est à l'intérieur de l'échiquier on continue la recherche |
|
|
Enfin, la résolution du problème s'effectue en appelant le sous-programme de résolution en partant de la position (1,1) -- en haut à gauche, soit (0,0) en Python -- et en considérant qu'il s'agit de l'étape 1.
Exercice 4.4
Ecrire un programme Python nommé cavalier.py qui résoud ce problème.
- on commence par créer l'échiquier composé de $n × n$ cases initialisées à 0
- on écrit ensuite la fonction récursive resoudre(y,x,etape)
- on appelera la fonction sous la forme suivante resoudre(0,0,1) pour résoudre le problème en plaçant le cavalier sur la première ligne et en première colonne
4.5. Résultats
Avec Python le temps de résolution est prohibitif, pour $n=6$ après 7 heures de calcul on a obtenu 167_610 solutions sur les 524_486 existantes.
| n | C++ | Python | Amélioration | Solutions |
| 5 | 0,31 | 11,34 | 36,58 | 304 |
| 6 | 250 | >7h (167610) | ? | 524486 |
Dans la table précédente on a indiqué (colonne Amélioration) le facteur d'amélioration entre C++ et Python (càd le rapport temps_C++ / temps_Python).