5. Jeu de la vie

On s'intéresse à la parallèlisation de l'algorithme du jeu de la vie.

Récupérer l'archive jeu_de_la_vie.tgz et paralléliser le code. Comparer les temps d'exécution des différentes méthodes :

• méthode 1 : sans parallélisation, mono thread (gol_cpu.exe)
• méthode 2 : en utilisant OpenMP sur la première boucle de la fonction kernel (écrire gol_cpu_omp.cpp et générer gol_cpu_omp.exe)
• méthode 3 : en utilisant OpenMP sur les deux boucles de la fonction kernel en utilisant collapse (écrire gol_cpu_omp_collapse.cpp et générer gol_cpu_omp_collapse.exe)
• méthode 4 : en utilisant MPI lors de l'utilisation de la fonction kernel (écrire gol_cpu_mpi.cpp et générer gol_cpu_mpi.exe)

On effectuera les tests avec les paramètres -t -s 2048 -m 10000, c'est à dire

• -t : un test de performance
• -s 2048 : une aire de jeu de 2048x2048 cases
• -m 10000 : pour 10000 générations

On pourra éventuellement modifier le paramètre -m si le nombre de générations donne des temps de calcul trop importants

5.1. L'implantation mono thread

Elle se base sur l'utilisation d'un tableau à une dimension de $(n+2) × (n+2)$ octets, si $n$ est la taille de l'aire de jeu. En effet, on mettra les lignes qui correspondent aux bords à 0 et elle ne seront jamais modifiées. Cela permet de simplifier les calculs. Une cellule prend donc deux valeurs : 1 (vivante), 0 (morte).

Pour le calcul de la génération suivante, pour chaque cellule ($x, y ∈ [1,n]$), on doit compter le nombre de cellules vivantes autour de la cellule en coordonnées $(x,y)$. Il faut regarder la fonction nommée kernel() dans le fichier gol_cpu.cpp

La cellule sera vivante dans la prochaine génération, si :

• elle est déjà vivante et qu'elle possède deux voisins vivants
• ou si elle est morte et possède trois voisins vivants

5.2. Parallélisation avec OpenMP

On pensera à paralléliser la boucle principale du calcul et éventuellement les deux boucles en utilisant l'option collapse(2).

Donner un tableau du temps de calcul pour $k=1, 2, 4, 6, 8, 10, 12, ..., 32$ threads de calcul. Que remarquez vous sur votre processeur ? Pour quel nombre de threads le temps est-il minimal ?

On enregistrera les temps de calcul dans un fichier en utilisant la commande /usr/bin/time -f "%U %e" ./gol_cpu_omp.exe ...

Voici un exemple de fichier résultat avec 3 champs (sur un AMD Ryzen 5 3600 pour la parallélisation de la première boucle $y$) :

• le premier champ représente le nombre de threads utilisés ($k$)
• le second champ est le temps cumulé $T = k × T_e$
• le troisième champ est le temps écoulé ($T_e$, elapsed) qui correspond au temps d'exécution en parallèle

1 22.07 22.11
2 21.48 10.76
4 22.09 5.55
6 22.88 3.84
8 36.05 4.53
10 36.47 3.67
12 37.48 3.16
14 34.69 4.58
16 34.00 4.53
18 34.10 4.65
20 34.74 5.01
22 34.89 5.23
24 35.24 5.59
26 35.28 5.89
28 35.67 5.94
30 36.10 6.01
32 36.53 6.09

Par exemple pour $k = 12$, le temps d'exécution (réel) est de $3.27$ secondes, soit un temps cumulé de $12 × 3.27 = 39.24$. Or, on nous indique un temps cumulé de $38.62$, donc inférieur, ce qui implique que certains threads ont probablement mis moins de $3.27$ secondes pour s'exécuter.

Voici, sous forme graphique, grâce à gnuplot, une visualisation des résultats précédents avec parallélisation de la première boucle.

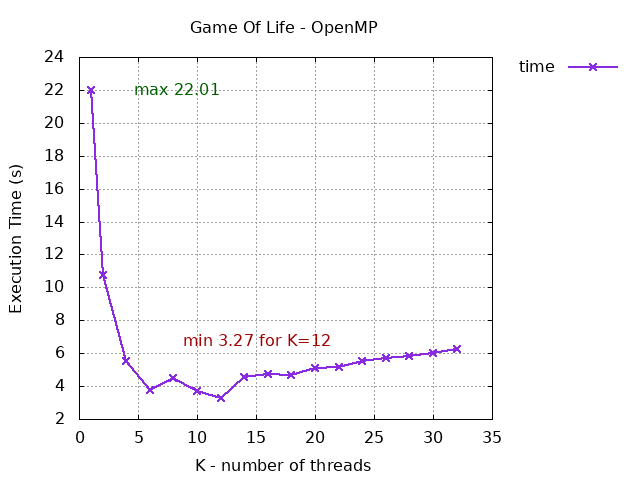
!!! Attention !!! Il est préférable de lancer les tests sans autre programme tournant en tâche de fond comme un navigateur afin d'obtenir les résultats les plus précis possibles.

5.3. Parallélisation avec MPI

La partie MPI est plus complexe à mettre en oeuvre. On peut utiliser autant de processus de calcul que l'on désire et c'est la fonction kernel() qu'il faut modifier comme précédemment :

• dans un premier temps, il faut calculer les lignes que chaque processus devra traiter; par exemple pour $n=2048$ et $k=6$, on doit avoir :

  
  # nombre de lignes par processus
  k=0: 342
  k=1: 342
  k=2: 341
  k=3: 341
  k=4: 341
  k=5: 341
  
  # ligne de début et ligne de fin
  k=0:    1 ->  342
  k=1:  343 ->  684
  k=2:  685 -> 1025
  k=3: 1026 -> 1366
  k=4: 1367 -> 1707
  k=5: 1708 -> 2048
  
  

• dans un second temps, on modifie la boucle des générations :
  • le maître envoie aux esclaves le tableau de cellules en entrée : par exemple si on a utilisé -s 2048, cela signifie que les tableaux alloués sont de taille 2050x2050, on doit donc transmettre un tableau de 4202500 octets à chaque esclave
  • chaque processus esclave (ainsi que le maître) traite les lignes qu'il a à traiter
  • les esclaves renvoient leur résultat (les lignes qu'ils ont traitées) au maître.

Dans une première implantation, on peut utiliser send et receive et faire en sorte que le maître envoie l'aire de jeu complète (2050x2050) aux esclaves.

Dans une seconde implantation, on peut faire en sorte que le maître envoie uniquement aux esclaves les lignes qu'ils doivent traiter (Par exemple, pour l'exemple précédent, pour $k=6$, il faudra que le maître envoie au processus esclave $2$, les lignes 684 à 1026).

5.4. Résultats

Sur un AMD Ryzen 5 3600 qui est un hexacore + SMT, on obtient les résultats suivants :

###############################################################
 MONO THREAD
###############################################################
1 22.29 22.31
---------------------------------------------------------------
###############################################################
 MULTI THREAD OPENMP
###############################################################
1 21.96 22.01
2 21.48 10.76
4 22.06 5.54
6 22.51 3.78
8 35.87 4.51
10 36.50 3.68
12 38.62 3.27
14 34.42 4.58
16 33.57 4.75
18 34.05 4.68
20 34.43 5.09
22 34.71 5.15
24 35.06 5.50
26 35.23 5.73
28 35.59 5.84
30 35.98 5.99
32 36.81 6.23
---------------------------------------------------------------
###############################################################
 MULTI THREAD OPENMP COLLAPSE
###############################################################
1 143.41 143.48
2 146.52 73.40
4 149.87 37.58
6 158.57 26.53   !!!
8 268.15 33.64
10 276.83 27.83
12 326.41 28.51
14 248.58 32.75
16 246.19 31.54
18 244.39 31.71
20 247.03 30.91
22 248.90 30.91
24 249.28 30.97
26 249.46 30.59
28 249.68 31.02
30 248.61 31.20
32 250.57 30.06
---------------------------------------------------------------
###############################################################
 MULTI THREAD - MPI version 1 
###############################################################
2 31.22 19.38
3 49.92 21.46
4 83.66 26.38
5 121.05 29.40
6 185.26 36.48   !!!
###############################################################
 MULTI THREAD - MPI version 2
###############################################################
2 29.56 18.43
3 36.75 14.89
4 46.65 13.83
5 59.57 14.01
6 68.60 13.27
---------------------------------------------------------------

• Le temps en mono thread est d'environ 22 secondes.
• Avec OpenMP et parallélisation de la première boucle, on doit normalement obtenir un temps minimal pour le nombre de threads du processeur, en l'occurrence ici, pour 12 threads on a 3,27 s.
• Avec OpenMP et parallélisation avec collapse, les temps de calcul sont anormalement élevés, et même plus élevés qu'en mono thread. Cela vient probablement d'un bug d'OpenMP ou alors de la manière dont sont accédées les données.
• Avec MPI, dans le cas de la première implantation, le temps de calcul augmente en fonction du nombre de processus utilisés cela est probablement dû au trop grand nombre de données qui sont échangées entre processus.
• La version 2 de MPI qui se limite à envoyer les lignes nécessaires et non toute l'aire de jeu, permet d'obtenir un gain important par rapport à la première version mais on reste moins performant que pour OpenMP.