IA et Jeux
Méthodes de Résolution
Ce chapitre est une courte introduction aux jeux et aux principes de résolution de ces jeux avec IA.
1.1. Jeu de Nim
Le Jeu de Nim est un jeu à deux joueurs qui consiste, étant données $n$ allumettes, à prendre à tour de rôle 1, 2 ou 3 allumettes. Le perdant est le joueur qui prend la dernière allumette.
Il s'agit d'un jeu dit à somme nulle, c'est à dire que la somme des gains et des pertes de tous les joueurs est égale à 0. Dans le cas présent il y a un gagnant et un perdant.
Par opposition on parle de jeu à somme non nulle tel le le dilemme du prisonnier.
Examinons une situation de jeu pour 4 allumettes :
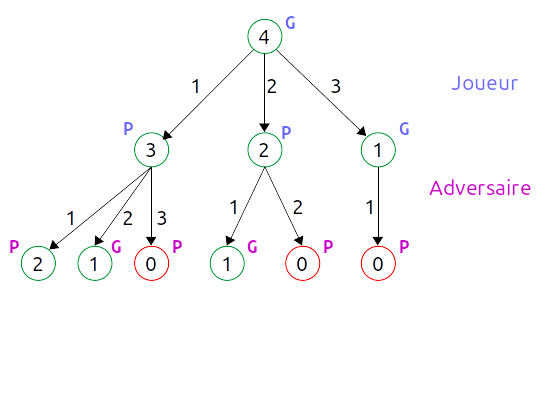
Pour 4 allumettes :
- si j'en prends 3, alors je gagne car il ne reste qu'une seule allumette et mon adversaire est contraint de la prendre
- si j'en prends 2, alors je perds car si mon adversaire en prend une seule, alors je serai contraint de prendre la dernière allumette
- si j'en prends 1, alors je perds car si mon adversaire en prend deux, alors je serai contraint de prendre la dernière allumette
| Allumettes restantes |
Allumette(s) prise(s) |
Situation |
| 1 | 1 | P |
| 2 | 1 | G |
| 3 | 2 | G |
| 4 | 3 | G |
| 5 | 1,2,3 | P |
| 6 | 1 | G - situation 5 pour adversaire |
| 6 | 2 | P - situation 4 pour adversaire |
| 6 | 3 | P - situation pour adversaire |
Au final, si $n = 4p + 1$ alors on perd.
Il s'agit donc d'un jeu qui ne demande aucune IA pour gagner il suffit d'appliquer la formule et faire en sorte que l'adversaire soit dans une situation ou $n = 4p + 1$
1.2. Jeu états / transitions
Les jeux comme missionnaires et cannibales, chèvre, choux, loup (passage de rivière font partie des jeux états / transitions.
Considérons le jeu des bouteilles : on dispose de 2 bouteilles puvant contenir 4 et 3 litres respectivement. Comment faire pour obtenir une bouteille qui contienne exactement 2 litres ? Eventuellement on peut se demander qu'elle est la solution qui demande le moins d'étapes.
On définit donc pour ce jeu :
- un état initial $(0,0)$ pour lequel la grande bouteille $G$ de 4 litres et la petite bouteille $P$ de 3 litres sont vides
- un ou des états finaux : $(0,2)$, $(2,0)$, $(2,2)$
On définit ensuite les transitions :
- remplir $G$ : $(x,y) → (4,y)$, si $x < 4$
- remplir $P$ : $(x,y) → (x,3)$, si $y < 3$
- vider $G$ : $(x,y) → (0,y)$, si $x > 0$
- vider $P$ : $(x,y) → (x,0)$, si $y > 0$
- verser $G$ dans $P$ :
- $(4,0) → (1,3)$
- $(4,1) → (2,3)$
- $…$
- verser $P$ dans $G$ :
- $(0,3) → (3,0)$
- $(1,3) → (4,0)$
- $…$
Pour résoudre le problème il suffit de partir de l'état initial pour arriver sur l'un des états finaux, on peut pour cela envisager plusieurs stratégies :
- génération en profondeur d'abord (depth first)
- génération en largeur d'abord (breadth first)
Discutez des avantages et inconvénients de ces stratégies.
// génération en largeur d'abord
pile = { etat_initial }
tant que pile.non_vide() faire
etat = pile.depiler()
si etat = etat_final alors
print "Solution !"
sortir du tant que
sinon
pour toute transition (e_i, e_f) telle que e_i = etat faire
pile.empiler(e_f)
fin pour
fin si
fin tant que
Exercice 1.1
Programmer ce jeu et trouver la solution la plus courte partant de $(0,0)$ pour arriver à l'état final $(2,0)$.
1.3. Jeu avec IA de type MIN/MAX
Considérons le jeu de l'Awalé, jeu africain, qui consiste à partir d'un plateau de jeu sur lequel on a placé des billes, à récupérer le plus de billes possibles. On donne ici des règles de jeu simplifiées.
Chaque joueur dispose de 6 cases, dans lesquelles on trouve initialement 4 billes, et d'un grenier dans lequel il place les billes gagnées.
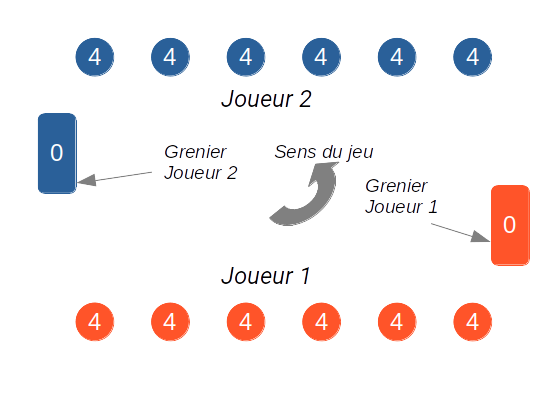
Lorsqu'un joueur joue, il prend les billes dans une de ses cases et les égraine dans le sens inverse des aiguilles d'une montre. S'il passe par son grenier, il dépose une bille mais il ne dépose jamais de bille lorsqu'il passe par le grenier de son adversaire.
Si le joueur termine sur l'une de ses cases, il prend les billes en regard chez son adversaire et les place dans son grenier :
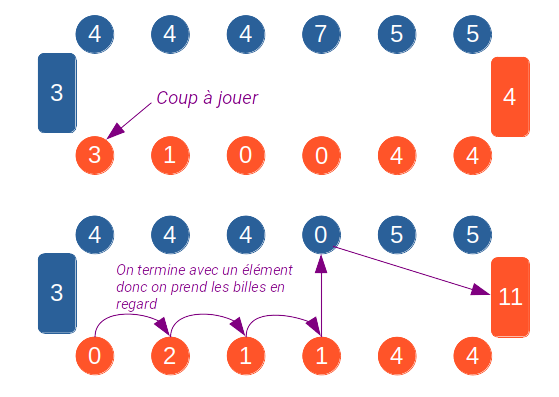
1.3.1. IA min/max
Afin de pouvoir faire jouer une IA, on définit pour ce type de jeu, une fonction d'évaluation $f$ qui aura pour but de donner une valeur d'autant plus grande que la situation de jeu mène à une situation gagnante et d'autant plus faible qu'elle mène à une situation perdante.
La fonction la plus simple est la différence entre les billes du grenier du joueur et celles dans le grenier de son adversaire. En effet :
- si $f$ est positive alors c'est le joueur qui est dans une situation gagnante
- si $f$ est négative alors c'est son adversaire qui est dans une situation gagnante
On parle d'algorithme de type min/max car :
- pour le joueur, on tente de maximiser $f$, donc on maximise ses gains
- alors que pour l'adversaire, on tente de minimiser $f$, donc on minimise les gains de l'adversaire
La technique consiste à génèrer un arbre des coups jouables jusqu'à un certain niveau, puis à évaluer la situation de jeu au niveau le plus profond et faire remonter cette situation à la racine de l'arbre afin de savoir quel coup jouer.
1.3.1.a Jouer sur un niveau de profondeur
Partons de la situation initiale suivante pour le joueur 1 (en bleu) :
0 3 2 0 0 0 21 19 1 0 0 0 2 0
S0
qui donne lieu aux deux situations de jeu suivantes :
| niveau 0 | niveau 1 | |
0 3 2 0 0 0 21 19 1 0 0 0 2 0 |
max(+1, -1) = +1 | 0 0 2 0 0 0 21 22 0 1 0 0 2 0 |
0 3 2 0 0 0 21 20 1 0 0 0 0 1 |
Nous avons indiqué en bleu le score (ou coût) de la fonction $f$ pour le joueur 1. Initialement au niveau 0, le score de $f$ est de -2 ($19 - 21$) pour le joueur 1, ce qui signifie que le joueur 1 possède un déficit de deux billes.
Sur les deux situations de jeu qui découlent de la situation initiale, l'une permet au joueur 1 de faire mieux que son adversaire puisqu'on arrive à un score de +1. Le joueur doit donc jouer la case 1 à partir de la situation initiale (S0).
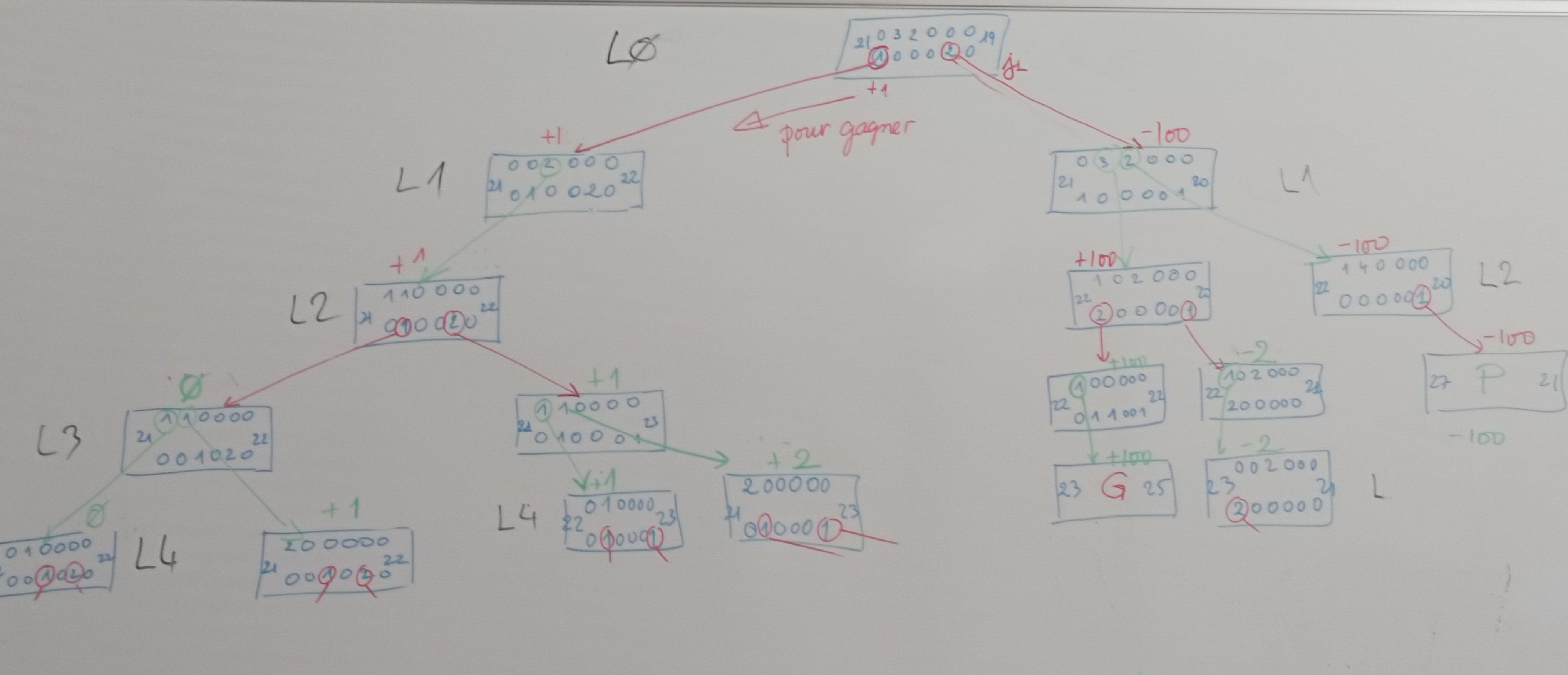
1.3.1.b Jouer sur deux niveaux de profondeur
On va à présent jouer sur deux niveaux afin d'obtenir plus d'informations :
- au niveau 0, c'est la situation de départ, on prendra le maximum des valeurs obtenues au niveau 1, ce qui nous donnera le coup à jouer
- au niveau 1, on récupère les valeurs de l'adversaire, on choisira donc le minimum des valeurs obtenues
- au niveau 2, c'est l'adversaire qui joue et on retournera les valeurs de $f$
| niveau 0 | niveau 1 | niveau 2 | ||
0 3 2 0 0 0 21 19 1 0 0 0 2 0 |
max(+1, -2) = +1 | 0 0 2 0 0 0 21 22 0 1 0 0 2 0 |
min( +1 ) = +1 | 1 1 0 0 0 0 21 22 0 1 0 0 2 0 |
0 3 2 0 0 0 21 20 1 0 0 0 0 1 |
min(-2, -2) = -2 | 1 4 0 0 0 0 22 20 0 0 0 0 0 1 |
||
1 0 2 0 0 0 22 20 2 0 0 0 0 1 |
Les données remontées au niveau de la racine nous indiquent :
- qu'il faut jouer la situation S1, c'est la situation la plus favorable pour nous puisqu'on a une bille de plus que notre adversaire.
- que la situation S5 nous amène à perdre 2 billes.
1.3.1.c Jouer sur quatre niveaux de profondeur
Sur quatre niveaux de profondeur, on obtient la figure suivante :
- la situation S1 est toujours la même et nous amène à avoir une bille de plus que notre adversaire
- par contre la situation S5 nous amène à une situation gagnante (+100) et une situation perdante (-100), et dans ce cas, c'est la situation perdante qui sera remontée, on ne doit donc pas jouer S5; en effet, même s'il est possible pour nous de gagner, notre adversaire possède la possibilité de gagner également et on imagine bien qu'il ne s'en privera pas
1.3.1.d Jouer sur huit niveaux de profondeur
Sur huit niveaux de profondeur, on obtient la figure suivante et on dispose encore de plus d'information :
- la situation S1 nous amène uniquement à des situations gagnantes
- la situation S5 nous amène à deux situations gagnantes (+100) et une situation perdante (-100), il ne faut donc surtout pas jouer S5 comme indiqué précédemment
1.3.1.e Algorithme et analyse du min/max
L'algorithme du min/max peut se résumer comme ci-après. La plupart des algorithmes donnés sur internet ou dans des ouvrages d'IA sont généralement très mal conçus et donc pas implantables pour permettre de fournir une IA capable de gagner.
Généralement on ne définit qu'une seule fonction mais je préfère la séparer en trois fonctions distinctes :
- max_min( jeu, joueur ), la fonction principale qui retourne le coup à jouer; on appelle cette fonction max_min (et non min_max) car on cherche à maximiser le gain du joueur que l'on passe en paramètre de la fonction
- min( jeu, joueur, adversaire, profondeur ), fonction utilisée quand c'est l'adversaire du joueur à faire gagner qui joue, on tente alors de minimiser le gain de l'adversaire
- max( jeu, joueur, adversaire, profondeur ), fonction utilisée quand c'est au joueur que l'on tente de faire gagner de jouer
En fonction de la profondeur maximale, la fonction max_min commence par appeler la fonction min qui appellera la fonction max qui, à son tour, appellera la fonction min, etc.
Lorsque l'on a atteint la profondeur maximale ou que l'on ne peut plus jouer, on retourne le gain obtenu pour le joueur ou son adversaire. Les fonctions min et max retournent donc le gain (et non pas un coup à jouer comme max_min).
Il est important de noter que lorsque l'on gagne ou que l'on perd, il ne faut pas retourner le gain du joueur ou de son adversaire mais une valeur beaucoup plus forte, comme par exemple :
- +1000 si on gagne
- -1000 si on perd
Dans le cas de l'Awalé, le gain maximal étant de 48 (cas où on a ramassé toutes les billes) ou de -48 (l'adversaire a ramassé toutes les billes), il suffirait de prendre 49 pour indiquer une victoire et -49 pour une défaite.
// Algorithme min/max, pseudo code
// ------------------------------------------------------------------
//
// Fonction principale pour laquelle on tente de trouver quel
// meilleur coup jouer pour le joueur passé en paramètre du
// sous-programme
//
// jeu : situation de jeu
// joueur : joueur pour lequel on tente de trouver le meilleur coup
// jouable
//
// On retourne le meilleur coup jouable
//
// ------------------------------------------------------------------
fonction max_min( jeu, joueur ) : coup à jouer
meilleur_coup = ?
meilleur_score = -INFINI
pour tout coup jouable du joueur à partir de jeu faire
copie_jeu = réaliser une copie du jeu
joue coup pour copie_jeu
score = min( copie_jeu, joueur, adversaire(joueur), 1 )
// on cherche le gain maximum
si score > meilleur_score alors
meilleur_score = score
meilleur_coup = coup
fin si
fin pour
retourne meilleur_coup
fin fonction
// ------------------------------------------------------------------
// Fonction de minimisation lorsque l'adversaire joue
//
// jeu : situation de jeu
// joueur : joueur pour lequel on tente de trouver le meilleur coup
// jouable
// adversaire : adversaire du joueur
// profondeur : profondeur du coup joué
//
// ------------------------------------------------------------------
fonction min( jeu, joueur, adversaire, profondeur )
si profondeur = profondeur_max ou si on ne peut plus joueur alors
si on ne peut plus jouer alors
si gagnant == joueur alors
retourner +1000 // on gagne
sinon
retourner -1000 // on perd
sinon
// évaluation du gain
retourner f( jeu )
fin si
sinon
meilleur_score = +INFINI
pour tout coup jouable par l'adversaire à partir de jeu faire
copie_jeu = réaliser une copie du jeu
joue coup pour copie_jeu
score = max( copie_jeu, joueur, joueur, profondeur + 1 )
// on cherche le gain minimum pour l'adversaire
si score < meilleur_score alors
meilleur_score = score
fin si
fin pour
retourner meilleur_score
fin si
fin fonction
// ------------------------------------------------------------------
// Fonction de maximisation lorsque le joueur joue
// ------------------------------------------------------------------
fonction max( jeu, joueur, adversaire, profondeur )
si profondeur = profondeur_max ou si on ne peut plus joueur alors
si on ne peut plus jouer alors
si gagnant == joueur alors
retourner +1000 // on gagne
sinon
retourner -1000 // on perd
sinon
// évaluation du gain
retourner f( jeu )
fin si
sinon
meilleur_score = -INFINI
pour tout coup jouable par le joueur à partir de jeu faire
copie_jeu = réaliser une copie du jeu
joue coup pour copie_jeu
score = min( copie_jeu, joueur, adversaire(joueur), profondeur + 1 )
// on cherche le gain maximum
si score > meilleur_score alors
meilleur_score = score
fin si
fin pour
retourner meilleur_score
fin si
fin fonction
Comme on l'a déjà précisé, la fonction d'évaluation f consiste à retourner la différence entre le grenier du joueur qu'on désire faire gagner et le grenier de son adversaire.
L'analyse montre qu'il est intéressant de jouer sur plusieurs niveaux et avoir une profondeur assez grande afin de pouvoir trouver les coups les plus intéressants.
Cependant, il se peut que l'on perde quand même, si on a examiné les coups jusqu'à une profondeur $p$, mais qu'à la profondeur $p+1$, c'est l'adversaire qui peut jouer un coup qui lui permet de récolter un nombre important de billes ou de gagner.
Plus on augmente la profondeur de recherche plus on dépensera de temps à chercher une potentielle solution intéressante.
Pour un programme que j'ai écrit en C++ et exécuté sur un AMD Ryzen 5 5600G, on obtient les temps d'exécution suivants au début du jeu :
| profondeur | temps de calcul (s) |
| 12 | 2 à 3 |
| 13 | 11 à 14 |
| 14 | 37 à 62 |
| 15 | 170 à 300 |
1.3.2. alpha / beta
La technique ou l'heuristique de coupe alpha/beta permet d'éviter le développement de certaines branches de l'arbre de recherche qui seront de toute manière infructueuses. On diminue donc en conséquence le temps de calcul par rapport au min/max
- les coupes alpha se font au niveau MIN
- les coupes beta se font au niveau MAX
Si la valeur d'un noeud de niveau MIN est plus petite que la valeur de niveau MAX du noeud supérieur, qu'elles que soient les valeurs suivantes au niveau MIN, elles ne changeront pas la valeur MAX du noeud supérieur.
voir Enseignement LIG MIN/MAX Alpha/Beta.
1.3.3. Application morpion 3x3
Le système de valeurs pour l'évaluation (fonction $f$) est défini comme suit :
- 30 ou -30 si on a une 3 pions alignés
- -9 ou 9 si on en a 2 pions et ne position vie
- -6 ou 6 sin on a 1 pion et deux positions vides
- dans les autres cas on a 0
| Forme | Coût |
| |
0 |
| |
0 |
| |
-6 |
| |
-6 |
| |
-6 |
| |
-9 |
| |
-9 |
| |
-9 |
| |
-30 |
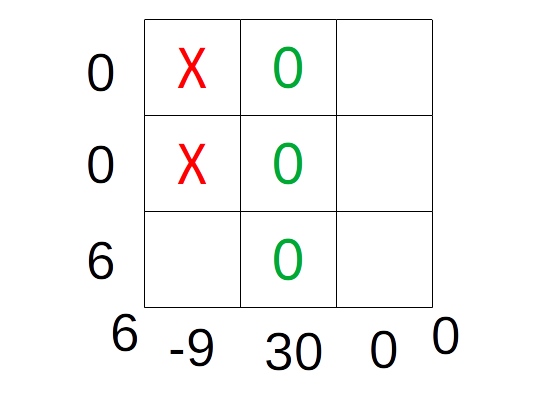
Figure : morpion, score d'un état du jeu
Examinons le comportement de l'algorithme MIN/MAX sur un état du jeu du morpion 3x3 :

Figure : morpion, min/max de profondeur 2
Exercice 1.2
Résoudre le problème du morpion (Tic Tac Toe) en utilisant une méthode de type min/max :
1.4. Jeu de type Cryptarithme
Un cryptarithme ou jeu cryptarithmétique est un casse-tête numérique et logique qui consiste en une équation mathématique où les lettres doivent être remplacées par des chiffres, deux lettres ne pouvant pas avoir la même valeur. L'un des plus connu car probablement le plus ancien est le problème $SEND + MORE = MONEY$

On trouvera de nombreux exemples de cryptarithmes sur cette page comme :
- $HUIT + HUIT = SEIZE$
- $UN + UN + NEUF = ONZE$
1.4.1. CSP
Pour résoudre ce genre de problème il est possible de le formuler comme une CSP (Constraint Satisfaction Problem) pour lequel on doit définir :
- des domaines de valeurs : $D = \{ d_1, ..., d_m \}$
- des variables : $V = \{ v_1, ..., v_n \}$
- des contraintes $C = \{ c_1, ..., c_k \}$ exprimées entre les variables
Pour $SEND + MORE = MONEY$, on a donc :
- $D = \{ d_1, d_2 \}$ avec $d_1 = \{ 0, 1 \}$ et $d_2 = \{ 0, ..., 9 \}$
- $V = \{ S, E, N, D, M, O, R, Y, R1, R2, R3, R4 \}$
- les variables $\{ S, E, N, D, M, O, R, Y \}$ prennent leurs valeurs dans $d_2$
- les retenues $\{ R1, R2, R3, R4 \}$ prennent leurs valeurs dans $d_1$
- des contraintes $C = \{ c_1, c_2, c_3, c_4 \}$ sont les suivantes :
- $c1$ (addition) : $D + E = Y + 10 × R1$
- $c2$ (addition) : $R1 + N + R = E + 10 × R2$
- $c3$ (addition) : $R2 + E + O = N + 10 × R3$
- $c4$ (addition) : $R3 + S + M = O + 10 × R4$
- $c5$ (égalité) : $R4 = M$
- $c6$ (alldiff) : $S, E, N, D, M, O, R, Y$
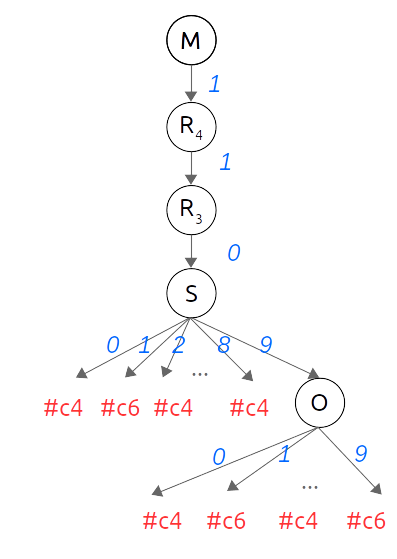
1.4.2. Stratégies
la résolution peut être plus ou moins longue en fonction de deux critères :
- l'ordre dans lequel on traite les variables
- l'ordre dans lequel on traite les valeurs à affecter aux variables
Par exemple dans le cas de $SEND + MORE = MONEY$, il est préférable de commencer par $M$ qui ne peut prendre que deux valeurs : 0 ou 1.
Exercice 1.3
Projet de programmation
Ecrire un programme qui permet de résoudre les problèmes cryptarithmétiques étant donné les paramètres en ligne de commande :
\$ ./cryptarithme.exe SEND MORE MONEY
S = ...
E = ...
\$ ./cryptarithme.exe UN UN NEUF ONZE
U = ...
On définira les classes Variable, Domain et Constraint et on utilisera ces classes pour modéliser et résoudre le problème.
Le projet est a réaliser seul ou en binôme et devra être rendu pour le 10 Janvier 2020 par email sous forme d'un fichier .tgz qui contiendra :
- les fichiers sources
- un makefile afin de compiler automatiquement votre code et générer un exécutable
- éventuellement un README qui donnera des indications sur les spécificités de votre implantation
le fichier .tgz devra être nommé suivant les noms des développeurs (par exemple dupond_durand.tgz) et devra lors du désarchivage créer un répertoire avec les noms des développeurs (dupond_durand/...).