Ce site est en cours de reconstruction certains liens peuvent ne pas fonctionner ou certaines images peuvent ne pas s'afficher.
7. TP 7
Produit Matrice / Vecteur
7.1. Contexte
On s'intéresse au produit d'une matrice $4 × 4$ de floats par un vecteur de 4 floats qui est une opération souvent utilisée en modélisation 3D. Une matrice $4 × 4$ sera modélisée sous forme d'un tableau à une dimension de 16 floats et un vecteur sous forme d'un tableau à une dimension de 4 floats.
$$(\table a , b ; c , d ; )$$
$$[\table m_{0,0},\; m_{0,1},\; m_{0,2},\; m_{0,3}; m_{1,0},\; m_{1,1},\; m_{1,2},\; m_{1,3}; m_{2,0},\; m_{2,1},\; m_{2,2},\; m_{2,3}; m_{3,0},\; m_{3,1},\; m_{3,2},\; m_{3,3}; ] × [\table v_0; v_1; v_2; v_3; ] $$
$$ = [ \table m_{0,0} × v_0 \;+\; m_{0,1} × v_1 \;+\; m_{0,2} × v_2 \;+\; m_{0,3} × v_3; m_{1,0} × v_0 \;+\; m_{1,1} × v_1 \;+\; m_{1,2} × v_2 \;+\; m_{1,3} × v_3; m_{2,0} × v_0 \;+\; m_{2,1} × v_1 \;+\; m_{2,2} × v_2 \;+\; m_{2,3} × v_3; m_{3,0} × v_0 \;+\; m_{3,1} × v_1 \;+\; m_{3,2} × v_2 \;+\; m_{3,3} × v_3; ] = [ \table a; b; c; d; ] $$
On vous demande de comparer une version traditionnelle (voir code ci-après) traduite par le compilateur C avec une version assembleur x86 32 bits utilisant la FPU et trois versions assembleur x86 32 bits utilisant les unités vectorielles SSE.
On effectuera le calcul 1_000_000_000 fois (1 milliard).
7.2. Version FPU
On utilisera les instructions classiques :
7.3. SSE version 1
On réalise le calcul classique en utilisant :
en suivant le schéma directeur :
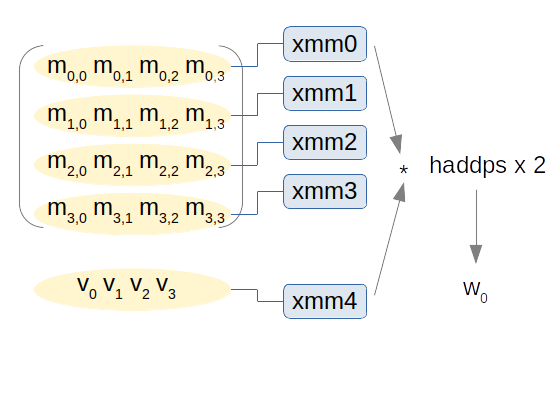
Par exemple pour obtenir $w_0$, on charge la première ligne de la matrice $m$ dans xmm0 et le vecteur $v$ dans xmm4. On multiplie xmm0 par xmm4, puis on réalise deux haddps sur xmm0.
7.4. SSE version 2
Dans la seconde version, on utilise l'instruction dpps (Dot Product of Packed Single Precision Floating-Point Values) au lieu de mulps et haddps.
On commence par charger :
- $v_0$ dans xmm0 en le recopiant 3 fois
- $v_1$ dans xmm1 en le recopiant 3 fois
- $v_2$ dans xmm2 en le recopiant 3 fois
- $v_3$ dans xmm3 en le recopiant 3 fois
On charge ensuite :
- la première ligne de la matrice transposée dans xmm4
- la deuxième ligne de la matrice transposée dans xmm5
- la troisième ligne de la matrice transposée dans xmm6
- la quatrième ligne de la matrice transposée dans xmm7
7.5. SSE version 3
Pour réaliser le calcul on transpose d'abord la matrice (le faire en C) et on effectue le calcul comme suit en utilisant MULPS, ADDPS, movss et shufps (Shuffle Packed Single-Precision Floating-Point Values)
$$[\table m_{0,0},\; m_{1,0},\; m_{2,0},\; m_{3,0}; m_{0,1},\; m_{1,1},\; m_{2,1},\; m_{3,1}; m_{0,2},\; m_{1,2},\; m_{2,2},\; m_{3,2}; m_{0,3},\; m_{1,3},\; m_{2,3},\; m_{3,3}; ] × { [\table v_0; v_0; v_0; v_0; ] , ··· , [\table v_3; v_3; v_3; v_3; ] } $$ $$ = [\table m_{0,0} × v_0, \;+\; m_{1,0} × v_0, \;+\; m_{2,0} × v_0, \;+\; m_{3,0} × v_0; m_{0,1} × v_1, \;+\; m_{1,1} × v_1, \;+\; m_{2,1} × v_1, \;+\; m_{3,1} × v_1; m_{0,2} × v_2, \;+\; m_{1,2} × v_2, \;+\; m_{2,2} × v_2, \;+\; m_{3,2} × v_2; m_{0,3} × v_3, \;+\; m_{1,3} × v_3, \;+\; m_{2,3} × v_3, \;+\; m_{3,3} × v_3; ∑=a, ∑=b, ∑=c, ∑=d; ] $$Pour les calculs on utilisera la matrice et le vecteur suivants :
float M[16] __attribute__((aligned(16))) = {
1, 2, 3, 4,
-1, -3, -6, -9,
4, 2, -5, 8,
-1, -2, -3, 7
};
float V[4] __attribute__((aligned(16))) = {1, 3, -2, 7 };
Le résultat doit être le vecteur W, dont les valeurs sont :
[29.0, -61.0, 76.0, 48.0]
Quelques résultats :
| méthode / CPU | Ryzen 5 3600 | Ryzen 7 1700X |
|---|---|---|
| 1 mvp_ref | 4.100 | 5.450 |
| 2 mvp_fpu | 7.620 | 11.250 |
| 3 mvp_sse_v1 | 5.010 | 5.550 |
| 4 mvp_sse_v2 | 5.760 | 4.500 |
| 5 mvp_sse_v3 | 3.140 | 3.600 |
| 6 mvp_sse_v4 | 3.060 | 3.610 |
Note : si on dispose du jeu d'instruction AVX/AVX2 on peut utiliser vbroadcastss au lieu de movss suivi de shufps.