9. TP - Méthodes de tri



9.1. Introduction

Dans ce TP, on s'intéresse à l'étude des méthodes de tri de tableaux d'entiers, notamment :

Les méthodes de tri à bulles et par insertion sont des méthodes de complexité en $O(n^2)$, plus précisément $(n^2)/2$ si $n$ est le nombre d'éléments à trier.

Par contre le tri rapide est une méthode de complexité en $O(n × log(n))$, ce qui la rend beaucoup plus rapide.

Complexité 10 100 1000 10000
$n² ÷ 2$ 50 5000 500000 50000000
$n × log(n)$ 23 461 6908 92103

Si on implante ces méthodes en C/C++ on s'aperçoit que la méthode de tri par insertion, bien que de complexité plus grande que celle du tri rapide, est plus efficace que le tri rapide pour des tailles de tableau $n ≤ 15$.

9.2. Implantation des méthodes de tri

Nous allons créer plusieurs fichiers :

9.2.1. Programme principal

Exercice 9.1

Créez le fichier tris.py, il comprendra une méthode main() ainsi qu'une fonction verifie_est_trie(t) qui vérifie si le tableau t passé en paramètre est bien trié en ordre croissant. Si ce n'est pas le cas, on lèvera une exception :

raise Exception("tableau non trié")

Une exception est une erreur qui peut être interceptée et traitée. Ici, comme l'exception ne sera pas traitée, elle termine le programme et le message d'erreur sera affiché.

9.2.2. Tri à bulles

Le tri à bulles est un tri assez simple : il consiste à faire remonter les éléments les plus grands vers les indices les plus hauts du tableau par échange de deux éléments consécutifs.

Procédure tri_à_bulles()
Entrée t tableau d'entiers
Sortie aucune, le tableau est trié en ordre croissant
Variables
globales		 aucune
Variables
locales		 i, j : variables de boucle
Description Etant donné un tableau de n éléments, faire remonter au fur et à mesure les éléments les plus grands vers les indices les plus hauts du tableau.
Le tableau possède $n$ éléments situés aux indices $0$ à $n-1$.
  1. n = taille(t)
  2.  
  3. pour i de 0 à n-2 faire
  4.     pour j = i+1 à n-1 faire
  5.         si t[i] > t[j] alors
  6.             échanger t[i], t[j]
  7.         fin si
  8.     fin pour
  9. fin pour
  10.  

Exercice 9.2

Créez un fichier tri_a_bulles.py et y définir une fonction tri(t) qui implante le tri à bulles. Attention, il faut bien appeler cette fonction tri et pas tri_a_bulles.

9.2.3. Tri par insertion

Le tri par insertion est un tri qui consiste à parcourir le tableau $t$ et à le trier au fur et à mesure pour que les éléments soient dans l'ordre croissant. Le tri par insertion se fait sur place. Ainsi, à l'étape $k$, les $k–1$ premiers éléments du tableau sont triés et on insère le $k$-ième élément à sa place parmi les $k$ premiers éléments.

Procédure tri_par_insertion()
Entrée t tableau d'entiers
Sortie aucune, le tableau est trié en ordre croissant
Variables
globales		 aucune
Variables
locales
  • i, j : variables de boucle
  • cle : valeur à replacer
Description cf. description ci-dessus.
  1. n = taille(t)
  2.  
  3. pour i de 1 à n-1 faire
  4.     # mémoriser t[i] dans cle
  5.     cle = t[i]
  6.  
  7.     # décaler les éléments t[0] à t[i-1] qui sont plus grands que cle,
  8.     # en partant de t[i-1]
  9.     j = i - 1
  10.     tant que j >= 0 et t[j] > cle faire
  11.         t[j+1] = t[j]
  12.         j = j - 1
  13.     fin tant que
  14.    
  15.     t[j+1] = cle
  16. fin pour

Exercice 9.3

Créez un fichier tri_par_insertion.py et y définir une fonction tri(t) qui implante le tri par insertion. Attention, il faut bien appeler cette fonction tri et pas tri_par_insertion.

9.2.4. Tri rapide (Quicksort)

Le tri rapide est un algorithme de tri inventé par C.A.R. Hoare en 1961 et fondé sur la méthode de conception diviser pour régner. La méthode consiste à placer un élément du tableau (appelé pivot) à sa place définitive, en permutant tous les éléments de telle sorte que tous ceux qui sont inférieurs au pivot soient à sa gauche et que tous ceux qui sont supérieurs au pivot soient à sa droite.

On va donner ici une méthode très simple basée sur ce principe mais qui n'est pas la plus optimale. Elle consiste à créer des sous-tableaux et à retourner le tableau réordonné.

fonction tri_rapide()
Entrée t tableau d'entiers
Sortie tableau d'entiers
Variables
globales		 aucune
Variables
locales
  • pivot : valeur pivot choisie au milieu du tableau
  • tinf : sous tableau des valeurs inférieures au pivot
  • tegal : sous tableau des valeurs égales au pivot
  • tsup : sous tableau des valeurs supérieures au pivot
Description cf. description ci-dessus.
  1. n = taille(t)
  2.  
  3. si n <= 1 alors
  4.     retourne t
  5. sinon
  6.     pivot = t[ taille(t) / 2]
  7.  
  8.     tinf, tegal, tsup : tableaux d'entiers
  9.  
  10.     pour i de 0 à n-1 faire
  11.         si t[i] < pivot alors
  12.             tinf.ajouter(t[i])
  13.         sinon si t[i] > pivot alors
  14.             tsup.ajouter(t[i])
  15.         sinon
  16.             tegal.ajouter(t[i])
  17.         fin si
  18.  
  19.     retourne tri(tinf) + tegal + tri(tsup)
  20. fin si

Exercice 9.4

Créez un fichier tri_rapide.py et y définir une fonction tri(t) qui implante le tri rapide. Attention, il faut bien appeler cette fonction tri et pas tri_rapide.

9.2.5. Test des fonctions de tri

Exercice 9.5

Dans le programme principal tris.py testez les 3 méthodes de tri et vérifier que les tableaux obtenus après appel de la fonction de tri sont bien triès par ordre croissant grâce à la fonction verifie_est_trie(t) .

9.3. Comparaison des méthodes de tri

On va maintenant tester le temps d'exécution de chacune des méthodes de tri pour des tableaux de tailles différentes.

On prendra les tailles suivantes $[100, 1000, 10000, 20000]$ et on générera des tableaux avec des valeurs aléatoires.

Exercice 9.6

Dans le programme principal tris.py, créez une méthode evaluation_tri_a_bulles() qui pour chaque taille à tester, évalue le temps d'exécution du tri. Pour cela utiliser le package time et la méthode time comme suit :

import time
# ...    
debut = time.time()
# ... code à chronométrer
fin = time.time()
temps_d_execution = fin - debut

Les temps obtenus sont en secondes.

Le sous-programme evaluation_tri_a_bulles() retournera un tableau/liste des temps d'exécution que l'on stockera dans une variable t1.

Exercice 9.7

Dans le programme principal tris.py, créez une méthode evaluation_tri_par_insertion() qui pour chaque taille à tester, évalue le temps d'exécution du tri.

Le sous-programme evaluation_tri_par_insertion() retournera un tableau/liste des temps d'exécution que l'on stockera dans une variable t2.

Exercice 9.8

Dans le programme principal tris.py, créez une méthode evaluation_tri_rapide() qui pour chaque taille à tester, évalue le temps d'exécution du tri.

Le sous-programme evaluation_tri_rapide() retournera un tableau/liste des temps d'exécution que l'on stockera dans une variable t3.

9.3.1. Comparaison visuelle

Utilisez matplotlib afin de générer un graphique des 3 séries de données.

  1. import matplotlib.pyplot as plt
  2.  
  3. tailles = [100, 1000, 10000, 20000]
  4.  
  5. # taille de la figure
  6. plt.figure(figsize=(8, 5))  
  7.  
  8. plt.plot(tailles, t1, label='à bulles', marker='o')  
  9. plt.plot(tailles, t2, label='insertion', marker='s')  
  10. plt.plot(tailles, t3, label='rapide', marker='x')  
  11.  
  12. # Label the axes
  13. plt.xlabel('Tailles')
  14. plt.ylabel('Temps d\'exécution (s)')
  15.  
  16.  
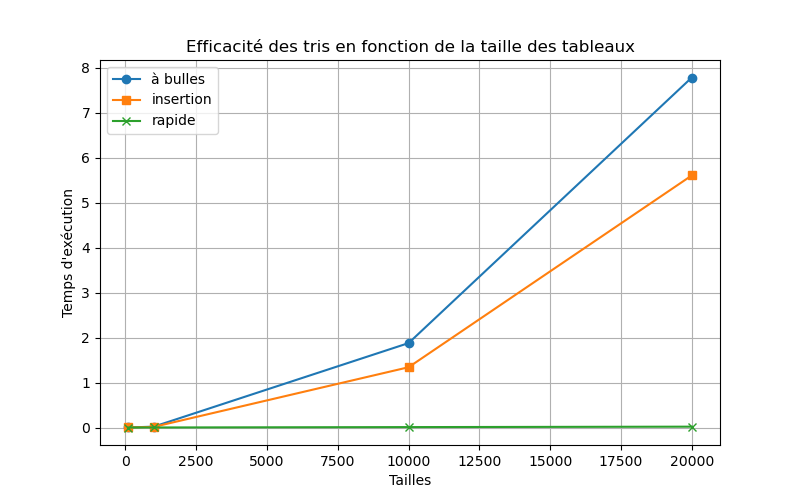
  17. plt.title('Efficacité des tris en fonction de la taille des tableaux')
  18. plt.legend()
  19.  
  20.  
  21. plt.grid(True)
  22. plt.show()

Vous devriez obtenir un graphique similaire à celui-ci :

graphique