8. TP - Matplotlib
8.1. Introduction
Dans ce TP, on s'intéresse à la librairie matplotlib qui permet de réaliser des graphiques et dont la documentation peut être trouvée à cette adresse matplotlib.org.
8.2. Tracé d'une fonction (plot)
On désire tracer une fonction réelle. On utilise pour cela la fonction plot.
On peut également utiliser la fonction savefig afin de sauvegarder un graphique.
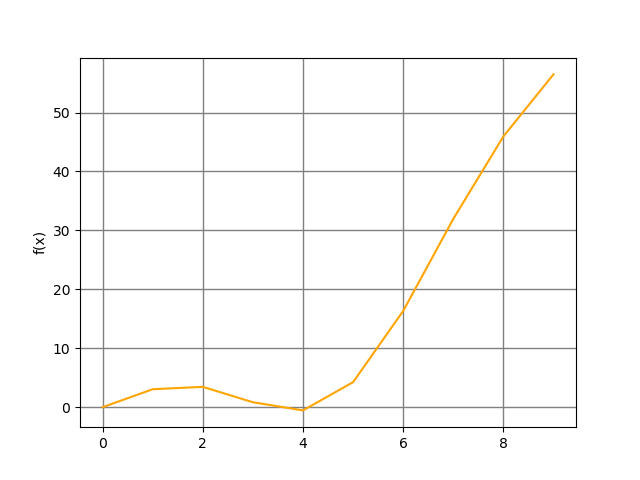
8.2.1. Sans numpy
Voici une première version sans numpy pour l'évaluation de la fonction. On utilise la fonction sinus et il est donc nécessaire de faire appel au module math :
- # import des libraries / packages
- import matplotlib.pyplot as plt
- import math
- # fonction à dessiner
- def f(x):
- return x*x-3*x+6*math.sin(x)
- # valeurs pour x, on utilise pas numpy
- # On génère 10 valeurs entières de 0 à 9
- x_values = range(0, 10)
- print(x_values)
- # on calcule les valeurs de y pour chaque x
- y_values = [f(x) for x in x_values]
- print(y_values)
- # on dessine la fonction
- plt.plot(x_values, y_values, color='orange')
- plt.grid(color='grey', linestyle='-', linewidth=1)
- plt.ylabel('f(x)')
- plt.savefig('img/plot_function_without_numpy.png')
- plt.show()
On calcule les valeurs pour x (x_values) puis celles de y(y_values) et enfin on dessine la courbe en utilisant ces valeurs.
8.2.2. Avec numpy
Voici une seconde version avec numpy pour l'évaluation de la fonction ce qui permet de simplifier la génération des valeurs à la fois pour x et pour y. On notera l'utilisation de np.sin(x) au lieu de math.sin(x) dans le calcul de la fonction $f$ :
- # import des libraries / packages
- import matplotlib.pyplot as plt
- import math
- import numpy as np
- # fonction à dessiner
- def f(x):
- return x * x - 3 * x + 6 * np.sin(x)
- # valeurs pour x, on utilise numpy
- # On génére 100 valeurs etre 0 à 100 (compris)
- x_values = np.linspace(0, 10, 100)
- print(x_values)
- # on génère y_values avec la fonction f
- y_values = f(x_values)
- print(y_values)
- # on dessine la fonction
- plt.plot(x_values, y_values, color='green')
- plt.grid()
- plt.ylabel('f(x)')
- plt.show()
On remarquera que l'on utilise la fonction linspace de numpy afin de générer des valeurs dans l'intervalle [0,10].
Exercice 8.1
Afficher le graphique de la fonction :
$$ f1(x) = (√|x -3|) × x $$dans l'intervalle $[-10,10]$ en générant une centaine de valeurs (utiliser numpy).
Exercice 8.2
Afficher sur le même graphique les fonctions :
$$\{\table f1(x) = x; f2(x) = x × \log(x); f3(x) = x × x; $$dans l'intervalle $[1,10]$ en générant une centaine de valeurs (utiliser numpy)
Afficher chacune des fonctions avec une couleur différence (red, green, blue) et une légende (
Exercice 8.3
Créez dans le fichier
Vous devriez obtenir l'image suivante :
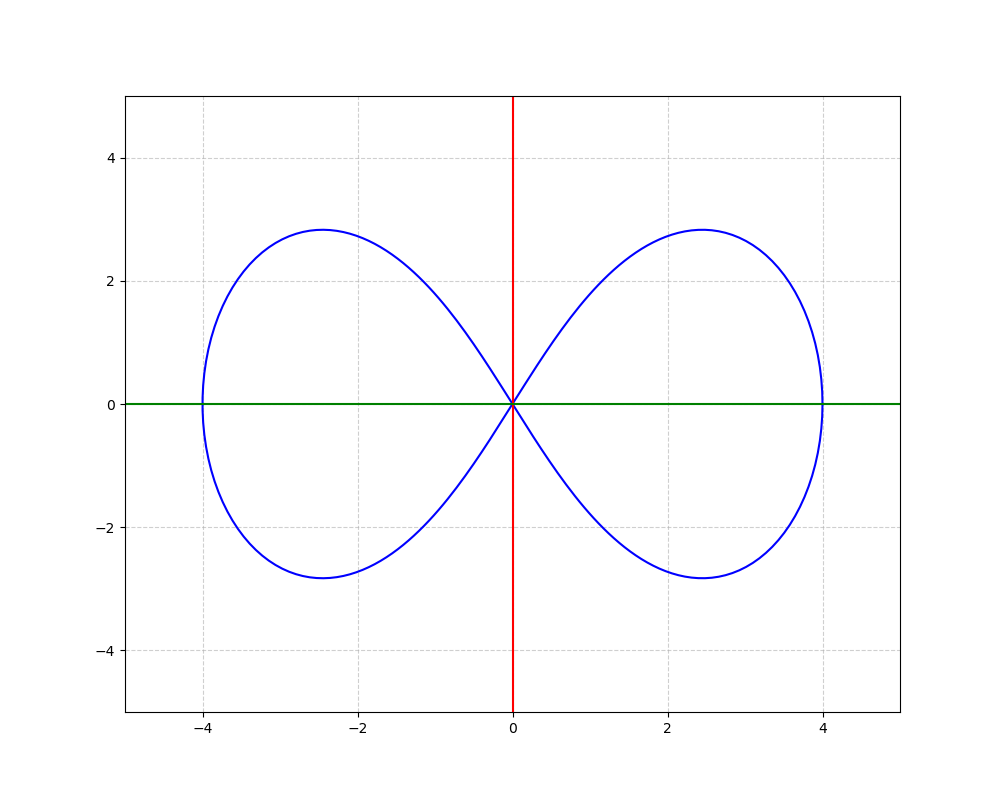
- CODE
- lemniscate.py
- import numpy as np
- import matplotlib.pyplot as plt
- t = np.linspace(0, 2 * np.pi, 250)
- # x =
- # y =
- # Tracer le graphique
- plt.figure(figsize=(10, 8))
- plt.plot(x, y, label='x(t),y(t)', color='blue')
- plt.ylim(-10, 10)
- #....
- # Afficher le graphique
- plt.grid(True, linestyle='--', alpha=0.6)
- plt.show()
8.3. Données en barres (bar, barh)
Il est parfois nécessaire de modéliser les données sous forme graphique et les graphes qui utilisent des barres permettent de rendre compte d'une donnée numérique associée à une catégorie.
A titre d'exemple, considérons que nous avons interrogé 75 personnes et que nous leur avons demandé quel langage de programmation elles utilisent le plus souvent. Voici les résultats de ce sondage :
- C++ : 20 personnes
- Ruby : 10 personnes
- Python : 30 personnes
- Php : 15 personnes
8.3.1. Barres verticales (bar)
On peut représenter ces données sous forme de barres verticales ce qui permet tout de suite de voir quel langage est le plus utilisé et quel langage est le moins utilisé, est-ce qu'un langage se démarque des autres, etc. Sur quatre données cela est inutile mais sur des dizaines de données cela est beaucoup plus pratique.
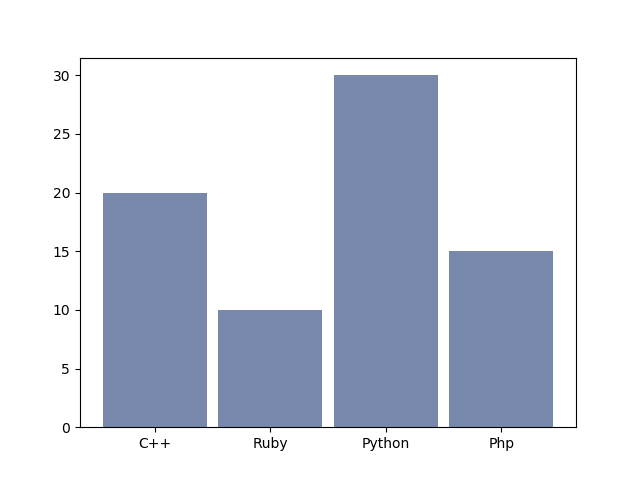
Voici le code correspondant à ce graphique :
- CODE
- plot_bar_chart.py
- import matplotlib.pyplot as plt
- from matplotlib import cm
- import math
- import numpy as np
- # langages de programmation
- y_labels = [ 'C++', 'Ruby', 'Python', 'Php' ]
- # x_values indique sur l'axe des x où on doit situer
- # la barre verticale
- x_values = [ 1, 2, 3, 4 ]
- # y_values représentent les données associées à chaque langage
- y_values = [ 20, 10, 30, 15 ]
- plt.bar(x=x_values, height=y_values, width=0.9,
- color='#7788aa', tick_label = y_labels)
- plt.savefig('img/plot_bar_chart.png')
- plt.show()
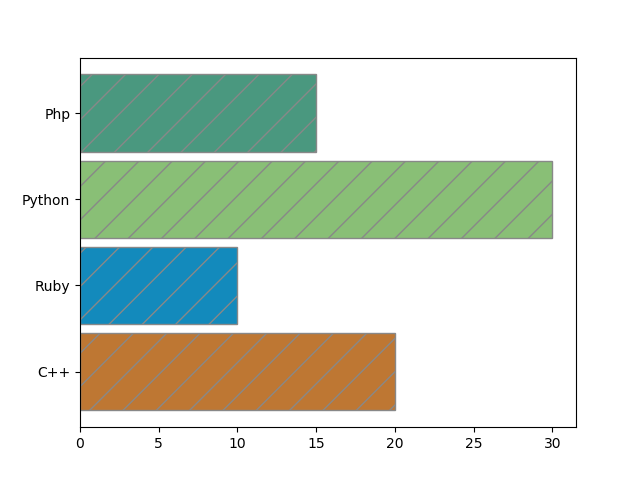
8.3.2. Barres horizontales (barh)
On peut procéder de la même manière mais avec des barres horizontales.
- CODE
- plot_barh_chart.py
- import matplotlib.pyplot as plt
- from matplotlib import cm
- import math
- import numpy as np
- # langages de programmation
- x_labels = [ 'C++', 'Ruby', 'Python', 'Php' ]
- x_values = [ 1, 2, 3, 4 ]
- y_values = [ 20, 10, 30, 15 ]
- plt.barh(y=x_values, width=y_values, height=0.9,
- color=['#be7733', '#138ABc', '#89bf76', '#4A987f'],
- tick_label = x_labels, hatch="/",
- edgecolor='#888888')
- plt.savefig('img/plot_barh_chart.png')
- plt.show()
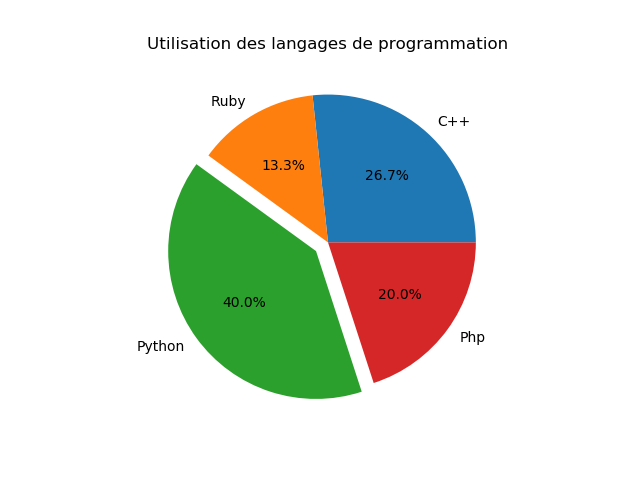
8.4. Camembert (pie)
Le camembert ou (pie chart en anglais) permet également, tout comme les graphes de barres, de donner une idée de la répartition des données mais sous forme de pourcentage.
- CODE
- plot_pie_chart.py
- import matplotlib.pyplot as plt
- from matplotlib import cm
- import math
- import numpy as np
- x_labels = [ 'C++', 'Ruby', 'Python', 'Php' ]
- x_values = [ 20, 10, 30, 15 ]
- x_explode = (0, 0, 0.1, 0)
- plt.pie(x_values, labels=x_labels, autopct='%1.1f%%', explode=x_explode)
- plt.title("Utilisation des langages de programmation")
- plt.savefig('img/plot_pie_chart.png')
- plt.show()
Exercice 8.4
Afficher un graphique sous forme de camembert pour un ensemble de valeurs générées
aléatoirement avec une dizaine de valeurs. Faire en sorte que la valeur la plus
grande soit détachée du graphique.
8.5. Graphe de points (scatter)
8.5.1. Exemple classique
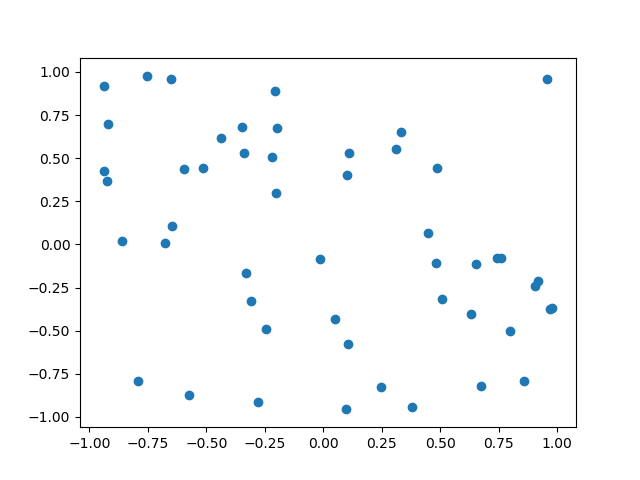
Dans certains cas, on dispose de données éparses et on désire les afficher afin de savoir si elle sont corrélées.
Voici un premier exemple généré de manière aléatoire en utilisant numpy :
- import matplotlib.pyplot as plt
- import math
- import numpy as np
- x_values = np.random.uniform(-1.0, 1.0, 50)
- y_values = np.random.uniform(-1.0, 1.0, 50)
- plt.scatter(x_values, y_values)
- plt.savefig('img/plot_scatter_random.png')
- plt.show()
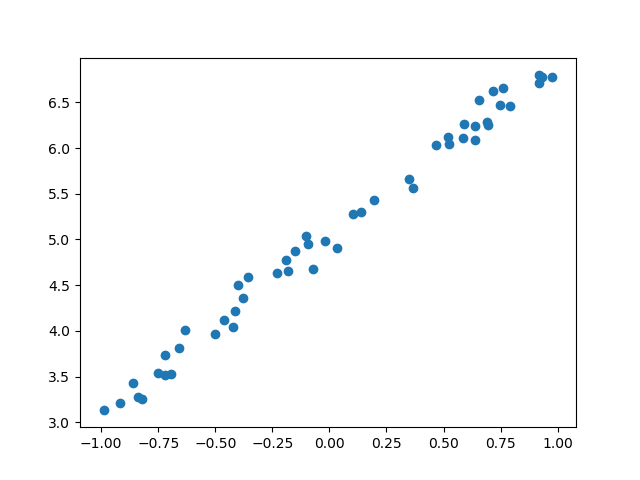
Le deuxième exemple utilise une fonction linéaire pour associer les données :
Exercice 8.5
Afficher un graphique sous forme "scatter plot" pour des valeurs de $x$ dans l'intervalle
$[0,10]$ et qui correspondent à une fonction $f(x) = x*x$ pour laquelle on aura introduit
de petites variations par rapport à la fonction entre -2 et +2.
Faire en sorte d'afficher la courbe en vert et de modifier le marker en '+'.
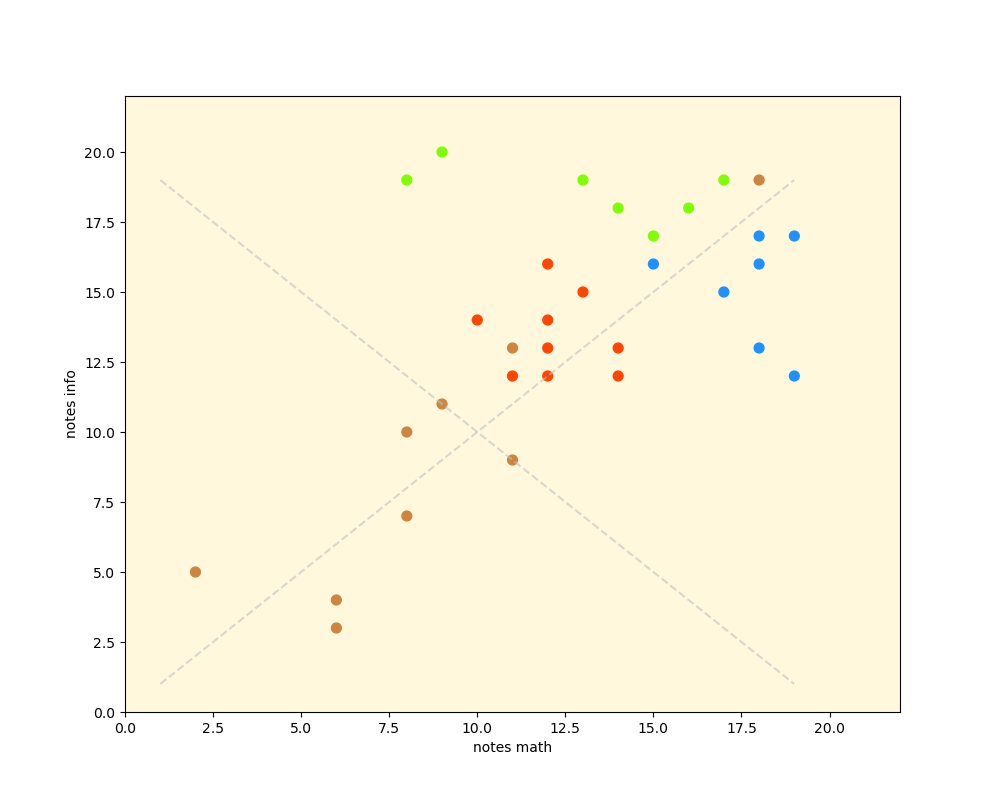
8.5.2. Exemple des étudiants de l'université de Malibu
On dispose d'un fichier mu.csv qui contient pour différents étudiants qui sont inscrits en première année à l'université de Malibu en Californie, trois champs : provenance (état), moyenne en mathématiques, moyenne en informatique
arizona,14,13
california,18,17
nevada,8,19
other,6,3
arizona,14,12
arizona,12,13
...
Quatre états sont représentés : Californie, Arizona, Nevada et Other pour les étudiants en provenances d'autres états.
On désire réaliser un graphique représentatif comme celui-ci:
- identifiez de quel état proviennent les étudiants qui sont les meilleurs en mathématiques ou en informatique
- de quel état proviennent les étudiants qui sont les moins bons
Exercice 8.6
Etudiez le contenu du fichier
- on récupère le fichier et on extrait les données suivants trois colonnes :
etats ,notes_math ,notes_info - on affiche la moyenne de
notes_math etnotes_info - on remplace les noms des états par des chiffres, par exemple si on prend
l'ordre alphabétique :
- arizona : 0
- california : 1
- nevada : 2
- other : 3
Voici le code du fichier :
- CODE
- malibu.py
- import numpy as np
- import matplotlib.pyplot as plt
- import matplotlib.colors as col
- from matplotlib.colors import ListedColormap
- import matplotlib.patches as mpatches
- # définition de couleurs
- colors = ['orangered', 'dodgerblue', 'chartreuse', 'peru' ]
- # création d'une colormap : 0 correspond à 'orangered', 1 à 'dodgerblue', etc.
- jmr_cmap = ListedColormap(colors)
- def lire_fichier(nom_fichier):
- """
- Lit un fichier et retourne ses lignes sous forme de liste.
- Args:
- chemin_fichier (str): Le chemin du fichier à lire.
- Returns:
- list: Liste contenant les lignes du fichier.
- """
- try:
- with open(nom_fichier, 'r', encoding='utf-8') as fichier:
- lignes = fichier.read()
- return lignes
- except FileNotFoundError:
- print(f"Erreur : Le fichier '{nom_fichier}' n'existe pas.")
- return []
- except Exception as e:
- print(f"Erreur inattendue : {e}")
- return []
- def main():
- # Lecture du fichier
- nom_fichier = "mu.csv"
- texte = lire_fichier(nom_fichier)
- lignes = texte.split('\n')
- print(lignes)
- # Créer les vecteurs de données
- notes_math = []
- notes_info = []
- etats = []
- for ligne in lignes:
- if len(ligne) != 0:
- colonnes = ligne.split(',')
- notes_math.append(float(colonnes[1]))
- notes_info.append(float(colonnes[2]))
- etats.append(colonnes[0])
- etats = np.array(etats, dtype=str)
- etats, indices_etats = np.unique(etats, return_inverse=True)
- # ['arizona' 'california' 'nevada' 'other']
- print(f"etats={etats}")
- # [0 1 2 3 1 0 ... 3 3 3 3]
- print(f"indices etats={indices_etats}")
- # [13.0, 17.0, 19, ... 5.0, 4.0, 7.0]
- print(f"notes en informatique={notes_info}")
- # [14.0, 18.0, ... 2.0, 6.0, 8.0]
- print(f"notes en mathématiques={notes_math}")
- moyenne_info = np.average(notes_info)
- moyenne_math = np.average(notes_math)
- # 13.53
- print(f"moyenne info={moyenne_info:5.2f}")
- # 12.56
- print(f"moyenne math={moyenne_math:5.2f}")
- plt.figure(figsize=(10, 8))
- # Graphique pour la répartition des notes en informatique
- plt.xlabel(f"notes informatiques, moyenne={moyenne_info:5.2f}")
- plt.ylabel("notes")
- plt.xlim(0,21)
- # retourne les valeurs uniques et leur nombre d'occurrences
- notes_info_echantillon, notes_info_occurrences = np.unique(notes_info, return_counts=True)
- plt.ylim(0,np.max(notes_info_occurrences)+1)
- plt.bar(notes_info_echantillon, notes_info_occurrences, color='skyblue', edgecolor='black')
- plt.show()
- # Graphique pour la répartition des notes en mathématiques
- plt.figure(figsize=(10, 8))
- plt.xlabel(f"notes mathématiques, moyenne={moyenne_math:5.2f}")
- plt.ylabel("notes")
- plt.xlim(0,21)
- # retourne les valeurs uniques et leur nombre d'occurrences
- notes_math_echantillon, notes_math_occurrences = np.unique(notes_math, return_counts=True)
- plt.ylim(0,np.max(notes_math_occurrences)+1)
- plt.bar(notes_math_echantillon, notes_math_occurrences, color='lightgreen', edgecolor='black')
- plt.show()
- # Graphique avec notes en informatique et notes en mathématiques
- plt.figure(figsize=(10, 8))
- ax = plt.axes()
- ax.set_facecolor("cornsilk")
- plt.xlabel("notes math")
- plt.ylabel("notes info")
- plt.xlim(0,22)
- plt.ylim(0,22)
- x=np.arange(1,20)
- y1=x
- y2=20-x
- plt.plot(x, y1, "silver", linestyle='--', alpha=0.6)
- plt.plot(x, y2, "silver", linestyle='--', alpha=0.6)
- # Création de la légende
- plt.scatter(notes_math, notes_info, c=indices_etats, cmap=jmr_cmap, s=50)
- patches = [mpatches.Patch(color=jmr_cmap(i), label=etats[i]) for i in range(len(etats))]
- plt.legend(handles=patches, title="État d'origine")
- plt.show()
- if __name__ == "__main__":
- main()