7. TP - NReines

7.1. Introduction

Le problème des N-reines consiste à placer sur un échiquier de $N × N$ cases, $N$ reines, une reine par colonne (ou par rangée) de manière à ce qu'aucune reine ne soit en prise avec une autre.

Ce problème a été posé en 1848 par un joueur d'échecs allemand, Max Bezzel, pour $N = 8$.

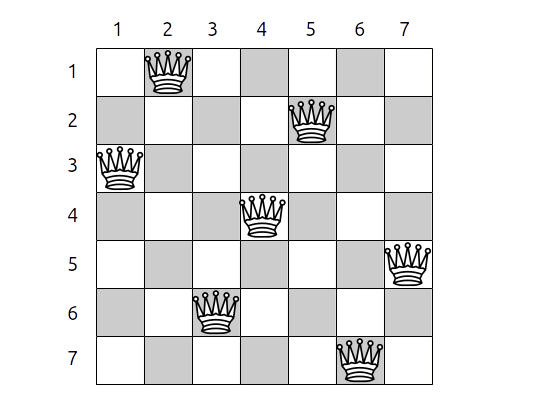
n-reines, n-queens
Solution pour N=7

Voici le nombre solutions en fonction de $N$ :

Problème des N_reines, nombre de solutions
N	Solutions
2	0
3	0
4	2
5	10
6	4
7	40
8	92
9	352
10	724
11	2680
12	14200

Exercice 7.1

La complexité de ce problème est de l'ordre de $O(N!)$. Si on raisonne simplement, on a $N$ possibilités de choix pour la première reine, puis $N-1$ (en fait $N-2$) pour la seconde, etc.

7.2. Résolution

Nous allons étudier plusieurs algorithmes de résolution du problème, à savoir :

méthode 1 : utilisation des permutations
méthode 2 :utilisation d'un échiquier et vérification des prises (récursif avec retour arrière)
méthode 3 :utilisation remplissage des cases en prises de l'échiquier (récursif avec retour arrière)
méthode 4 :utilisation de tableaux qui modélise les colonnes et diagonales (récursif avec retour arrière)

7.2.1. Méthode des permutations

Une première méthode issue du livre Python 3, les Fondamentaux du langage, Sébastien Chazallet, Editions ENI (page 428), utilise les permutations et vérifie que deux reines ne sont pas en prise en comparant le nombre d'éléments dans chaque ensemble de diagonales.

La méthode est concise et intéressante d'un point de vue intellectuel mais totalement inefficace car il faut tester chaque permutation, soit $N!$. Pour s'en convaincre, on consultera la section Résultats

n_reines_v1.py

"""
    Résolution du problème des N-Reines en passant
    en revue toutes les permutations possibles
 
    Pour chaque permutation (appelée xs) on
    évalue les diagonales occupées :
    - diagonales droites ou positives : y+x
    - diagonales gauches ou negatives : y-x
"""
 
from itertools import permutations
import time
import sys
 
 
# nombre de reines initial peut être modifié en appelant
# le programme avec un argument entier
N = 6
 
# nombre de permutations calculées : doit être égal à N!
nbr_permutations = 0
 
def resoudre(n):
    """
        Résolution du problème des N-Reines
        en passant en revue toutes les permutations possibles
    """
    global nbr_permutations
 
    # lignes : ys = [0,1,...,N-1]
    ys = range(n)
 
    # pour chaque permutation
    for xs in permutations(ys):
        nbr_permutations = nbr_permutations + 1
        # on compte les diagonales occupées
        diag_pos = set(y + xs[y] for y in ys)
        diag_neg = set(y - xs[y] for y in ys)
    
        if n == len(diag_pos) == len(diag_neg):
            yield xs
 
 
 
def main():
    """
        Fonction principale
    """
    global N
 
    if len(sys.argv) > 1:
        N = int(sys.argv[1])
 
 
    # chronométrage du temps de calcul
    t1 = time.time()
    liste_solutions = list(resoudre(N))
    ns = len(liste_solutions)
    t2 = time.time()
 
    print(f"nombre de reines={N}")
    print(f"permutations={nbr_permutations}")
    print(f"solutions={ns}")
    print(f"temps de calcul={t2-t1}s")
 
if __name__ == "__main__":
    main() 

On génère toutes les permutations possibles et on compte le nombre de diagonales positives et négatives :

les diagonales positives correspondent à : $y + x$
les diagonales négatives correspondent à : $y - x$

Par exemple, pour $N=4$, on trouvera une solution si $\text"diag_pos"$ et $\text"diag_neg"$ sont de taille $4$, cela signifie qu'il n'y a aucune reine en prise sur les diagonales :

ys=(0, 1, 2, 3)
xs=(1, 3, 0, 2)
diag_pos = {1, 2, 4, 5}
diag_neg = {1, 2, -2, -1}

Ici les reines sont placées en $(y=0,x=1)$, $(y=1,x=3)$, $(y=2,x=0)$ et $(y=3,x=2)$.

7.2.2. Méthode des prises sur l'échiquier

Le principe est simple : on modélise l'échiquier sous forme d'une matrice de $N$ par $N$ entiers.

initialiement la matrice est composée de 0
placer une reine sur l'échiquier consiste à assigner à la case correspondante la valeur de la reine (variant entre 1 et $N$)
on commence par la reine en ordonnée 1 (en fait 0), puis 2 (en fait 1), etc
à chaque étape on vérifie qu'il n'y a pas de prise :
- avec une reine située sur une ordonnée inférieure
- avec une diagonale positive supérieure
- avec une diagonale négative supérieure

Attention, en Python, le premier indice d'une liste sera 0 et non pas 1.

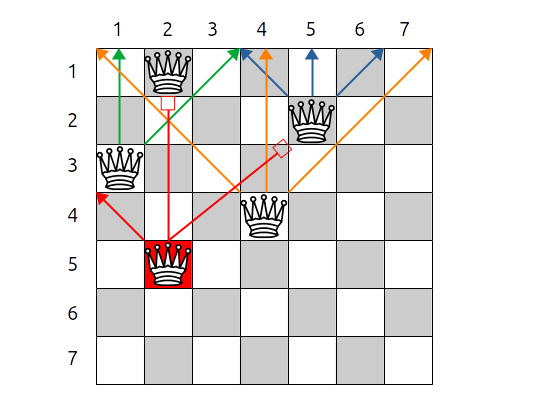
Sur la figure précédente, la reine en ligne 5, colonne 2 est en prise avec deux autres reines.

Exercice 7.2

Implantez la résolution en utilisant la méthode par vérification des prises. Créez un fichier appelé nreines_v2.py doté d'une méthode main qui vérifiera si un paramètre donnant la taille de l'échiquier est présent.

On utilisera une matrice échiquier de dimension $N× N$ cases intialisées à 0 ainsi que les méthodes suivantes :

trouve_les_solutions(echiquier, y:int) -> None qui recherche toutes les solutions au problème, on passe en paramètre l'échiquier et le numéro de la ligne ou placer la reine
existe_conflit(echiquier, y, x) -> bool qui vérifie que la reine en position $(y,x)$ sur l'échiquier n'est pas en prise avec une reine située sur un $y' < y$

Concernant trouve_les_solutions(echiquier, y:int), il s'agit d'un sous-programme récursif pour lequel si $y >= N$ on a trouvé une solution. Si $y < N$, il faut tester toutes les possibilités de placement pour $x$ variant de 1 à $N$ (où plutôt variane de 0 à $N-1$).

Pour la fonction existe_conflit(echiquier, y, x) il faut vérifier qu'il n'y a pas de reine sur la colonne où on place la reine (c'est à dire $x$), sur la diagonale gauche ($y' = y -1$ et $x'= x-1$) et sur la diagonale droite ($y' = y -1$ et $x'= x+1$).

7.2.3. Méthode de remplissage des prises de l'échiquier

Dans cette variante, dès qu'on place une reine, on affecte les cases de l'échiquier concernées par une prise de manière à indiquer quelles cases sont inutilisables par la suite pour le positionnement des reines suivantes.

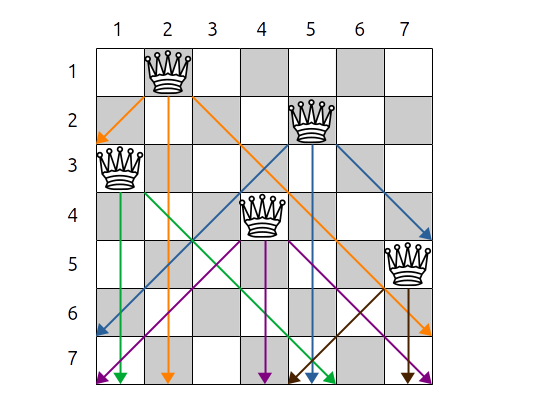
Exercice 7.3

Créez un fichier nreines_v3.py et implantez la résolution en utilisant la méthode par remplissage des prises. Il faudra créer deux méthodes place_reine(echiquier,y,x) et supprime_reine(echiquier,y,x).

7.2.4. Méthode des tableaux colonnes et diagonales

Au lieu d'utiliser un échiquier de $N$ par $N$ cases, on utilise trois tableaux d'entiers :

un tableau de $N+1$ cases qui représente les rangées
un tableau de $2N+1$ cases qui représentent les diagonales droites (positives) occupées
un tableau de $2N+1$ cases qui représentent les diagonales gauches (négatives) occupées

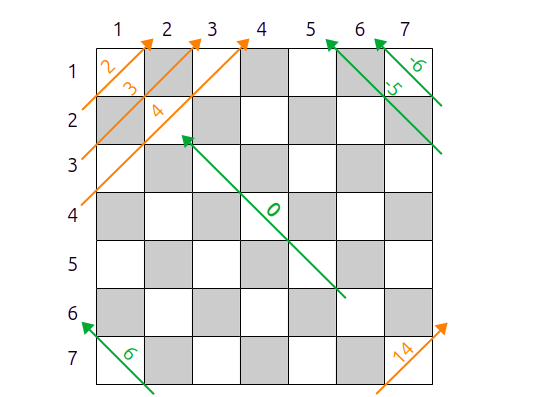
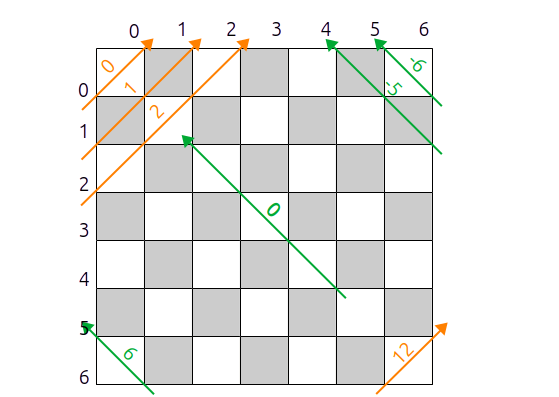
Diagonales positives (orange) et négatives (vert) en fonction des indices qui commencent à 1 ou à 0 pour $x$ et $y$.

Ces tableaux sont initialisés à True . Dés qu'on place une reine $y$ dans la colonne $x$, on positionne à $y$ la rangee et la diagonale correspondante :

rangees$[x]$ à False
droite$[y+x]$ à False
gauche$[N+y-x]$ à False
on peut placer une reine en $(y,x)$ si (range$[x]$ and droite$[y+x]$ and gauche$[N+y-x]$ == True)

Exercice 7.4

Implantez la résolution en utilisant la méthode par tableaux rangées et diagonales (droite et gauche) dans le fichier fichier nreines_v4.py .

7.3. Résultats

Voici quelques résultats sur AMD Ryzen 5 5600G. Vous pouvez comparez ces temps à ceux que vous obtenez sur les machines des salles de TP.

On a donc 5 implantations :

méthode 1 : utilisation des permutations
méthode 2 : utilisation d'un échiquier et vérification des prises (récursif avec retour arrière)
méthode 3 : remplissage des cases en prises de l'échiquier (récursif avec retour arrière)
méthode 4 : utilisation de tableaux qui modélisent les colonnes et diagonales (récursif avec retour arrière)
méthode 5 : implantation en C++ de la méthode 4

Problème des N_reines (de N=4 à 12), temps d'exécution en secondes pour chaque méthode sur AMD Ryzen 5 5600G.
N	Méthode 1	Méthode 2	Méthode 3	Méthode 4	Méthode 5
4	0.000	0.000	0.000	0.000	0.000
5	0.000	0.000	0.000	0.000	0.000
6	0.001	0.000	0.000	0.000	0.000
7	0.005	0.001	0.001	0.000	0.000
8	0.042	0.004	0.002	0.001	0.000
9	0.393	0.017	0.009	0.004	0.000
10	4.040	0.087	0.042	0.018	0.001
11	46.410	0.479	0.204	0.089	0.006
12	584.544	2.911	1.086	0.460	0.032
13	?	17.310	6.246	2.644	0.181

Problème des N_reines (de N=4 à 12), temps d'exécution en secondes pour chaque méthode sur Intel i5 12400F.
N	Méthode 1	Méthode 2	Méthode 3	Méthode 4	Méthode 5
4	0.000	0.000	0.000	0.000	0.000
5	0.000	0.000	0.000	0.000	0.000
6	0.001	0.000	0.000	0.000	0.000
7	0.007	0.001	0.001	0.000	0.000
8	0.048	0.005	0.003	0.001	0.000
9	0.444	0.025	0.014	0.005	0.001
10	4.335	0.121	0.061	0.020	0.003
11	49.813	0.733	0.304	0.102	0.011
12	629.373	23.926	8.898	3.003	0.233

On constate que concernant l'implantation en Python, la méthode 4 est la plus rapide. Cependant, cette même méthode, implantée en C++ (méthode 5) est encore bien plus rapide.

Page de Jean-Michel Richer