5. TP - Récursivité et problème du cavalier



5.1. Introduction

Certains traitements peuvent être définis sous forme de relation de récurrence. Par exemple les suites sont un exemple idiomatique de la récurrence.

La résolution de problèmes complexes nécessite souvent des sous-programmes récursifs afin de rechercher une solutions dans un espace donné.

C'est ce que nous allons voir avec la résolution du problème du cavalier.

5.2. Récursion et condition d'arrêt

On peut calculer une relation de récurrence mais si elle ne termine jamais on est confronté à un problème. C'est le cas par exemple en logique avec un problème comme :

$$\{\table f(a) ; ¬f(X) ∨ f(X) ; ¬f(b) $$

à partir de $f(a)$, on va générer $f(f(a))$, puis $f(f(f(a)))$, ... , $f^n(a))$ sans jamais s'arrêter.

En informatique une relation de récurrence est mise en oeuvre au travers de la récursivité. On parle de récursivité lorsqu'une fonction s'appelle ou lorsqu'une structure de données s'auto-référence.

Un sous-programme récursif doit comporter deux propriétés :

  • une relation de récurrence
  • une condition d'arrêt de la récurrence

Prenons l'exemple de la fonction factorielle : $n! = n × n-1 × … × 2 × 1$.

Ici la relation de récurrence est simple. Si on appelle $f(n) = n!$ alors :

L'implantation en Python est triviale :

  1. # factorielle.py
  2.  
  3. def factorielle(n : int) -> int:
  4. if n == 1:
  5.     return 1
  6. else:
  7.     return n * factorielle(n-1)
  8.  
  9.  
  10. for i in range(1, 11):
  11.     print(f"{i:2}! = {factorielle(i):>{10},}")

Exercice 5.1

A titre d'exercice écrire un programme Python nommé fibonacci.py qui affiche les 20 premiers termes de la suite de fibonacci implantée sous forme d'une fonction récursive :

  • $fibonacci(0) = 0$
  • $fibonacci(1) = 1$
  • $fibonacci(n) = fibonacci(n-1) + fibonacci(n-2)$

Vous devriez obtenir le résultat suivant :

fib( 1) =          1
fib( 2) =          1
fib( 3) =          2
fib( 4) =          3
fib( 5) =          5
fib( 6) =          8
fib( 7) =         13
fib( 8) =         21
fib( 9) =         34
fib(10) =         55
fib(11) =         89
fib(12) =        144
fib(13) =        233
fib(14) =        377
fib(15) =        610
fib(16) =        987
fib(17) =      1,597
fib(18) =      2,584
fib(19) =      4,181
fib(20) =      6,765

5.3. Le problème du cavalier

Etant donné un échiquier de $n × n$ cases, un cavalier étant placé sur la première case en haut à gauche (ou sur n'importe quelle autre case), peut-on déplacer le cavalier de manière à ce qu'il passe par toutes les cases mais avec la contrainte qu'il ne doit passer par une case qu'une seule fois ?

Le problème du cavalier est un cas particulier des graphes hamiltoniens.

Dans la théorie des graphes, un chemin hamiltonien d'un graphe orienté est un chemin qui passe par tous les sommets une fois et une seule.

On pourra consulter Wikipédia pour plus d'informations.

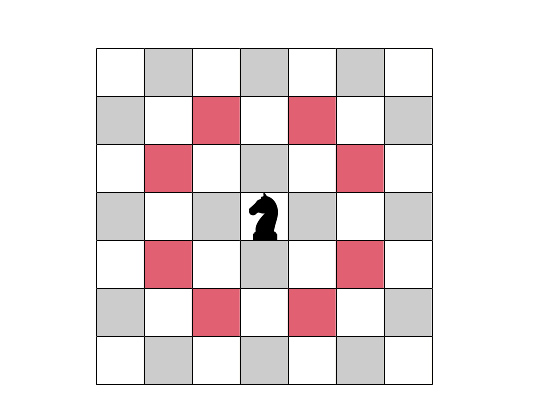
déplacement cavalier
Exemple des 8 déplacements possibles du cavalier

Il s'agit d'un problème combinatoire qui demande beaucoup de calculs car il faut tester tous les cas possibles pour trouver une, voire toutes les solutions. Ce problème est en effet NP-Complet.

5.4. Résolution

5.4.1. Définition des variables

Créez un programme Python nommé cavalier.py.

On commence par définir les variables dont on aura besoin :

  1. // dimension de l'échiquier
  2. dimension est un entier = 5
  3.  
  4. // définition de l'échiquier
  5. échiquier est une matrice entier [dimension, dimension]
  6.  
  7. // nombre de solutions trouvées
  8. nbr_solutions est un entier = 0
  9.  
  10.  
  11. // déplacements du cavalier sur l'axe des x
  12. deplacements_x est un tableau entier = [-1,  1, 2,  2, 1, -1, -2, -2]
  13. // déplacements du cavalier sur l'axe des y
  14. deplacements_y est un tableau entier = [-2, -2, 1, -1, 2,  2, -1, 1]

Initialement chaque case de l'échiquier contiendra la valeur 0 pour indiquer qu'elle n'a pas encore été visitée. Puis au fur et à mesure de la recherche l'échiquier se remplit avec des valeurs positives : 1 représente la première case visitée, puis 2 la seconde, etc, jusqu'à $N^2$ où $N$ est la dimension de l'échiquier.

5.4.2. Algorithme de résolution

On conçoit ensuite l'algorithme de résolution du problème qui est un sous-programme récursif basé sur le retour-arrière (backtrack).

Procédure trouver_toutes_les_solutions(y, x, étape)
Entrée y position en y sur le damier
x position en x sur le damier
etape nième itération
Sortie on ne retourne aucune valeur mais on augmente le nombre de solutions trouvées
Variables
globales
  • l'échiquier
  • deplacements_x : les déplacements suivant l'axe des x du cavalier
  • deplacements_y : les déplacements suivant l'axe des y du cavalier
Variables
locales		 (prochain_y, prochain_x) : prochaine position du cavalier
Description On cherche de manière récursive toutes les solutions en essayant toutes les positions possibles du cavalier (prochain_y, prochain_x). Si le cavalier est à l'intérieur de l'échiquier on continue la recherche .
  1.  
  2. si etape > dimension * dimension alors
  3.   nbr_solutions = nbr_solutions + 1
  4.   print(échiquier)  
  5.  
  6. sinon
  7.   // pour chaque déplacement
  8.   pour i de 1 à taille(deplacement_x) faire
  9.  
  10.     // nouvelles coordonnées du cavalier
  11.     prochain_x est un entier = x + deplacements_x[ i ]
  12.     prochain_y est un entier = y + deplacements_y[ i ]
  13.  
  14.     // si on n'est pas en dehors de l'échiquier
  15.     si position_valide(prochain_y, prochain_x)  alors
  16.  
  17.       // si on n'a pas encore visité la case
  18.       si echiquier[ prochain_y ][ prochain_x ] == 0 alors
  19.  
  20.         echiquier[ prochain_y ][ prochain_x ] = etape
  21.         trouver_toutes_les_solutions(prochain_y, prochain_x, etape + 1)
  22.         echiquier[ prochain_y ][ prochain_x ] = 0
  23.  
  24.       fin si
  25.  
  26.     fin si
  27.  
  28.   fin pour
  29. fin si
  30.  
  31.  

La résolution du problème s'effectue en appelant le sous-programme de résolution en partant de la position (1,1) -- en haut à gauche, soit (0,0) en Python -- et en considérant qu'il s'agit de l'étape 1. Ce qui se traduit par le code suivant :

# placer le cavalier sur le damier en haut à gauche
echiquier[0][0] = 1
# rechercher la prochaine position en partant de (0,0)
trouver_toutes_les_solutions( 0, 0, 2 )

Il faut également écrire la fonction position_valide(y,x) qui vérifie que pour la position $(y,x)$, les coordonnées $x$ et $y$ sont bien dans l'intervalle $[0,dimension-1]$.

Exercice 5.2

Continuer à modifier le programme Python cavalier.py qui résoud ce problème.

  • on commence par créer l'échiquier composé de $n × n$ cases initialisées à 0
  • on écrit ensuite la fonction position_valide(y,x)
  • puis le sous-programme récursif trouver_toutes_les_solutions(y,x,etape)

5.5. Résultats

Exercice 5.3

Testez votre programme avec une taille d'échiquier de $5$. Vous devriez trouver $304$ solutions.

Avec Python le temps de résolution est prohibitif, pour $n=6$ après 7 heures de calcul on a obtenu 167_610 solutions sur les 524_486 existantes.

 n   C++   Python   Amélioration   Solutions 
 5   0,31   11,34   36,58   304 
 6   250   >7h (167610)   ?   524486 
Problème du cavalier, temps d'exécution en secondes sur Intel i7-4790 CPU @ 3.60GHz

Dans la table précédente on a indiqué (colonne Amélioration) le facteur d'amélioration entre C++ et Python (càd le rapport temps_C++ / temps_Python).

5.6. Stratégie de Wansdorff

S'il vous reste du temps, vous pouvez tanter d'implanter une stratégie due à Warnsdorff. Elle consiste à choisir en premier, pour chacun des déplacement du cavalier à une position donnée, les déplacements où le cavalier à le moins de possibilités de déplacement

Le but est d’éviter les cases dites en cul-de-sac pour lesquelles le cavalier réalise de nombreux déplacements inutiles.

il faut pour cela créer une fonction qui va calculer les déplacements valides et évaluer pour chaque déplacement $(y',x')$ le nombre d'autres déplacements possibles. Puis ordonner les déplacements en commençant par ceux qui mènent à des déplacements les plus faibles par la suite.