3. TP - Nombres premiers



3.1. Introduction

Dans ce TP, on s'intéresse aux nombres premiers, à leur identification et leur recherche.

On rappelle la définition d'un nombre premier : il s'agit d'un entier naturel qui possède deux diviseurs distincts : 1 et lui-même.

En conséquence le nombre 1 n'est pas premier car il ne possède qu'un seul diviseur.

La liste des premiers nombres premiers est : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, ...

3.2. Déterminer si un nombre est premier ou non

On désire écrire une fonction en Python qui accepte un argument entier et qui permet de déterminer si un nombre est premier ou non. On renverra True si le nombre est premier, sinon on renverra False

On va par la suite écrire plusieurs versions.

3.2.1. Première version naïve et lente

Dans un premier temps, on détermine si un nombre est premier ou non en comptant son nombre de diviseurs.

Voici l'algorithme de la fonction à implanter :

fonction est_premier(n)
Entrée n (entier) : nombre pour lequel on doit déterminer s'il est premier ou non
Sortie booléen, vrai si n est premier, faux sinon
Variables
locales		 nbr_diviseurs (entier) : compte le nombre de diviseurs de n
Description On calcule le nombre de diviseurs de n,
s'il en existe deux alors le nombre est premier
  1. fonction est_premier(n est un entier) : booléen
  2.  
  3.   // initialement on n'a aucun diviseur
  4.   nbr_diviseurs est un entier = 0
  5.  
  6.  
  7.   // on recherche les diviseurs potentiels
  8.   pour i de 1 à n faire
  9.     si i est_un_diviseur_de n alors
  10.       nbr_diviseurs = nbr_diviseurs + 1
  11.     fin si
  12.   fin pour
  13.  
  14.   // en fonction du nombre de diviseurs on indique
  15.   // si le nombre est premier ou non
  16.   si nbr_diviseurs == 2 alors
  17.     retourner vrai
  18.   sinon
  19.     retourner faux
  20.   fin si
  21.  
  22. fin fonction 
  23.  

La seule difficulté rencontrée consiste à déterminer si $i$ est un diviseur de $n$ :

Pour trouver le reste de la division, on utilise l'opération modulo : $n\ %\ i$

Exercice 3.1

Ecrire le programme nombres_premiers_compte_diviseurs.py qui calcule les nombres premiers entre 1 et $N$ en utilisant la fonction est_premier(n). $N$ est un paramètre qui sera passé au programme. Regarder sous Google comment faire en utilisant le package sys.

En résultat on affichera, la liste des nombres premiers et la somme des nombres de la liste.

python3 python3 nombres_premiers_compte_diviseurs.py 100
 
[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
1,060

Exercice 3.2

Mettre en commentaire l'affichage de la liste des nombres premiers.

Calculez le temps d'exécution pour la recherche des nombres premiers entre 1 et 20000 en utilisant la commande time du shell.

Voici le résultat sur AMD Ryzen 5 5600G :

\$ time python3 nombres_premiers_compte_diviseurs.py 20000
sum = 21,171,186

real	0m5,704s
user	0m5,694s
sys	0m0,008s

3.2.2. Deuxième version améliorée et efficace

La version précédente n'est pas efficace pour plusieurs raisons :

Prenons un exemple ($n = 37$) pour comprendre pourquoi il ne faut pas aller au-delà de $√(37)+1$

 diviseurs   quotient   reste 
 1   37   0 
 2   18   1 
 3   12   1 
 4   9   1 
 5   7   2 
 6   6   1 
 7   5   2 
 8   4   5 
 9   4   1 
 10   3   7 
 etc   etc   etc 
Recherche des diviseurs de 37

Au-delà de 7 les quotients seront nomarlement inférieurs à 7, or on a déjà testé les diviseurs de 1 à 7.

Voici l'algorithme de la fonction est_premier basée sur le calcul du nombre de divisieurs.

Fonction est_premier(n)
Entrée n (entier) : nombre pour lequel on doit déterminer s'il est premier ou non
Sortie booléen, vrai si n est premier, faux sinon
Description On cherche les diviseurs impairs de 3 à $√(n)+1$
  1. fonction est_premier(n est un entier) : booléen
  2.  
  3.   i est un entier
  4.  
  5.   si n <= 1 alors
  6.     retourner faux
  7.   sinon si 2 <= n et n <= 3 alors
  8.     retourner vrai
  9.   sinon si n est_disible_par 2 alors
  10.     retourner faux
  11.   sinon
  12.     // rechercher des diviseurs
  13.     pour i de 3 à sqrt(n)+1 par pas de 2 faire
  14.       si n est_divisible_par i alors
  15.         retourne faux
  16.       fin si
  17.     fin pour
  18.   fin si
  19.  
  20.   // aucun diviseur trouvé, le nombre est premier
  21.   retourner vrai
  22.  
  23. fin fonction 
  24.  

L'implantation en Python pose un seul problème lié à la racine carrée car elle fait partie des calculs sur les nombres réels :

Exercice 3.3

Ecrire le programme nombres_premiers_efficace.py qui calcule les nombres premiers entre 1 et $N$ en utilisant la nouvelle fonction est_premier(n).

Tout comme dans le programme précédent, en résultat on affichera la somme des nombres de la liste.

Exercice 3.4

Calculez le temps d'exécution pour la recherche des nombres premiers entre 1 et 20000 en utilisant la commande time du shell.

Que remarquez vous ?

<

3.2.3. Crible d'Erathostène

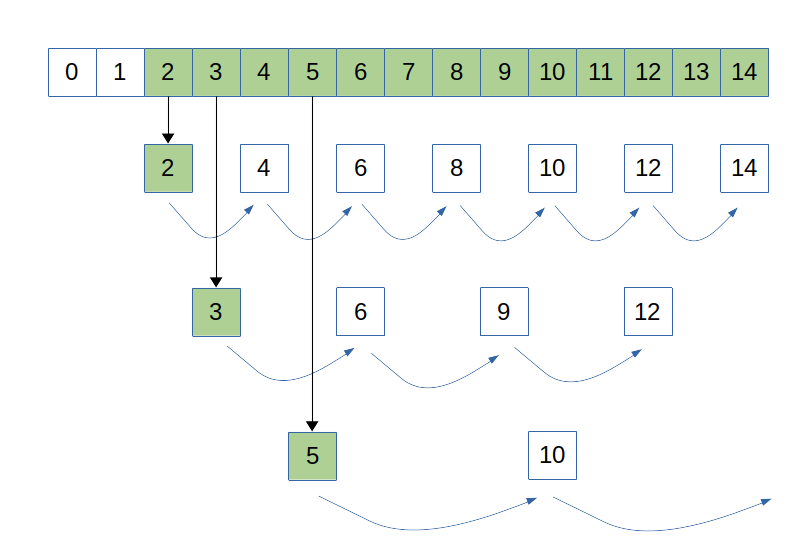
Une autre solution, plutôt que de déterminer si un nombre $n$ est premier, consiste à utiliser un tableau de booléens tableau_nombres_premiers où chaque tableau_nombres_premiers[i] est vrai si $i$ est un nombre premier.

Pour remplir le tableau, on procède ainsi :

Crible

fonction
Description remplir un tableau et éliminer les multiples
  1. // créer et remplir le tableau
  2. // si on recherche les 3000 premiers nombres premiers
  3. // il faut prend maximum = 27449
  4. variable t est un tableau de [1 à maximum] booléens
  5.  
  6. pour i de 2 à maximum faire
  7.   t[i] = vrai
  8. fin pour
  9.  
  10. t[0] = faux
  11. t[1] = faux
  12.  
  13. // éliminer les multiples
  14. pour i de 2 à maximum faire
  15.   si t[i] == vrai alors
  16.     pour j de 2*i à maximum par pas de i faire
  17.       t[j] = faux
  18.     fin pour
  19.   fin si
  20. fin pour
  21.  
  22. // créer et retourner la liste des nombres premiers
  23. variable l est une liste entiers = vide
  24.  
  25. pour i de 1 à maximum faire
  26.   si t[i] == vrai alors
  27.     ajouter i à l
  28.   fin si
  29. fin pour
  30.  
  31. retourner l
  32.  

Exercice 3.5

Ecrire le programme nombres_premiers_crible.py qui calcule les nombres premiers entre 1 et $N$ en utilisant la méthode du crible.

Tout comme dans le programme précédent, en résultat on affichera la somme des nombres de la liste.

Exercice 3.6

Calculez le temps d'exécution pour la recherche des nombres premiers entre 1 et 20000 en utilisant la commande time du shell.

3.3. Conjecture de Collatz

S'il vous reste du temps...

On appelle suite de Collatz (Lothar Collatz), une suite de nombres générée par la fonction de Collatz appliquée récursivement à partir d'un entier naturel $n$.

La fonction de Collatz est une fonction récursive applicable à tout entier positif $n$, définie par :

  • si $n$ est pair, alors $n=n/2$
  • si $n$ est impair, alors $n = 3n+1$

La conjecture de Collatz, ou conjecture de Syracuse, énonce qu'une suite de Collatz se termine par $1$.

Exercice 3.7

Ecrire le programme collatz.py qui permet de le vérifier pour tout $n$. On s'arrêtera dès que $n = 1$.

On testera pour $n = 27$.

[27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1]

Cette suite comporte 112 termes.

Attention, il faut utiliser la division entière : //.