5. Algorithmique 4 - Tris

5.1. Rappels

Voici un tableau récapitulatif des complexités des méthodes de tri :

 Méthode de tri   Complexité temporelle
(pire des cas) 		  Complexité temporelle
(en moyenne) 		  Complexité temporelle
(meilleur des cas) 
 Tri à bulles   $O(n^2)$   $O(n^2)$   $O(n)$ 
 Tri par sélection   $O(n^2)$   $O(n^2)$   $O(n^2)$ 
 Tri par insertion   $O(n^2)$   $O(n^2)$   $O(n)$ 
 Tri rapide (Quicksort)   $O(n^2)$   $O(n×log(n))$   $O(n×log(n))$ 
 Tri fusion (Mergesort)   $O(n×log(n))$   $O(n×log(n))$   $O(n×log(n))$ 
 Tri par tas (Heapsort)   $O(n×log(n))$   $O(n×log(n))$   $O(n×log(n))$ 
Evolution du tri par insertion

On distingue donc les méthodes en

Nous allons étudier quatre méthodes de tris :

5.2. Le tri par insertion

On l'appelle également tri du joueur de cartes. Il consiste à chaque étape à replacer l'élément t[i] dans le tableau trié t[1:i-1].

 i   j   1   2   3   4   5 
 ?   ?   25   24   23   22   21 
 2   2   24   25   23   22   21 
 3   3   24   23   25   22   21 
 3   2   23   24   25   22   21 
 4   4   23   24   22   25   21 
 4   3   23   22   24   25   21 
 4   2   22   23   24   25   21 
 5   5   22   23   24   21   25 
 ...   ...   ...   ...   ...   ...   ... 
Evolution du tri par insertion
  1. proc insertion_sort( t is array[1..n] of int ) {
  2.  
  3.     for i in 2..n do
  4.         var j = i
  5.    
  6.         while ((j > 0) and (t[ j ] < t[ j - 1 ])) do
  7.             swap( t[ j - 1 ], t[ j ] )
  8.             j = j - 1
  9.         end while
  10.        
  11.     end for
  12.    
  13. end proc
  14.  
  15.  

L'intérêt du tri par insertion et qu'il est généralement rapide sur des tableaux de petite taille, c'est à dire d'une vingtaine d'éléments.

Si le tableau est déjà trié, la complexité sera de $O(n)$.

Dans le cas général, la complexité est en $O(n^2)$.

Exercice 5.1

Essayez d'exécuter le tri par insertion sur le tableau suivant : [1, 7, 4, 3, 6, 8, 2].

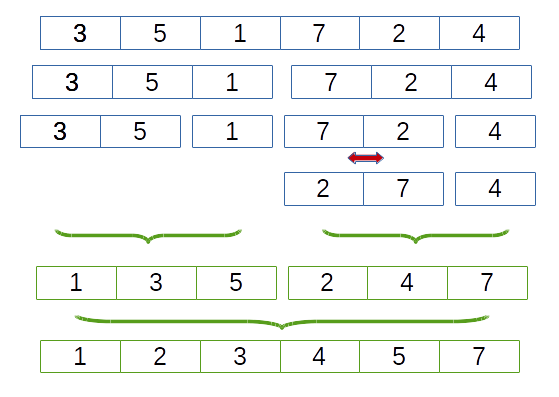
5.3. Le tri fusion

Le tri fusion consiste :

merge sort

  1. // ------------------------------------------------------------------
  2. //
  3. //  What:
  4. //
  5. //      Main function that performs merge_sort
  6. //
  7. // Parameters:
  8. //
  9. //      t an array of integers
  10. //
  11. // ------------------------------------------------------------------
  12. proc merge_sort( t is array[1..n] of int )
  13.  
  14.     // start recursive split
  15.     split(t, 1, n)
  16.    
  17. end proc
  18.  
  19. // ==================================================================
  20. //
  21. //  What:
  22. //
  23. //      Recursively split the initial array in two subarrays
  24. //
  25. // Parameters:
  26. //
  27. //      a is the minimum index of array t
  28. //      b is the maximum index of array t
  29. //
  30. // ==================================================================
  31. proc split( t is array[1..n] of int; a, b  are int )
  32.  
  33.     var size = b - a + 1
  34.    
  35.     if size = 1 then
  36.    
  37.         exit proc
  38.        
  39.     if size = 2 then
  40.    
  41.         if t[a] > t[a+1] then
  42.             swap( t[a], t[a+1] )
  43.         end if
  44.        
  45.     else
  46.         // m is the middle index
  47.         var m = (a + b + 1) / 2
  48.         split( t, a, m-1 )
  49.         split( t, m, b )
  50.         merge( t, a, m, b )
  51.     end if
  52.    
  53. end proc
  54.  
  55. // ==================================================================
  56. //
  57. //  What:
  58. //
  59. //      Merge two subarrays into a one array and copy result to
  60. //      the initial array
  61. //
  62. //  Parameters:
  63. //
  64. //      t an array of integers
  65. //      a is the minimum index of array t
  66. //      m is the middle index of array t
  67. //      b is the maximum index of array t
  68. // 
  69. // ==================================================================
  70. proc merge( t is array[1..n] of int; a, m, b are int ) {
  71.  
  72.     // array which is the result of the merge of arrays
  73.     // from [a..m] and [m+1..b]
  74.     var tmp is array[1..b-a+1] of int
  75.     var i = a
  76.     var j = m
  77.    
  78.     // copy back data following order into tmp
  79.     while (i < m) and(j < b+1) do
  80.         if t[i] < t[j] then
  81.             tmp[k] = t[i]
  82.             i = i + 1
  83.             k = k + 1
  84.         else if t[j] < t[i] then
  85.             tmp[k] = t[j]
  86.             j = j + 1
  87.             k = k + 1
  88.         else
  89.             tmp[k] = t[i]
  90.             i = i + 1
  91.             k = k + 1
  92.             tmp[k] = t[j]
  93.             j = j + 1
  94.             k = k + 1
  95.         end if
  96.     end while
  97.  
  98.     while i < m do
  99.         tmp[k] = t[i]
  100.         i = i + 1
  101.         k = k + 1
  102.     end while
  103.  
  104.     while j < b+1 do
  105.         tmp[k] = t[i2]
  106.         j = j + 1
  107.         k = k + 1
  108.     end while
  109.  
  110.     // copy tmp to t[a]
  111.     t[a..b] = tmp[1..t.size()]
  112.    
  113. end proc
  114.  
  115.  

Exercice 5.2

Essayez d'exécuter le tri fusion sur le tableau suivant : [1, 7, 4, 3, 6, 8, 2].

5.4. Le tri rapide

Il s'agit d'une méthode de type divide and conquer (diviser pour régner). En informatique, diviser pour régner est une méthode de conception d'algorithmes réduisant récursivement un problème en un ou plusieurs sous-problèmes du même type qui sont indépendants.

Le principe du tri rapide consiste à réaliser une partition des éléments du sous-tableau [p..r] par rapport à une valeur pivot notée $x$ que l'on placera à un indice $q$ du tableau de telle sorte que :

On espère ainsi que statistiquement $q$ sera proche de $(p+r)/2$, donc placé au milieu du tableau.

On trie ensuite récursivement le sous-tableau gauche et le sous-tableau droit (cf. animation).

Pour que le tri soit le plus rapide possible il faudrait choisir à chaque fois une valeur pivot qui scinde le tableau initial en deux parties égales, ce qui n'est pas possible à moins d'examiner les valeurs à trier mais cela reviendrait à perdre du temps.

L'algorithme est le suivant :

  1. proc _quick_sort( t is array[1..n] of int; a, b are int)
  2.  
  3.     if a < b then
  4.    
  5.         // pivot in the middle of the array
  6.         var m = (b + a + 1) / 2
  7.         var x = t[ m ]
  8.        
  9.         swap( t[ m ], t[ b ] )
  10.  
  11.         var q = a
  12.         for i in a..b-1 do
  13.            
  14.             if t[ i ] < x then
  15.                 swap( t[ i ], t [q++ ])
  16.             end if 
  17.            
  18.         end for
  19.        
  20.         swap( t[ b ], t[ q ] )
  21.                
  22.         if (a < q) _quick_sort( t, a, q - 1 )
  23.         if (q < b) _quick_sort( t, q + 1, b )
  24.        
  25.     end if
  26.    
  27. end proc
  28.  
  29.  
  30.  
  31. proc quick_sort( t is array[1..n] of int )
  32.  
  33.     _quick_sort( t, 1, n )
  34.  
  35. end proc
  36.  
  37.  

Exercice 5.3

Essayez d'exécuter le tri rapide sur le tableau suivant : [1, 7, 4, 3, 6, 8, 2].

5.5. Le tri rapide aidé du tri par insertion

On reprend le même algorithme que pour le tri rapide, cependant lorsque le tableau à trier possède une taille inférieure ou égale à 15 éléments (voire jusqu'à 20 ou 24), on utilise le tri par insertion car on sait que celui-ci sera généralement plus rapide comme le montre le graphique suivant :

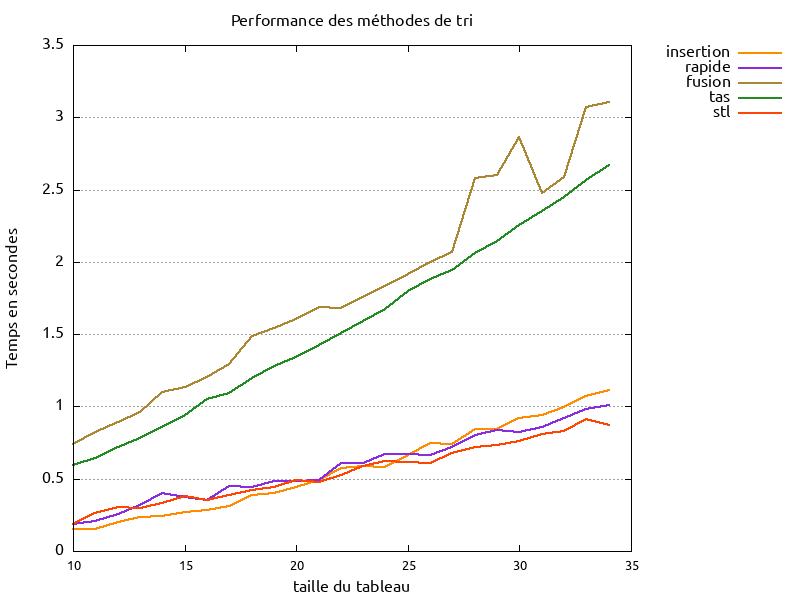
Tris petite taille de tableau
Temps sur AMD Ryzen 5 5600G pour 10 millions de tris du même tableau

Un rapide test, pour des tailles de tableaux de 15 ou 25 éléments, montre que le tri par insertion :

 Méthode   Taille   Comparaisons   Swaps   Total   Ratio 
 tri rapide   15   182.70   16.60   199.30   4.91 
 tri insertion   15   119.00   54.30   173.30   0.77 
 tri rapide   18   226.70   21.40   248.10   4.77 
 tri insertion   18   170.00   75.20   245.20   0.76 
 tri rapide   20   252.20   23.40   275.60   4.6 
 tri insertion   20   209.00   87.40   296.40   0.74 
 tri rapide   25   330.30   30.20   360.50   4.48 
 tri insertion   25   324.00   139.70   463.70   0.74 
Nombre de comparaisons et swaps en moyenne pour 10 exécutions sur des données aléatoires

Ici le ratio représente le nombre total d'opérations (comparaisons + swaps) divisé par la complexité de la méthode dans le pire des cas.

Pour le tri rapide, le facteur multiplicatif diminue progressivement à mesure que la taille du tableau augmente :

  • il est de $4,91$ pour $n=15$
  • de $3,44$ pour $n=10^5$
  • de $3,38$ pour $n=10^6$
  • de $3,3$ pour $n=10^7$

Dernier point : sur le graphique précédent le tri rapide est plus performant que le tri par insertion à partir de 25 éléments et non pas 20 comme le montre la complexité. Cela est dû à l'implantation du code. La méthode du tri rapide est récursive et les appels de fonctions ne sont pas pris en compte dans le calcul de la complexité. Ces appels récursifs influent sur le temps de calcul.

  1. // tri rapide avec insertion
  2.  
  3. proc _quick_insertion_sort( t is array[1..n] of int; a, b are int)
  4.  
  5.     if (b - a) > 15 then
  6.         if a < b then
  7.        
  8.             // pivot in the middle of the array
  9.             var m = (b + a + 1) / 2
  10.             var x = t[ m ]
  11.            
  12.             swap( t[ m ], t[ b ] )
  13.  
  14.             var q = a
  15.             for i in a..b-1 do
  16.                
  17.                 if t[ i ] < x then
  18.                     swap( t[ i ], t [q++ ])
  19.                 end if 
  20.                
  21.             end for
  22.            
  23.             swap( t[ b ], t[ q ] )
  24.                    
  25.             if (a < q) _quick_insertion_sort( t, a, q - 1 )
  26.             if (q < b) _quick_insertion_sort( t, q + 1, b )
  27.  
  28.     else
  29.        
  30.         insertion_sort( t,  a , b );
  31.                
  32.     end if
  33.    
  34. end proc
  35.  
  36.  
  37.  
  38. proc quick_insertion_sort( t is array[1..n] of int )
  39.  
  40.     _quick_insertion_sort( t, 1, n )
  41.  
  42. end proc
  43.  
  44.  

5.6. Code source

Le code source pour Linux est disponible ici. Il a été compilé avec gcc 10.3 sans générer d'erreur ou de warning.

Pour compiler, exécuter : make dans le terminal.

Pour lancer le script de tests lancer : ./test_tris.sh

5.7. Résultats

Voici quelques résultats de performance. On reporte le temps d'exécution moyen pour 10 exécutions pour différentes méthodes de tri pour des tableaux remplis par des valeurs aléatoires.

 Méthode   Taille   Temps(s) 
 insertion   15   0.000001 
 fusion   15   0.000003 
 rapide   15   0.000001 
 rapide + insertion   15   0.000000 
 insertion   100   0.000019 
 fusion   100   0.000009 
 rapide   100   0.000007 
 rapide + insertion   100   0.000005 
 insertion   1k   0.000979 
 fusion   1k   0.000089 
 rapide   1k   0.000052 
 rapide + insertion   1k   0.000042 
 insertion   10k   0.064443 
 fusion   10k   0.000814 
 rapide   10k   0.000523 
 rapide + insertion   10k   0.000557 
 insertion   100k   6.217739 
 fusion   100k   0.009813 
 rapide   100k   0.007587 
 rapide + insertion   100k   0.005696 
 insertion   1m   573.051 
 fusion   1m   0.085273 
 rapide   1m   0.056630 
 rapide + insertion   1m   0.054368 
 fusion   10m   0.965430 
 rapide   10m   0.642476 
 rapide + insertion   10m   0.599273 
 fusion   100m   10.831880 
 rapide   100m   7.275618 
 rapide + insertion   100m   6.9855 
 fusion   1M   121.696 
 rapide   1M   82.441 
 rapide + insertion   1M   78.947 
Temps en secondes pour trier des tableaux d'entiers de différentes tailles sur AMD Ryzen 5600 G

Dans le tableau précédent :

On remarque donc que :

5.8. Autres améliorations (ChatGPT)

L'implémentation la plus efficace du tri rapide (Quicksort) repose sur plusieurs améliorations et optimisations. Certaines des améliorations notables sont :

  1. Choisir un pivot efficace : Choisir un bon pivot est crucial pour assurer une bonne performance du tri rapide. Une approche courante pour choisir un pivot efficace consiste à utiliser la "médiane de trois", qui sélectionne le pivot comme étant la médiane des trois éléments (premier, milieu et dernier éléments). Cette méthode réduit la probabilité de tomber sur le pire des cas.
  2. Insertion sort pour les petits tableaux : Lorsque la taille du sous-tableau à trier devient suffisamment petite, le tri par insertion est généralement plus rapide que le tri rapide. Par conséquent, on peut utiliser le tri par insertion pour les petits sous-tableaux, en définissant un seuil (par exemple, 10 à 20 éléments).
  3. Utiliser une approche "introspective" : L'introsort est une variante du tri rapide qui combine le tri rapide, le tri par insertion et le tri par tas. L'idée est de commencer par le tri rapide et de passer au tri par tas si la profondeur de récursion dépasse une certaine limite (généralement basée sur la taille du tableau). Le tri par insertion est utilisé pour les petits sous-tableaux, comme mentionné précédemment.
  4. Tri rapide en parallèle : Le tri rapide peut être parallélisé pour tirer parti des architectures multi-cœurs. Plusieurs implémentations parallèles existent, comme le "parallel Quicksort" qui divise les sous-tableaux en parallèle.

En résumé, l'implémentation la plus efficace du tri rapide dépend de plusieurs facteurs, tels que la méthode de sélection du pivot, l'utilisation d'autres algorithmes de tri pour des cas spécifiques et la parallélisation pour tirer parti des ressources matérielles disponibles. La méthode de Hoare ou de Lomuto pour la partition ne fait pas une différence significative en termes d'efficacité globale.