3. Algorithmique 4 - Complexité

3.1. Qu'est-ce la complexité en informatique ?

La complexité en informatique permet de définir la difficulté de résolution d'un problème.

Elle se définit en fonction du nombres d'opérations élémentaires à réaliser sur un traitement (complexité en temps).

Il existe également la complexité en espace qui définit la taille occupée par les données pour un problème donné.

3.1.1. Exemple simple

Par exemple, quelle est la complexité du calcul de la moyenne de $n$ notes stockées dans un tableau ?

Le code C correspondant est le suivant :

  1. /**
  2.  * Calcule la moyenne de n notes
  3.  */
  4. float moyenne( float *tab, int n ) {
  5.  
  6.   float somme = 0;
  7.   for (int i = 0; i < n; ++i) {
  8.     somme += tab[ i ];
  9.   }
  10.  
  11.   float moy = somme / n;
  12.  
  13.   return moy;
  14.  
  15. }
  16.  

On réalise $n$ additions et une division. Si on considère que l'opération élémentaire est une opération arithmétique alors il y a $n+1$ opérations élémentaires : $n$ additions et 1 division.

On dira donc que la complexité du calcul de la moyenne de $n$ notes est de $n$ car quand $n$ est grand, 1 est négligeable.

3.1.1.a  Que compter ?

Si on désirait être exhaustif, il faudrait compter le nombre d'affectations, additions, divisions et de comparaisons : dans la boucle for par exemple, on a :

Celles-ci ne sont généralement pas prises en compte car on considère la boucle for en ligne 7 comme un moyen d'exprimer le fait qu'on va répéter $n$ fois : somme += tab[i].

3.1.1.b  Temps de calcul

Normalement le temps d'exécution d'un algorithme est proportionnel à sa complexité. Cependant, il faut faire attention, car certaines simplifications gomment les aspects liés à l'exécution des instructions par le microprocesseur. En effet une comparaison ou une addition prennent moins de temps à s'exécuter qu'une multiplication. Réaliser une division, calculer un sinus, un logarithme sont des opérations coûteuses en nombre de cycles d'exécution.

3.1.2. Notation $O()$

Pour introduire une complexité, on utilise la notation $O(x)$ ou $x$ est une expression en fonction des données à traiter. Cette notation a été introduite par Paul Bachmann (1837-1920), mathématicien allemand, puis reprise par Edmund Landau (1877-1938), également mathématicien allemand. $O(x)$ signifie proportionnel à $x$ :

$∃α ∈ ℕ$, alors $O(αx)$ se notera $O(x)$.

Comme on vient de le voir, calculer la moyenne de $n$ nombres est un traitement qui possède une compexité en $O(n)$.

Voici, présentés dans le tableau ci-dessous, quelques ordres de grandeur de la complexité :

 Expression   Exemple 
 $O(1)$   lire une valeur dans un tableau en fonction de son indice 
 $O(n/2)$ ou $O(n)$   rechercher une valeur dans une liste de valeurs 
 $O(n × log(n))$   trier un tableau de données avec une méthode efficace (quick sort) 
 $O(n^2)$   trier un tableau de données avec une méthode pas très efficace (bubble sort) 
 $O(n^3)$   faire le produit de deux matrices carrées de dimension $n$ 
 $O(n!)$   maximum de parcimonie en bioinformatique 
 $O(e^n)$   les échecs 
Exemples de compléxités


Le petit utilitaire qui suit permet de voir l'évolution d'un sous ensemble de courbes liées à la complexité.

CANVAS NOT SUPPORTED IN THIS BROWSER!

▬▬▬▬
▬▬▬▬
▬▬▬▬
▬▬▬▬
▬▬▬▬
▬▬▬▬
▬▬▬▬


n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
log2(n) 0
n * log(n) 0
n^2 1
n^3 1
2^n 2
n! 1

Examinez ce qui se passe lorsqu'on compare $4.7 × n × log(n)$ à $0.75 × n^2$.



Exercice 3.1

Quelle est la complexité en temps du calcul sur 15 niveaux des situations de jeu aux échecs si on considère que l'on peut jouer en moyenne 20 coups ?

Quel temps d'exécution sera nécessaire sur une seule machine pour calculer toutes les situations de jeu sachant qu'on peut évaluer une situation en 1 nanoseconde ?

Exercice 3.2

Quelle est la complexité spatiale dans les mêmes conditions que précédemment ?

3.2. Complexités dans le pire et le meilleur des cas

Suivant les algorithmes et les données qu'ils traitent il n'est pas toujours possible de donner une complexité qui couvre tous les cas possibles. On pourra alors essayer de borner la complexité en donnant :

la complexité moyenne est généralement la moyenne de la complexité dans le pire et le meilleur des cas.

3.2.1. Exemple de la recherche dans un tableau non trié

Quelle est la complexité de la recherche d'une valeur entière $x$ dans un tableau non trié de $n$ entiers ?

Le code C de cette recherche est par exemple :

  1. /**
  2.  * Recherche d'un élément x dans un tableau non trié
  3.  * On retourne l'indice de l'objet dans le tableau ou
  4.  * -1 si l'élément n'est pas dans le tableau
  5.  */
  6. int recherche( int *tab, int n, int x ) {
  7.  
  8.   for (int i = 0; i < n; ++i) {
  9.     if ( tab[ i ] == x ) return i;
  10.   }
  11.  
  12.   // non trouvé
  13.   return -1;
  14.  
  15. }
  16.  

L'opération élémentaire est ici la comparaison de $x$ avec un élément du tableau.

La complexité moyenne est donc :

$$ O( {n+1}/2 ) ≈ O( n/2 ) $$

On pourra alors soit prendre $O(n/2)$, soit $O(n)$.

3.2.2. Exemple de la recherche dans un tableau trié

Quelle est la complexité de la recherche d'une valeur entière $x$ dans un tableau trié de $n$ entiers ?

On peut comme précédemment utiliser une recherche séquentielle qui parcourt le tableau en passant de l'indice $i$ à l'indice $i+1$. Ou alors, on peut utiliser une recherche plus efficace qui est la recherche dichotomique :

  1. #include <iostream>
  2. using namespace std;
  3.  
  4. int recherche_dichotomique( int *tab, int lo, int hi, int x ) {
  5.  
  6.   if (lo > hi) return -1;
  7.  
  8.   int m = (lo + hi) / 2; 
  9.   if ( tab[ m ] == x ) return m;
  10.   if ( x < tab[ m ] ) {
  11.     return recherche_dichotomique( tab, lo, m-1, x );
  12.   } else {
  13.     return recherche_dichotomique( tab, m+1, hi, x );
  14.   }
  15.  
  16. }
  17.  
  18. /**
  19.  * Recherche d'un élément x dans un tableau non trié
  20.  * On retourne l'indice de l'objet dans le tableau ou
  21.  * -1 si l'élément n'est pas dans le tableau
  22.  */
  23. int recherche( int *tab, int n, int x ) {
  24.  
  25.   return recherche_dichotomique( tab, 0, n, x );
  26.  
  27. }
  28.  
  29. int main() {
  30.   int tab[10] = { 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 };
  31.  
  32.   for (int i = -1; i < 22; ++i) {
  33.     cout << i << ": " << recherche( tab , 10, i ) << endl;
  34.   }
  35.  
  36.   return EXIT_SUCCESS;
  37. }
  38. /
  39. int recherche_dichotomique( int *tab, int lo, int hi, int x ) {
  40.  
  41.   if (lo > hi) return -1;
  42.  
  43.   int m = (lo + hi) / 2; 
  44.   if ( tab[ m ] == x ) return m;
  45.   if ( x < tab[ m ] ) {
  46.     return recherche_dichotomique( tab, lo, m-1, x );
  47.   } else {
  48.     return recherche_dichotomique( tab, m+1, hi, x );
  49.   }
  50.  
  51. }
  52.  
  53. /**
  54.  * Recherche d'un élément x dans un tableau non trié
  55.  * On retourne l'indice de l'objet dans le tableau ou
  56.  * -1 si l'élément n'est pas dans le tableau
  57.  */
  58. int recherche( int *tab, int n, int x ) {
  59.  
  60.   return recherche_dichotomique( tab, 0, n, x );
  61.  
  62. }
  63.  
  64. int main() {
  65.   int tab[10] = { 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 };
  66.  
  67.   for (int i = -1; i < 22; ++i) {
  68.     cout << i << ": " << recherche( tab , 10, i ) << endl;
  69.   }
  70.  
  71.   return EXIT_SUCCESS;
  72. }
  73.  

La recherche dichotomique consiste à chaque étape à prendre l'élément au milieu du sous-tableau puis à éliminer la partie supérieure ou inférieure du tableau en fonction de $x$ et de la valeur au milieu du tableau en faisant varier les bornes inférieure ou supérieure de la zone de recherche.

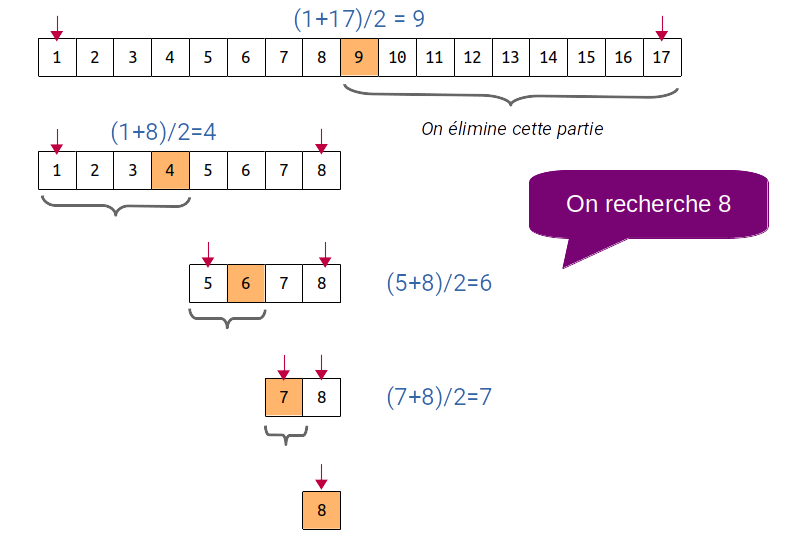
recherche dichotomique

On aura donc si $n = 2^k$, $k$ comparaisons à réaliser. Dès lors :

$$ n = 2^k \,\,⇒\,\, \text"ln"(n) = k × \text"ln"(2) \,\,⇒\,\, k = {\text"ln"(n)}/{\text"ln"(2)} \,\,⇒\,\, k = \text"log"_2(n) $$

La complexité de la recherche dichotomique est donc $O(log_2(n))$.

3.3. Exercices

Exercice 3.3

On rappelle que $log_2(n) = {ln(n)}/{ln(2)}$ et donc $log_2(2^n) = {ln(2^n)}/{ln(2)} = n × {ln(2)}/{ln(2)} = n$.

On suppose qu'une méthode de recherche ($R_1$) dans un ensemble de valeurs est de complexité $O(n × √{n} × log_2(n))$.

On peut utiliser une autre méthode de recherche ($R_2$) mais dans ce cas il faut extraire et trier par ordre croissant les valeurs de l'ensemble puis ensuite rechercher de manière dichotomique la valeur. L'opération d'extraction est en $O(n^2)$ et ne sera réalisée qu'une seule fois. Pour rappel, la recherche dichotomique possède une complexité en $O(log_2(n))$.

  • si le nombre de valeurs de l'ensemble est $n = 1024$, combien d'opérations faut-il pour effectuer une recherche suivant $R_1$ ? Même question pour $R_2$, détaillez vos calculs.
  • toujours avec $n = 1024$, à partir de quelle valeur de $k$, $k$ étant le nombre de recherches, la recherche suivant $R_1$ devient-elle moins intéressante qu'avec $R_2$ ?