CUDA : cours travaux pratiques

Sommaire

Warning: include(cuda_td_summary.php): failed to open stream: No such file or directory in /home/jeanmichel.richer/public_html/cuda_mp_reduction.php on line 16

Warning: include(): Failed opening 'cuda_td_summary.php' for inclusion (include_path='.:/usr/share/php') in /home/jeanmichel.richer/public_html/cuda_mp_reduction.php on line 16

6. TD Réduction

6.1. Introduction

L'algorithme de réduction est un algorithme important en parallèlisme.

6.1.1. Réduction - définition

On considère un tableau de $n$ éléments et un opérateur associatif et commutatif $⊕$ doté d'un élément neutre $I$. A partir du tableau

$$ [ a_0, a_1, ..., a_{n-1} ] $$

on désire obtenir un unique résultat :

$$ a_0 ⊕ a_1 ⊕ ... ⊕ a_{n-1} $$

Si $⊕$ est l'addition alors la réduction permet d'obtenir la somme des éléments du tableau.

On peut appliquer cet algorithme avec d'autres opérateurs comme la multiplication, minimum, maximum.

Pour que l'algorithme soit parallélisable efficacement il suffit que l'opérateur $⊕$ soit associatif et commutatif :

commutativité : $a ⊕ b = b ⊕ a$
associativité : $a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c$

6.2. Version séquentielle

Une version séquentielle est donnée par le code EZ language suivant : on calcule la somme.

function reduction(input is array of integer) return integer
begin
	sum is integer = 0
	
	for i in input.range() do
		sum = sum + input[i];
	end for
	
	return sum
end function

Voici une version plus élaborée : on utilise la STL et les template afin de simplifier l'écriture du code.

On utilise un tableau avec les données en entrée input.

CODE
sequential_reduction.cpp

// compile with g++ -std=c++11 -Wall -O2
#include <iostream>
#include <iterator>
#include <algorithm>
#include <cstdlib>
#include <cmath>
#include <cstring>
using namespace std;
 
/**
 * print array
 */
template<class T>
void print_array(string s, T *a, int size) {
    cout << s;
    copy(&a[0], &a[size-1], ostream_iterator<T>(cout, ", "));
    cout << a[size-1];
    cout << endl;
}
 
/**
 * functor for addition
 */
template<class T>
class PlusOperator {
public:
    static T operation(T a, T b) {
        return a + b;
    }
    
    static T identity() {
        return 0;
    }
};
 
/**
 * functor for product
 */
template<class T>
class ProductOperator {
public:
    static T operation(T a, T b) {
        return a * b;
    }
    
    static T identity() {
        return 1;
    }
};
 
/**
 * Reduction with functor as template parameter
 * @param in  input array
 * @param size number of elements of the array
 */
template<class T, class Oper>
T reduction(T *input, int size) {
    // set first output element as first input element
    T result = Oper::identity();
    for (int i=0; i<size; ++i) {
        result = Oper::operation(result, input[i]);
    }
    return result;
}
 
 
/**
 * main function
 */
int main(int argc, char *argv[]) {
    int MAX_ELEMENTS = 16;
    int *int_input;
    double *dbl_input;
    int start = 1;
    int int_result;
    double dbl_result;
    
    if (argc > 1) {
        MAX_ELEMENTS = atoi(argv[1]);
    }
    
    // allocate input and output arrays
    int_input = new int [ MAX_ELEMENTS ];
    dbl_input = new double [ MAX_ELEMENTS ];
    
    // fill int_input array with 1, 2, 3, ....
    generate(&int_input[0], &int_input[MAX_ELEMENTS], [&start]() {
        return start++; 
    });
 
    // fill dbl_input
    start = 1;
    generate(&dbl_input[0], &dbl_input[MAX_ELEMENTS], [&start]() {
        return start++; 
    });
 
    // print input values
    print_array<int>("input array of integers : ", int_input, MAX_ELEMENTS);
    print_array<double>("input array of integers : ", dbl_input, MAX_ELEMENTS);
    
    // reduction with integer and +
    int_result = reduction<int, PlusOperator<int>>(int_input, MAX_ELEMENTS);
    cout << "result with + : " << int_result << endl;
    // reduction with double and *
    dbl_result = reduction<double, ProductOperator<double>>(dbl_input, MAX_ELEMENTS);
    cout << "result with * : " << fixed << dbl_result << endl;
    
    delete [] int_input;
    delete [] dbl_input;
    
    return EXIT_SUCCESS; 
}
 
 

./code_reduction_seq.exe 10
input array of integers : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
input array of integers : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
result with + : 55
result with * : 3628800.000000

La complexité de cet algorithme est en $O(n)$, ou $n$ est la taille du tableau.

6.3. Versions parallèles

6.3.1. le coeur de l'algorithme

On peut écrire une version qui fonctionne comme la version séquentielle mais en utilisant une addition atomique :

function parallel_reduction(input is array of integer) return integer
begin
	sum is integer = 0
	meta parallel
	for i in input.range() do
		sum = atomic_add(sum, input[i]);
	end for 
	return sum
end function

La fonction atomic_add est bloquante et seul un thread peut l'exécuter à la fois. On obtient au final un traitement séquentiel, ce qui n'est pas intéressant du point de vue de la performance et nous fait perdre l'utilité du parallèlisme.

L'algorithme dans sa version parallèle efficace utilise une décomposition arborescente du tableau.

Voici un exemple avec l'addition :

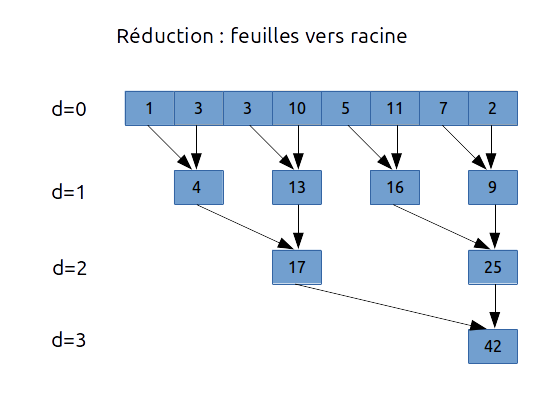
Reduction

Ainsi la complexité est en $O(\log_2(n))$ : on effectue toujours $n-1$ additions mais en $\log_2(n)$ étapes. Dans le cas présent :

pour le niveau $d = 1$, on a 4 additions effectuées en parallèles
pour le niveau $d = 2$, on a 2 additions effectuées en parallèles
pour le niveau $d = 3$, on a 1 addition

6.3.1.a version 0

L'algorithme peut être écrit sous la forme suivante. On considère un tableau input composé de $n$ éléments, le premier élement du tableau étant input[0] et le dernier input[n-1].

On considère ici que $n$ est une puissance de 2 supérieure ou égale à 1024.

On utilise une grille 1D de blocs de 256 threads par exemple de manière à avoir au moins 4 blocs (puisque $n ≧ 1024)$.

On parcourt le tableau de deux en deux, puis de quatre en quatre, ..., grâce à la variable stride que l'on peut traduire en français par foulée ou enjambée.

CODE
reduction_v0_1.cpp

/**
 * kernel to perform reduction of array used as
 * input and output
 */
__global__ void reduction_v0(T *input, int size) {
    // we use a grid 1D of blocks 1D
    // Global thread Index
    int i = blockIdx.x * blockDim.x + threadIdx.x;
 
    // perform reduction in GPU global memory
    for (int stride = 1; stride < size; stride *= 2) {
        if (((i + 1) % (2*stride)) == 0) {
            input[i] += input[i - stride];
        }
        __syncthreads();
    }
}
 
// call to kernel
// consider that size = 128
dim3 block_dim(64, 1, 1);
dim3 grid_dim(2, 1, 1);
reduction_v0<<<grid_dim, block_dim>>>(gpu_input, size);
 
 

1, 2, 3,  4, 5,  6, 7,  8  
1, 3, 3,  7, 5, 11, 7, 15
1, 3, 3, 10, 5, 11, 7, 26
1, 3, 3, 10, 5, 11, 7, 36

On peut modifier le code pour obtenir une autre version qui commence avec les indices pairs:

CODE
reduction_v0_2.cpp

/**
 * kernel to perform reduction of array used as
 * input and output
 */
__global__ void reduction_v0(T *input, int size) {
    // we use a grid 1D of blocks 1D
    // Global thread Index
    int i = blockIdx.x * blockDim.x + threadIdx.x;
 
    // perform reduction in GPU global memory
    for (int stride = 1; stride < size; stride *= 2) {
        if ((i % (2*stride)) == 0) {
            input[i] += input[i + stride];
        }
        __syncthreads();
    }
}
 
// call to kernel
// consider that size = 128
dim3 block_dim(64, 1, 1);
dim3 grid_dim(2, 1, 1);
reduction_v0<<<grid_dim, block_dim>>>(gpu_input, size);
 
 

 1, 2, 3, 4,  5, 6,  7, 8
 3, 2, 7, 4, 11, 6, 15, 8
10, 2, 7, 4, 26, 6, 15, 8
36, 2, 7, 4, 26, 6, 15, 8

Analyse

on modifie les données en entrée : on pourrait vouloir les garder intactes
on travaille en mémoire globale du GPU : input[i] += input[i - stride]; ce qui n'est pas très performant
problème majeur : cela ne fonctionne pas ! En effet sous GTX 560 Ti avec un tableau initial composé de '1' et l'opérateur +, l'algorithme dans sa version v0_2 semble fonctionner jusqu'à size=8192, mais donne 8193 pour size=16384 alors qu'on devrait obtenir 16384.

Cela est du au fait qu'il n'y a pas de synchronisation des écritures en mémoire globale du GPU en fonction des blocs.

Si on prend l'algorithme dans sa version v0_1 alors cela fonctionne jusqu'à size=32768 mais à partir de size=65536 on obtient parfois le résultat escompté et parfois un résultat différent (61440 par exemple)
l'instruction __syncthreads() permet uniquement de synchroniser les threads d'un bloc, mais il n'existe pas d'instruction de synchronisation de tous les blocs ou entre les blocs.
l'explication du non fonctionnement est la suivante (Forum NVidia) :

I am to use elementary numbers, to make it easier; the principle applies nevertheless. You are using device x, with y sm's, with the constraints and conditions of device x's compute capability you wish to scan/reduce 2000 elements your device can only seat 10 blocks of 100 threads each, at a time, meaning 1000 elements

input[i] += input[i + stride]

when thread i gets to a stride that would imply i + stride = 1500, it expects element 1500 is ready but element 1500 can not be ready; in fact, element 1001 to 2000 would not be ready and so the reduction/scan breaks down, because of a violation of its premises

Améliorations

calculer une somme partielle pour chaque bloc et stocker les résultats dans un autre tableau
charger les données en mémoire partagée et travailler en mémoire partagée : accélération des traitements et synchronisation des données/threads

6.3.1.b version 1

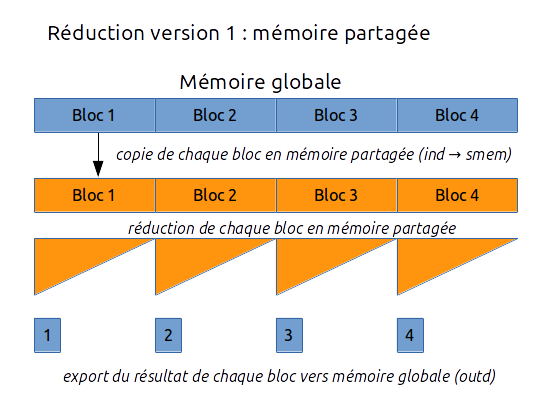
Le principe de la version 1 est le suivant :

on copie les blocs de la mémoire globale vers la mémoire partagée de chaque bloc
on effectue la réduction sur chaque bloc
on copie le résultat dans la mémoire globale
puis on recommence pour le bloc 1 qui finalise le calcul

Réduction version 1

CODE
reduction_v1.cpp

/**
 * reduction 
 * @param input array of input data
 * @param output partial sum of each block
 * @param size number of elements of ind
 */
__global__ void reduction_v1(int *input, int *output, int size) {
    // local thread index
    int ltid = threadIdx.x;
    // global thread index
    int gtid = blockIdx.x * blockDim.x + threadIdx.x;
 
    extern __shared__ int smem[];
    
    // load data in shared memory
    smem[ltid] = (i < size) ? input[gtid] : 0;
    __syncthreads();
 
    // perform reduction in shared memory
    for (int stride = 1; stride < blockDim.x; stride *= 2) {
        // modulo is slow
        if (ltid % (2*stride) == 0) {
            smem[tid] += smem[ltid + stride];
        }
        __syncthreads();
    }
    
    // write result for this block to global output memory
    if (tid == 0) {
        output[blockIdx.x] = smem[0];
    }
}
 
// consider that size = 128
dim3 block_dim(64, 1, 1);
dim3 grid_dim(2, 1, 1);
// amount of shared memory used
int smem_size = block.x * sizeof(int)
// gpu_output
cudaMalloc((void **)&gpu_output, grid.x*sizeof(int));
// call kernel
reduction_v1<<<grid_dim, block_dim, smem_size>>>(gpu_input, gpu_output, size);
 
 

Reste un dernier problème : comment faire la somme des éléments du tableau output ?

Plusieurs solutions peuvent être proposées :

faire la somme sur le CPU en utilisant l'algorithme accumulate de la STL par exemple
relancer la réduction de output sur le GPU en relançant la fonction de réduction avec output passé en paramètre de input, mais dans ce cas il faut utiliser un deuxième tableau output2 pour stocker le résultat
toujours sur le GPU, faire en sorte que le thread de GTID 0 fasse la somme à la fin du kernel de réduction

6.4. Travail

Implantez les algorithmes de réduction en CUDA et tester la performance de ces algorithmes pour différentes tailles de tableaux :

utilisation d'opérations atomiques
utilisation de la version 1 avec calcul du résultat sur GPU
solution tout GPU avec deux appels successifs du kernel (utiliser __syncthreads())
solution tout GPU avec le dernier thread qui réalise la somme (utiliser __syncthreads() ) puis __threadfence() avant de faire la somme

__threadfence() is used to halt the current thread until all previous writes to shared and global memory are visible by other threads.

6.5. Bibliographie et sitographie

Optimizing Parallel Reduction in CUDA par Mark Harris, NVidia

Page de Jean-Michel Richer