Ce site est en cours de reconstruction certains liens peuvent ne pas fonctionner ou certaines images peuvent ne pas s'afficher.
11.1. Linear Regression
Consider three series of data that we want to compare, we want to know if the data of $x$ are related to $y$ or $z$ via a linear relationship.
> x <- c(10,20,30,40,50) > y <- c(105, 210, 302, 415, 506) > z <- c(10,60,80,40,25)
By plotting y and z in function of $x$ we can see that there exists a linear relationship between $x$ and $y$ but not between $x$ and $z$.
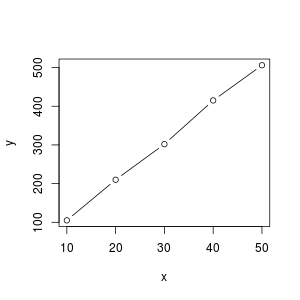
y = f(x), linear
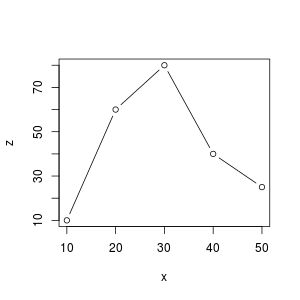
z = f(x), parabola
In order to confirm the linear relationship between $x$ and $y$ we could use the cor() function or R.
The correlation coefficient of two variables in a data set equals to their covariance divided by the product of their individual standard deviations. It is a normalized measurement of how the two are linearly related.
If the correlation coefficient is close to 1, it would indicate that the variables are positively linearly related
> cor(x,y) # x and y are strongly related (value close to 1.0) [1] 0.9995255 > cor(x,z) [1] 0.05698029 # x and z are not related linearly (value close to 0.0)
Simple linear regression
Let us determine if $x$ is related to $y$, by performing a linear regression that will try to find a formula to predict $x$ from $y$ of the form $x' = c_0 + c_1 × y + ε$, where $ε$ is some residual error:
lm is used to fit linear models. It can be used to carry out regression, single stratum analysis of variance and analysis of covariance (although ‘aov’ may provide a more convenient interface for these).
> x <- c(10,20,30,40,50)
> y <- c(105, 210, 302, 415, 506)
> z <- c(60, 16, 1, 18, 64)
# apply linear regression
> fit <- lm(y ~ x)
> summary(fit)
/*
Call:
lm(formula = y ~ x)
Residuals:
1 2 3 4 5
-1.2 3.1 -5.6 6.7 -3.0
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 5.5000 5.9422 0.926 0.423
x 10.0700 0.1792 56.205 1.24e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 5.666 on 3 degrees of freedom
Multiple R-squared: 0.9991, Adjusted R-squared: 0.9987
F-statistic: 3159 on 1 and 3 DF, p-value: 1.241e-05
*/
> fit$fitted.values
1 2 3 4 5
106.2 206.9 307.6 408.3 509.0
From the previous calculation we see that the p-value is close to 0 (1.241e-05) and the $R^2$ value is close to 1.0 (0.9991 ) which means that the data are correlated by a linear relation.
The p-value helps you determine the significance of your results, it is a probability (between 0 and 1.0) that the difference observed between data is due to randomness. In other words:
- if the p-value is less than a threshold $α$ (generally 5%), so if $p < α = 0.05$, it is said that you reject the null hypothesis $H_0$, in plain language terms the null hypothesis is usually an hypothesis of no difference, so you accept the alternative hypothesis $H_1$ which is the opposite of the null hypothesis
- if $p > α$ then you can consider that the data are not related
By obtaining the coefficients (see below) we can determine that $y = 5.50 + 10.07 * x$.
> c = coefficients(fit)
> c
(Intercept) x
5.50 10.07
# define function f
> f <- function(x) {
+ return (5.50 + 10.07 * x)
+ }
# apply function f to each element of x
> estimated_y = sapply(x, f)
> estimated_y
[1] 106.2 206.9 307.6 408.3 509.0
> abs(estimated_y - y)
[1] 9.8 14.1 5.4 17.7 8.0
> abs(estimated_y - y)/y
[1] 0.011428571 0.014761905 0.018543046 0.016144578 0.005928854
Finally the formula $f$ gives use values close to the ones of $x$.
For example for the first value $x=10$ we have $y=105$ and the estimated value of $y$ using $f(x)$ is 106.2, so this is a difference of $|106.2-105| = 1.2$ but only a 1.1% difference in the estimation.
If you apply the same reasoning between $z$ and $x$ then you will find:
> fit <- lm(z ~ x)
> summary(fit)
/*
Call:
lm(formula = z ~ x)
Residuals:
1 2 3 4 5
30.2 -14.8 -30.8 -14.8 30.2
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 28.800 34.312 0.839 0.463
x 0.100 1.034 0.097 0.929
Residual standard error: 32.71 on 3 degrees of freedom
Multiple R-squared: 0.003105, Adjusted R-squared: -0.3292
F-statistic: 0.009343 on 1 and 3 DF, p-value: 0.9291
*/
Here the p-value is greater than 0.05 (0.9291) and $R^2$ is far from 1.0 (0.003105), so the data are not related by a linear function.
Multiple linear regression
Consider the following set of data (hwas.RData) that concerns 45 persons for which we have:
- the height in cm
- the weight in kg
- the age in years
- the sex: M(ale) or F(emale)
> mydata <- read.table("hwas.RData", header=T)
> head(mydata)
height.cm weight.kg age.years sex
1 171 66 43 M
2 179 76 75 M
3 170 70 64 M
4 177 73 44 M
5 164 64 76 M
6 158 48 84 M
> tail(mydata)
height.cm weight.kg age.years sex
40 169 60 53 F
41 142 47 41 F
42 132 40 73 F
43 179 71 44 F
44 158 56 54 F
45 160 58 49 F
The question we want to answer is: is there a relationship between the weight of a person and its height, age and sex ?
For this we will try to establish a linear regression with multiple variables called a Multiple Linear Regression. In this example the sex is a qualitative variable and must be transformed into a factor.
We are looking for a formula of the form:
$$weight = c_0 + c_1 × height + c_2 × age + c_3 × factor(sex)$$
> fit <- lm(weight.kg ~ height.cm + age.years + factor(sex), mydata)
> summary(fit)
/*
Call:
lm(formula = weight.kg ~ height.cm + age.years + factor(sex),
data = mydata)
Residuals:
Min 1Q Median 3Q Max
-8.9930 -2.3789 0.0152 2.4916 10.6506
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -49.79115 7.18988 -6.925 2.1e-08 ***
height.cm 0.67519 0.03940 17.138 < 2e-16 ***
age.years -0.03552 0.03597 -0.988 0.3291
factor(sex)M 3.08788 1.20561 2.561 0.0142 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.899 on 41 degrees of freedom
Multiple R-squared: 0.8933, Adjusted R-squared: 0.8855
F-statistic: 114.4 on 3 and 41 DF, p-value: < 2.2e-16
*/
The summary of the model tells us that
- $c_0 = -49.79$ and $c_1 = 0.67$ have high significance
- the sex has a relatively low significance
- the age has no significance
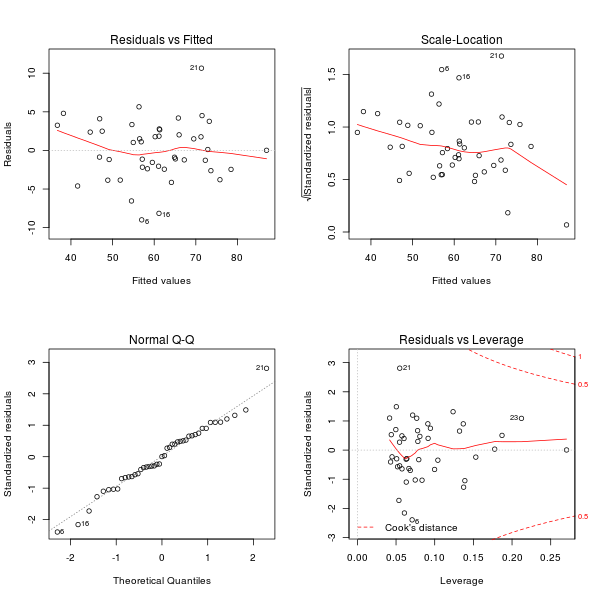
We can obtain more information by plotting the fit:
png("plot_mlr.png", width=600, height=600)
layout(matrix(c(1,2,3,4),2,2))
plot(fit)
dev.off()
We can see that the rows 6, 16 and 21 are special cases that could be eliminated to get a better quality of the results. Indeed if you compute the following:
> abs(mydata$weight.kg - fitted(fit)) / mydata$weight.kg
1 2 3 4 5 6
0.0185895122 0.0593196479 0.0599180243 0.0240749166 0.0417450186 0.1873539680
7 8 9 10 11 12
0.0001746786 0.0856648324 0.0202647057 0.1244780636 0.0192085184 0.0137794968
13 14 15 16 17 18
0.0434182144 0.0285949603 0.0323257050 0.1537868846 0.0424802727 0.0267483668
19 20 21 22 23 24
0.0910796105 0.0296565849 0.1298858838 0.0369519727 0.0489174598 0.0187958505
25 26 27 28 29 30
0.0394608419 0.1116779434 0.0803081176 0.0577353400 0.0245524695 0.0347036671
31 32 33 34 35 36
0.1363442466 0.0498313711 0.0527068355 0.0016231839 0.0800729522 0.0293002426
37 38 39 40 41 42
0.0171666004 0.0689881522 0.0179873810 0.0405570195 0.0504353766 0.0814775486
43 44 45
0.0210558261 0.0183786203 0.0258828757
You can see that the estimation compared to the real value have for:
- for item 6, a difference of 18.73%
- for item 16, a difference of 15.37%
- for item 21, a difference of 12.98%
If we remove those rows we could get a more accurate prediction:
Warning: Undefined variable $weight in /home/jeanmichel.richer/public_html/r_lr.php on line 422
Warning: Undefined variable $weight in /home/jeanmichel.richer/public_html/r_lr.php on line 422
# remove rows 6, 16 and 21 don't forget the ',' at the end
> mydata <- mydata[ -c(6,16,21), ]
> fit <- lm(weight.kg ~ height.cm + age.years + factor(sex), mydata)
> summary(fit)
/*
Call:
lm(formula = weight.kg ~ height.cm + age.years + factor(sex),
data = mydata)
Residuals:
Min 1Q Median 3Q Max
-6.7751 -2.1153 0.0418 2.1985 5.1966
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -49.052178 5.609898 -8.744 1.24e-10 ***
height.cm 0.660163 0.030770 21.455 < 2e-16 ***
age.years -0.007251 0.028596 -0.254 0.80119
factor(sex)M 3.334148 0.954162 3.494 0.00122 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 3.022 on 38 degrees of freedom
Multiple R-squared: 0.9328, Adjusted R-squared: 0.9275
F-statistic: 175.8 on 3 and 38 DF, p-value: < 2.2e-16
*/
> sort(abs(mydata.kg - fitted(fit)) / mydata.kg)
34 14 37 1 39 7
0.001967183 0.003663395 0.011945637 0.013001642 0.013740261 0.017049186
11 44 12 24 9 20
0.018756076 0.020320199 0.020855313 0.022422828 0.026523095 0.028207040
4 30 45 43 29 5
0.029974826 0.030568475 0.030712876 0.031013854 0.031270727 0.031286479
15 22 23 36 40 18
0.033585688 0.033622933 0.034386588 0.034519136 0.035518640 0.035654057
32 33 25 28 13 2
0.037691907 0.038652727 0.045318996 0.046220846 0.047950935 0.053850411
41 3 17 42 38 27
0.055452709 0.056490516 0.059040199 0.060998981 0.067439092 0.069220703
35 19 26 8 31 10
0.075250248 0.083816526 0.095299486 0.100601652 0.141146898 0.157403217
11.1.1. Multiple non linear regression
nls determines the nonlinear (weighted) least-squares estimates of the parameters of a nonlinear model
If you want to use nls() you need to provide a formula, so you already have an idea of what you are looking for.
Suppose you have the following data:
> x [1] 10 20 30 40 50 > z [1] 60 16 1 18 64
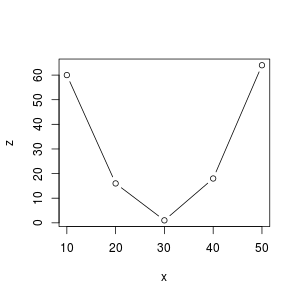
In this case the curve $z=f(x)$ looks like a parabola. So we will try to find a parabola of the form:
$$ a + b × (x - c)^2 $$ or $$ a'x^2 + b'x + c' $$
but we don't know the values of constants $a$, $b$ and $c$, so we need to provide values from where to start to the nls() function:
> fit <- nls(z ~ a*x^2+b*x+c, start=list(a=-100, b=-100,c=-100))
> summary(fit)
/*
Formula: z ~ a * x^2 + b * x + c
Parameters:
Estimate Std. Error t value Pr(>|t|)
a 0.151429 0.001355 111.7 8.01e-05 ***
b -8.985714 0.082882 -108.4 8.51e-05 ***
c 134.800000 1.087592 123.9 6.51e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.5071 on 2 degrees of freedom
Number of iterations to convergence: 1
Achieved convergence tolerance: 8.132e-09
*/
> coefficients(fit)
a b c
0.1514286 -8.9857143 134.8000000
> f <- function(x) 0.1514286*x^2-8.9857143*x+134.8
> sapply(x,f)
[1] 60.085717 15.657154 1.514311 17.657188 64.085785
> estimated_z <- sapply(x, f)
> estimated_z
[1] 60.085717 15.657154 1.514311 17.657188 64.085785
> abs(estimated_z - z)/z
[1] 0.001428617 0.021427875 0.514311000 0.019045111 0.001340391