| Enseignements en L3 Mention informatique |
 |
 |
 |
 |
 |
 |
On considère l'implémentation suivante :
- matrix_int.h (version HTML)
- matrix_int.cpp (version HTML)
- matrix_flt.h
- matrix_flt.cpp
On distingue plusieurs types de méthodes réalisant le produit de 2 matrices :
- basic : il s'agit de l'implémentation directe de la formule mathématique
- basic_inv_jk : implémentation utilisant l'inversion des boucles j et k
- block_32 : produit par blocs de 32 (tuilage 32 × 32)
- block_48 : produit par blocs de 48 (tuilage 48 × 48)
- block_64 : produit par blocs de 64 (tuilage 64 × 64)
- blas_sgemm : utilisation de la librairie BLAS et de la méthode sgemm spécialement dédiée au calcul matriciel pour les float
Voici quelques résultats obtenus sur :
- Intel Core 2 Duo E6420 - 2.13 Ghz - 4 Mo L2 - FSB 1066 Mhz - 3 Go DDR2-SDRAM PC2-5400
- Intel Core 2 Duo E6750 - overclocké à 3 Ghz - FSB 1500 Mhz - 2 Go DDR2-SDRAM PC2-7200 (900 Mhz)
| Integer 3000x3000 | |||
| method | e6420 | e6750 | amélioration |
| gcc - basic | 410 / 391 | 292 / 277 | - / - |
| gcc - basic_inv_jk | 222 / 248 | 158 / 177 | -45% / -36 % |
| gcc - block_32 | 45 / 40 | 32 / 28 | -89% / -89 % |
| gcc - block_48 | 45 / 38 | 31 / 27 | -89% / -90 % |
| gcc - block_64 | 43 / 37 | 30 / 26 | -89% / -90 % |
| Float 3000x3000 | |||
| method | e6420 | e6750 | amélioration |
| gcc - basic | 190 / 366 | 134 / | - / - |
| gcc - basic_inv_jk | 43 / 198 | 31 / 141 | -77% / - % |
| gcc - block_32 | 35 / 28 | 25 / 20 | -81% / - % |
| gcc - block_48 | 35 / 27 | 24 / 19 | -81% / - % |
| gcc - block_64 | 33 / 26 | 23 / 18 | -82% / - % |
| gcc - blas_sgemm | 5 / 5 | 3 / 3 | -97% / - % |
| Double 3000x3000 | |||
| method | e6420 | e6750 | amélioration |
| gcc - basic | 254 / 385 | 167 / 273 | - / - |
| gcc - basic_inv_jk | 58 / 211 | 40 / 148 | -77%/ -45% |
| gcc - block_32 | 37 / 25 | 26 / 17 | -85% / -93% |
| gcc - block_48 | 36 / 23 | 25 / 16 | -85% / -94% |
| gcc - block_64 | 35 / 27 | 25 / 19 | -86% / -93% |
| gcc - blas_dgemm | 10 / 10 | 7 / 7 | -96% / -97 |
Dans les graphiques suivants, les méthodes correspondent à :
- method 0 : implémentation de base (basic)
- method 4 : inversion des boucles (basic_inv_jk)
- method 5 : par bloc de 32x32 (block_32)
- method 6 : par bloc de 64x64 (block_64)
- method 7 : BLAS (blas_sgemm) pour float et double
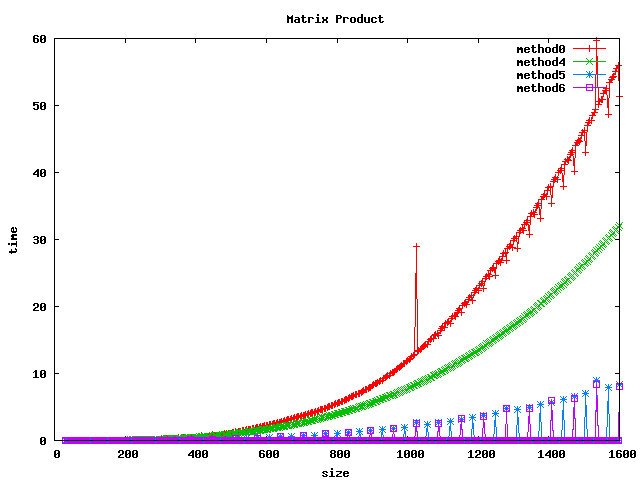
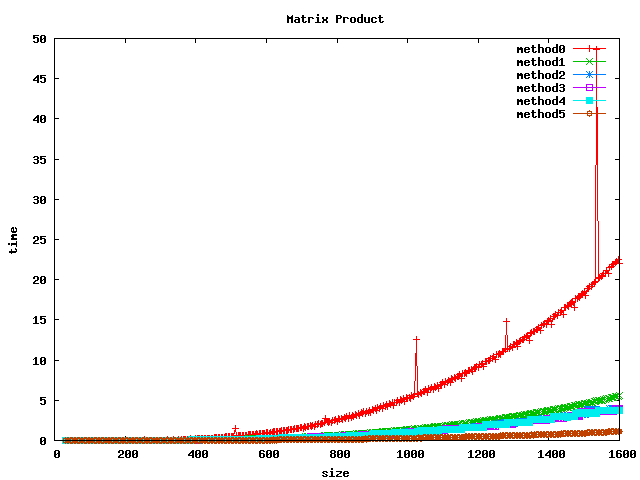
Résultat sur des int
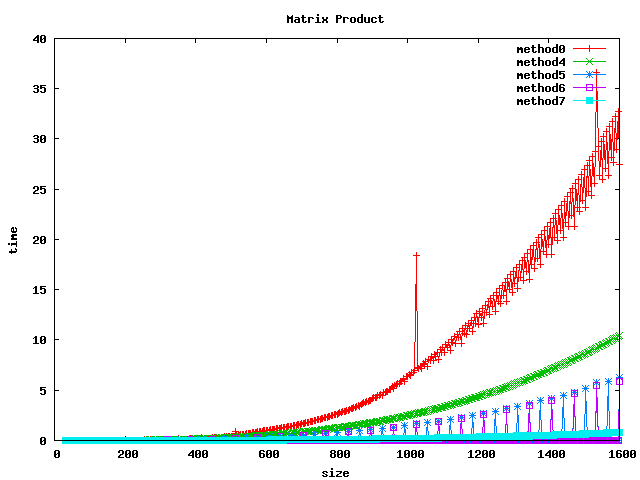
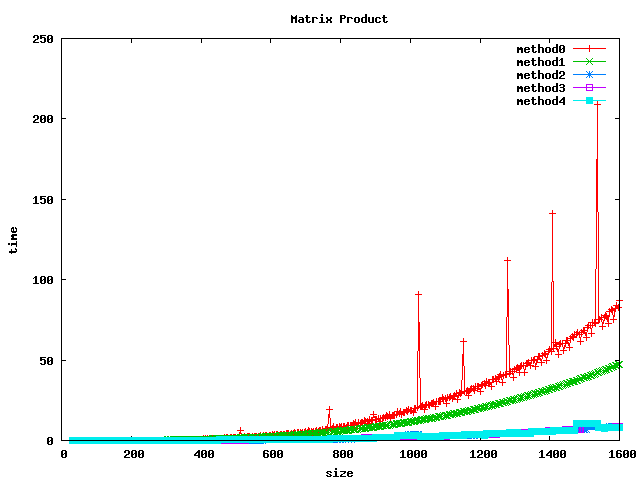
Résultat sur des float
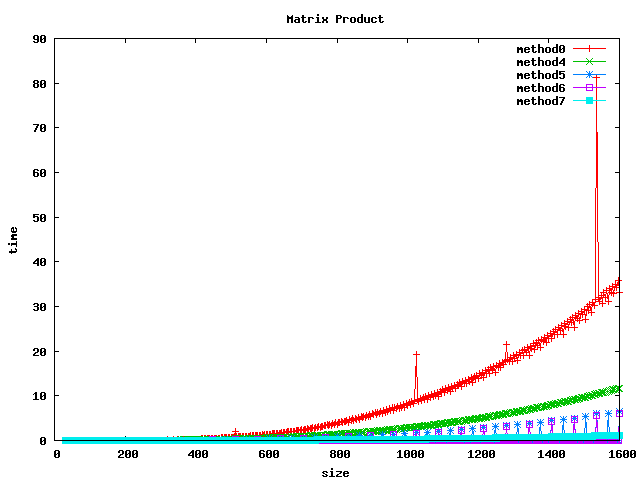
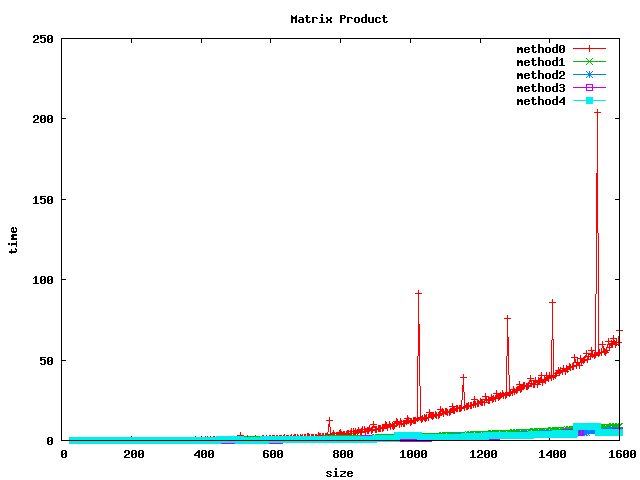
Résultat sur des double
(1) On peut noter, pour le produit basic, un décrochage (temps de calcul plus long) pour certaines dimensions de matrices :
- pour int et float : 1024, 1536
- pour double : 512, 1024, 1280, 1536
| Dimension | Type | Taille (décimal) | Taille (hexadécimal) |
| 1024 | int | 4.194.304 | 400.000 |
| 1536 | int | 9.437.184 | 900.000 |
| 512 | double | 262.144 | 40.000 |
| 1024 | double | 8.388.608 | 800.000 |
| 1024 | double | 13.107.200 | C80.000 |
| 1536 | double | 18.874.368 | 1.200.000 |
(2) L'inversion de boucle (jk) a tendance a diviser le temps de calcul par 2 sur les int et par un facteur 4 à 5 sur les float et double.
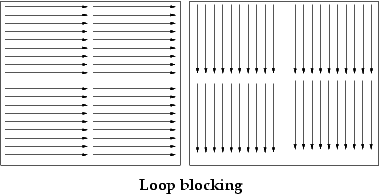
(3) le calcul par bloc (loop blocking) donne de bons résultats.
(4) la librairie BLAS et les fonctions associées sgemm et dgemm donnent les meilleurs résultats.
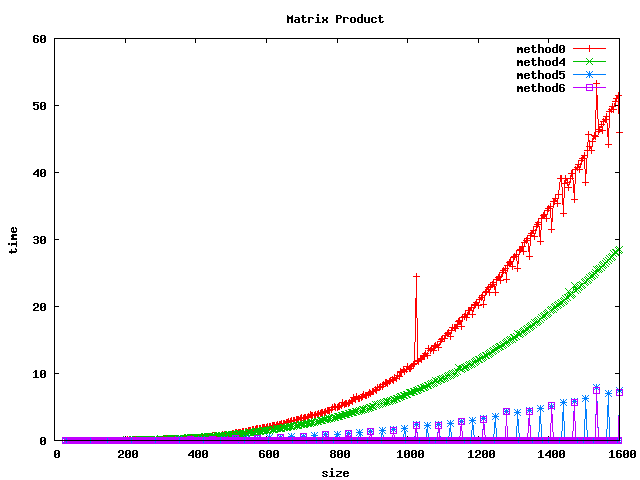
Résultat sur des int
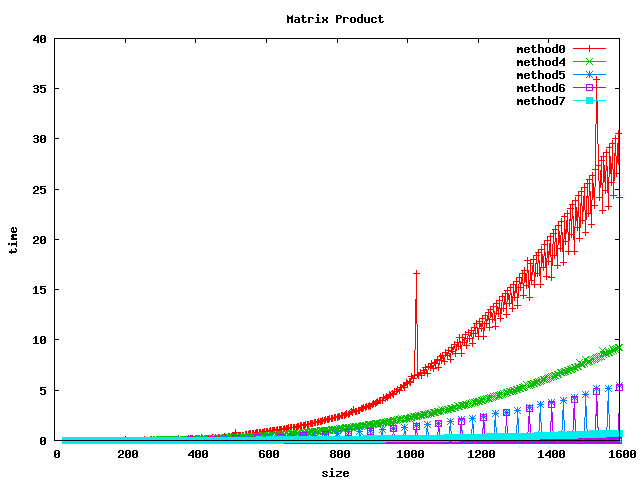
Résultat sur des float
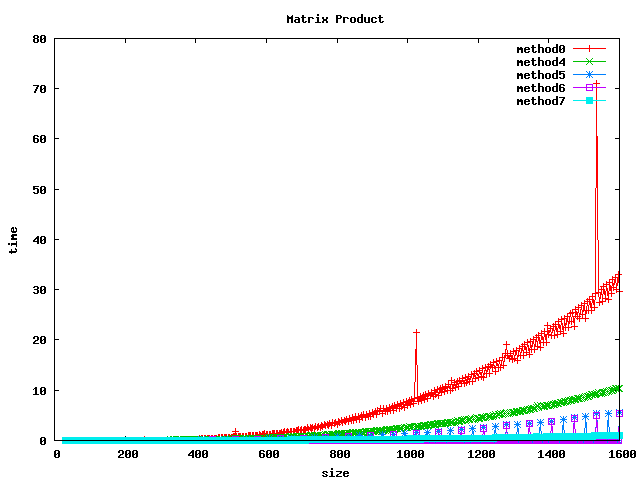
Résultat sur des double
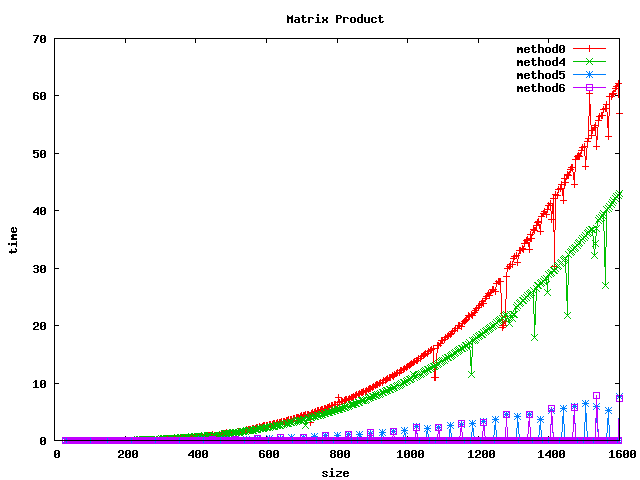
Résultat sur des int
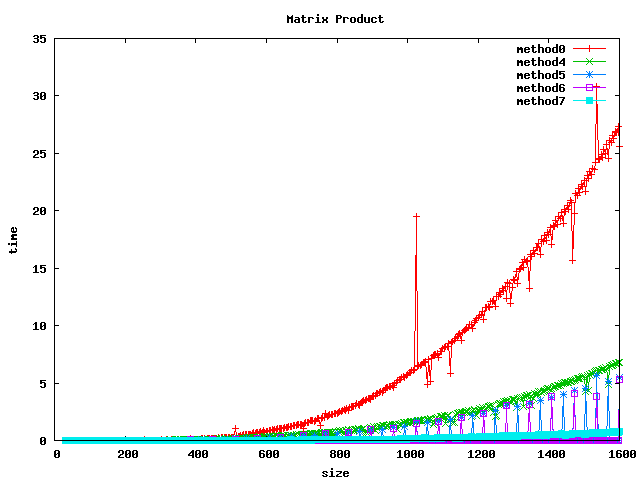
Résultat sur des float
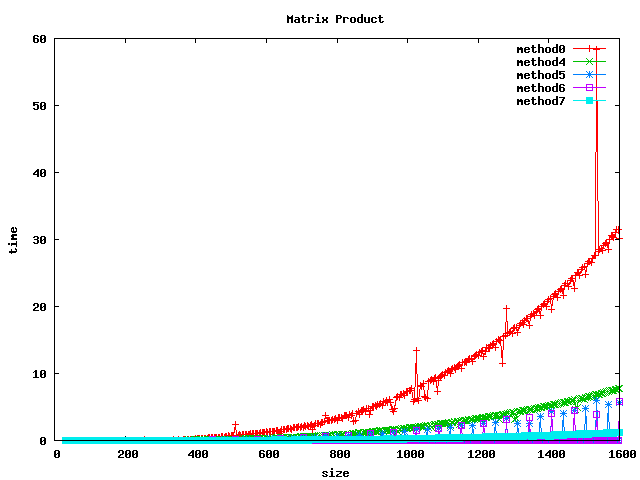
Résultat sur des double
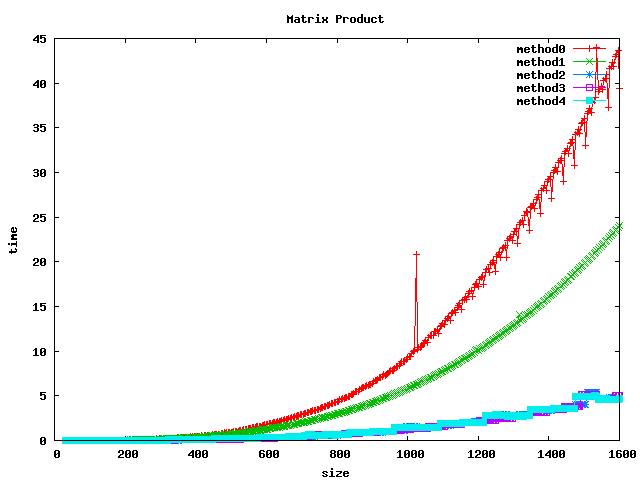
Résultat sur des int
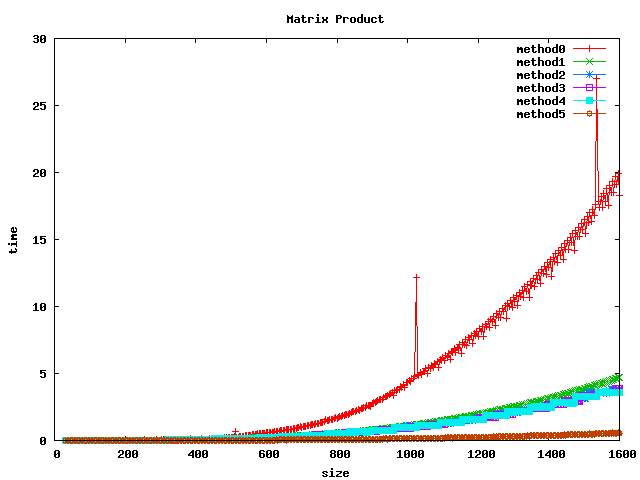
Résultat sur des float
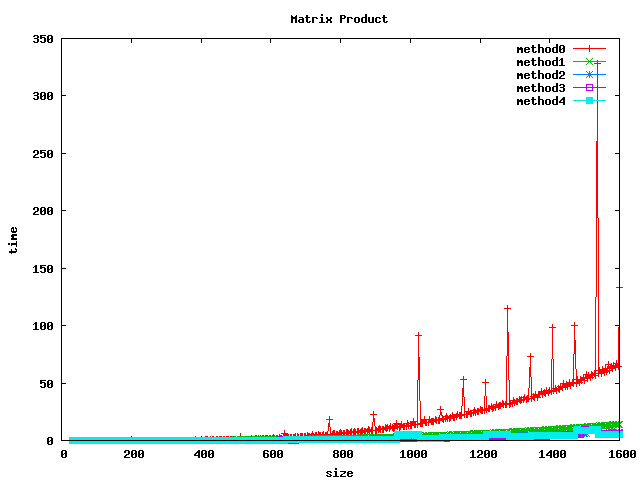
Résultat sur des double
Résultat sur des int
Résultat sur des float
Résultat sur des double
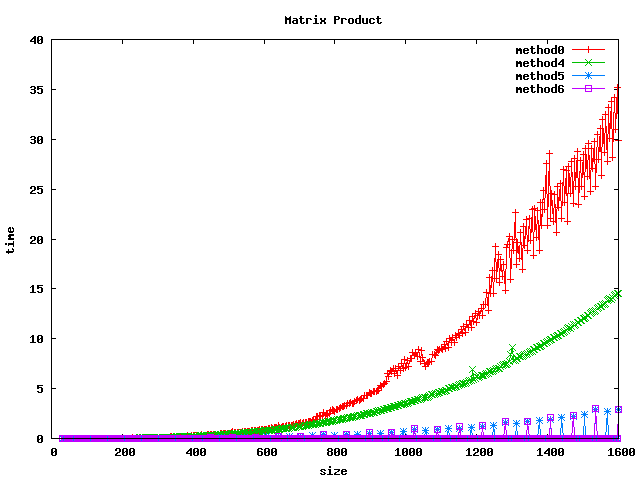
Résultat sur des int
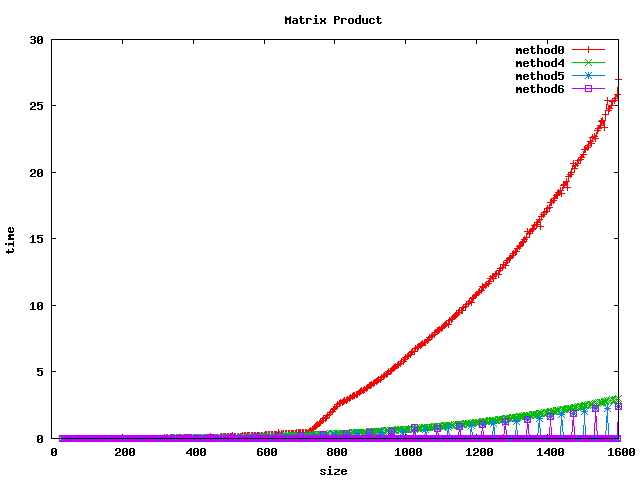
Résultat sur des float
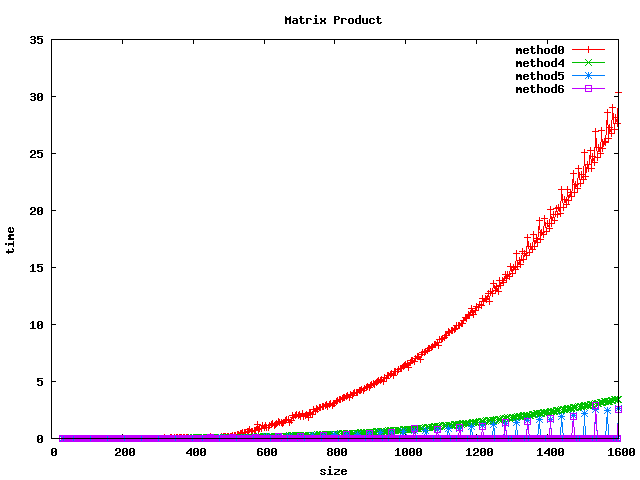
Résultat sur des double
VTune Sampling Activity reporte les valeurs suivantes :
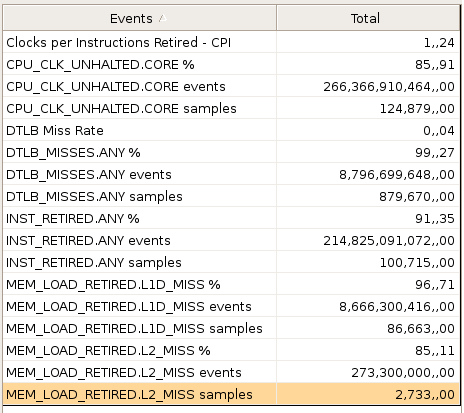
méthode "basic" - integer - 1023
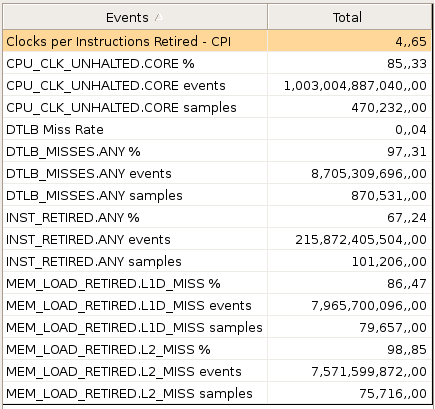
méthode "basic" - integer - 1024
| Cache / Dimension | 1023 | 1024 |
| défauts L1 | 8,6 × 109 | 7,9 × 109 |
| défauts L2 | 0,27 × 109 | 7,5 × 109 |
On voit que le problème provient du cache L2 (MEM_LOAD_RETIRED.L2_MISS events) :
- 1023 : 273 106
- 1024 : 7.571 106 (soit un facteur 27)
VTune Sampling Activity reporte les valeurs suivantes :
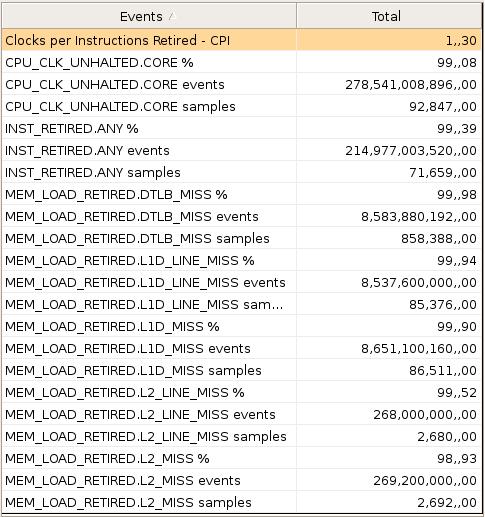
méthode "basic" - integer - 2047
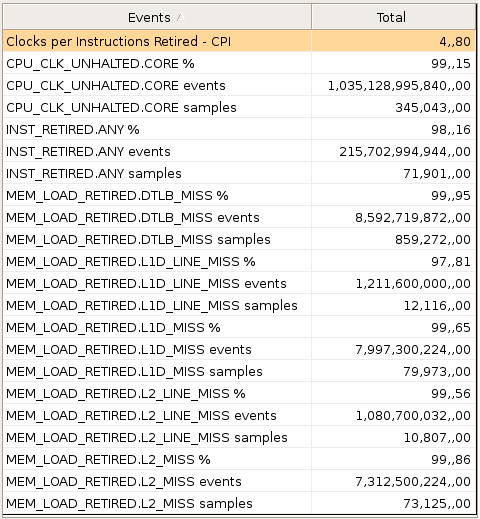
méthode "basic" - integer - 2048
| Cache / Dimension | 2047 | 2048 |
| défauts L1 | 8,6 × 109 | 7,9 × 109 |
| défauts L2 | 0,26 × 109 | 7,3 × 109 |
On voit que le problème provient du cache L2 (MEM_LOAD_RETIRED.L2_MISS events) :
- 2047 : 269 106
- 2048 : 7.312 106 (× 27)
Le manque de performance de l'algorithme basic provient d'un nombre important de défauts de cache (cache misses). L'accès à la mémoire n'est pas réalisé de manière "intelligente" et celle-ci n'est donc pas utilisée à bon escient. Il nous faut donc augmenter la réutilisabilité des données du cache.
Si l'on examine le code on s'aperçoit que A est accédée par ligne (row-major order) alors que B est accédée par colonnes (column-major order).
- l'accès par ligne est moins pénalisant car on accède à des données contigües.
- par contre l'accès par colonne est pénalisant notamment si une ligne est de grande taille
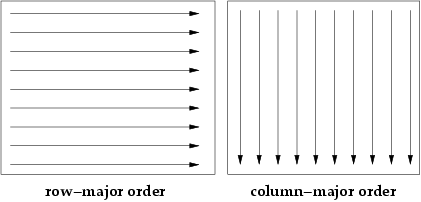
L'accès à la matrice B génère donc de nombreux défauts de cache.
Une technique simple appelée loop blocking consiste à décomposer le problème initial en sous-problèmes de plus petite taille. Dans le cas présent on peut décomposer la matrice en sous-matrices de taille 32 × 32.