Ce site est en cours de reconstruction certains liens peuvent ne pas fonctionner ou certaines images peuvent ne pas s'afficher.

stacks

counter_1 accueil counter_2 cours counter_3 travaux pratiques

4. TP - Zéro d'une fonction

4.1. Introduction

Dans ce TP on cherche une valeur pour laquelle une fonction réelle d'une variable s'annule.

Soit $f(x)$ de $ℝ$ dans $ℝ$, on cherche $x_0$ tel que $f(x_0) = 0$.

Il existe plusieurs méthodes pour résoudre ce problème, nous allons étudier les méthodes suivantes :

méthode par dichotomie
méthode de la sécante
méthode de la tangente

Pour chacune de ces méthodes on considérera que l'on est dans un intervalle $[a,b]$ sur lequel la fonction s'annule et que le produit $f(a) × f(b) < 0$.

4.2. Méthode par dichotomie

Cette méthode consiste à prendre le milieu de l'intervalle $[a,b]$ défini par :

$$m = (a + b) / 2$$

si $f(a) × f(m) < 0$ alors cela signifie que $x_0$ est dans l'intervalle $[a,m]$
si $f(m) × f(b) < 0$ alors cela signifie que $x_0$ est dans l'intervalle $[m,b]$

On remplace alors $b$ par $m$ (ou dans le second cas $a$ par $m$) et on continue jusqu'à trouver une valeur de $m$ telle que $f(m)$ soit proche de 0.

Fonction zero_dichotomie(a,b)
Entrée	a (réel) : borne inférieure b (réel) : borne supérieure
Sortie	Le zéro de la fonction $x_0$, tel que $f(x_0) = 0$
Variables locales	$m$ le milieu de l'intervalle $[a..b]$
Description	On calcule le milieu de l'intervalle $m = (a+b)/2$ et si $f(a) × f(m) < 0$ on remplace $b$ par $m$, sinon on remplace $a$ par $m$
Afficher le code ens/polytech/zero_dichotomie.algo réel x0 = (a + b) / 2 entier iterations = 0 tantque f(x0) n_est_pas_proche_de_zero faire si f(a) * f(x0) < 0 alors b = x0 sinon a = x0 fin si x0 = (a + b) / 2 iterations += 1 fin tantque retourne x0, f(x0), iterations

La seule difficulté réside dans l'expression $f(m)$ n'est pas proche de 0. Ce qui en informatique se traduit par $| f(m) | < ε$, c'est à dire que la valeur absolue est inférieure à un epsilon (petit) donné.

Exercice 4.1

Créez un fichier function.py qui contiendra :

la définition de la fonction $f(x) = x × x × sin(x)$
une constante epsilon égale à 1e-8

Exercice 4.2

Créez un fichier zero_dichotomie.py qui contiendra une fonction recherche_zero(a,b) qui implante la recherche par dichotomie du zéro de la fonction $f(x)$. Cette fonction retournera trois valeurs :

$x_0$ le zéro de la fonction
$f(x_0)$
le nombre d'itérations de calcul pour obtenir $x_0$ proche de $ε$

Exercice 4.3

Créez un fichier zero.py qui recherchera $x_0$ dans l'intervalle $[6,7]$ en utilisant la recherche par dichotomie.

On affichera le résultat obtenu sous la forme nombre d'itérations, $x_0$, $f(x_0)$ :

27   6.283 -9.596572464037597e-09

4.3. Méthode de la sécante

Cette méthode consiste à trouver le point $m$ pour lequel la droite $y = vx +w$ passant par les points $(a,f(a))$ et $(b,f(b))$ s'annule

$$m = (a + b) / 2$$

si $f(a) × f(m) < 0$ alors cela signifie que $x_0$ est dans l'intervalle $[a,m]$
si $f(m) × f(b) < 0$ alors cela signifie que $x_0$ est dans l'intervalle $[m,b]$

On remplace alors $b$ par $m$ (ou dans le second cas $a$ par $m$) et on continue jusqu'à trouver une valeur de $m$ telle que $f(m)$ soit proche de 0.

En ce qui concerne la sécante, elle vérifie : $$f(a) = a × v + w$$ et $$f(b) = b × v + w$$

On a donc :

$$v = (f(b) - f(a)) / (b-a)$$

$$w = (b × f(a) - a × f(b))/ (b-a)$$

Elle coupe donc l'axe des $x$ lorsque $y = 0 = v × x + w$, soit $x = -w / v$:

$$ x = (a × f(b) - b × f(a)) / (f(b) - f(a)) $$

Fonction zero_secante
Entrée	a (entier) : borne inférieure b (entier) : borne supérieure
Sortie	Le zéro de la fonction $x_0$, tel que $f(x_0) = 0$
Variables locales	$m$ point de croisement de l'axe des $x$ avec la droite qui passe par $(a,f(a))$ et $(b, f(b))$
Description	On calcule le nombre de diviseurs de n, s'il en existe deux alors le nombre est premier
Afficher le code ens/polytech/zero_secante.algo réel x0 = (a * f(b) - b * f(a)) / (f(b) - f(a)) entier iterations = 0 tantque f(x0) n_est_pas_proche_de_zero faire si f(a) * f(x0) < 0 alors b = x0 sinon a = x0 fin si x0 = (a * f(b) - b * f(a)) / (f(b) - f(a)) iterations += 1 fin tantque retourne x0, f(x0), iterations

Exercice 4.4

Créez un fichier zero_secante.py qui contiendra une fonction recherche_zero(a,b) qui implante la recherche du zéro de la fonction $f(x)$ par la méthode de la sécante. Cette fonction retournera trois valeurs :

$x_0$ le zéro de la fonction
$f(x_0)$
le nombre d'itérations de calcul pour obtenir $x_0$ proche de $ε$

Exercice 4.5

Modifiez le fichier zero.py qui recherchera $x_0$ dans l'intervalle $[6,7]$ en utilisant la recherche par utilisation de la méthode de la sécante.

On affichera le résultat obtenu sous la forme nombre d'itérations, $x_0$, $f(x_0)$ :

10   6.283 -1.2606612952820044e-09

4.4. Méthode de la tangente

Cette méthode consiste à trouver le point $m$ pour lequel la tangente à la courbe s'annule.

L'équation de la tangente en un point $m$ est $y = f(m) + f'(m)(x-m)$, où $f'$ est la dérivée de $f$.

La tangente en un point d'abscisse $m$ coupe donc l'axe des $x$ en un point $x_t = m - {f(m)} / {f'(m)}$.

On commencera en prenant $m = (a + b) / 2$.

Fonction zero_tangente
Entrée	a (entier) : borne inférieure b (entier) : borne supérieure
Sortie	Le zéro de la fonction $x_0$, tel que $f(x_0) = 0$
Variables locales	$m$ point qui évolue et se rapproche de $x_0$
Description	On commence avec $m = (a+b)/2$ puis on itère en utilisant $m = m - ({f(m)} / {f'(m)})$
Afficher le code ens/polytech/zero_tangente.algo réel x0 = (a + b) / 2 entier iterations = 0 tant que f(x0) n_est_pas_proche_de_zero faire x0 = x0 - (f(x0) / f_prime(x0) ) iterations += 1 fin tant que retourne x0, f(x0), iterations

Exercice 4.6

Créez un fichier zero_tangente.py qui contiendra une fonction recherche_zero(a,b) qui implante la recherche du zéro de la fonction $f(x)$ par la méthode de la tangente. Cette fonction retournera trois valeurs :

$x_0$ le zéro de la fonction
$f(x_0)$
le nombre d'itérations de calcul pour obtenir $x_0$ proche de $ε$

Pour le calcul de la dérivée on pourra utiliser l'une des méthodes suivantes :

la formule de la dérivée : $$f'(x) = {f(x + ε) - f(x)}/ ε$$
le calcul par Python en utilisant sympy (Symbolic Python) :
Afficher le code ens/polytech/calcul_derivee.py
1. import math
2. from sympy import *
4. x = symbols('x')
5. f_prime = diff(x*x*sin(x),x)
7. print("f'(x) = ", f_prime)

Exercice 4.7

Modifiez le fichier fonction.py pour y inclure la fonction f_prime(x) qui calcule la dérivée de $f(x)$ en $x$.

Exercice 4.8

Modifiez le fichier zero.py qui recherchera $x_0$ dans l'intervalle $[6,7]$ en utilisant la recherche par utilisation de la méthode de la tangente.

On affichera le résultat obtenu sous la forme nombre d'itérations, $x_0$, $f(x_0)$ :

 4   6.283 -9.669423550915769e-15

4.5. Recherche des zéros de la fonction $f(x) = x × x × sin(x)$

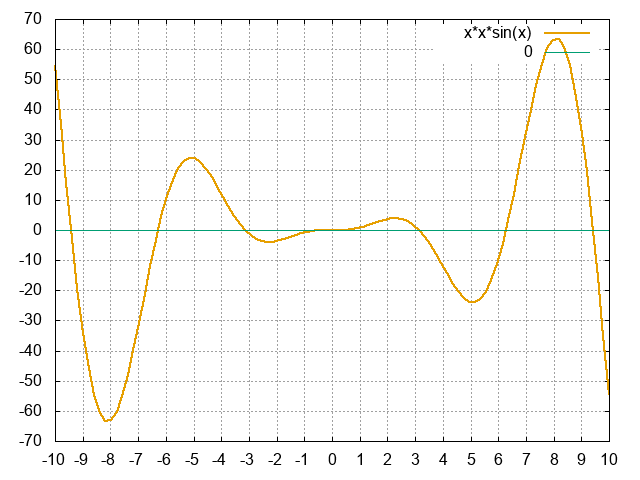
On va chercher à déterminer les zéros de la fonction $f(x) = x × x × sin(x)$.

On voit sur le graphe de la fonction qu'elle possède sur l'intervalle $[0,10]$ plusieurs valeurs qui l'annulent :

en 0
entre 3 et 4 : $x_0 = π$
entre 6 et 7 : $x_0 = 2π$
entre 9 et 10: $x_0 = 3π$
etc

x*x*sin(x)

4.5.1. Programme de recherche des zéros

Ecrire un programme qui permet de rechercher les zéros d'une fonction dans un intervalle donné, par exemple dans l'intervalle $[1,10]$ en créant un échantillon de la fonction.

Exercice 4.9

Créez le fichier recherche_zeros.py qui dans la fonction main :

créez deux listes
- x pour un ensemble de valeurs sur l'axe $x$
- et y qui correspond à l'application de $f(x)$ sur x
remplir ces listes avec 200 valeurs :
- $x_i = (b-a)/200×i$, avec $a=1$ et $b=10$ par exemple
- et $y_i = f(x_i)$
déterminer les couples $(x_i,x_{i+1})$ pour lesquels la fonction change de signe, c'est à dire que $f(x_i) × f(x_{i+1}) < 0$
rechercher les zéros de la fonction dans les intervalles $(x_i,x_{i+1})$ en utilisant les trois méthodes : dichotomie, sécante, tangente, et affichez les résultats

# couples pour lesquels on a un changement de signe
couples=
[3.1149999999999967,3.1599999999999966]
[6.264999999999992,6.309999999999992]
[9.414999999999987,9.459999999999987]
-------
21    3.141592653990 -3.947792666575956e-09
 3    3.141592653105 4.78155713480832e-09
 2    3.141592653663 -7.231299248703638e-10
-------
22    6.283185307384 8.051428253826363e-09
 3    6.283185307089 -3.5600101956497364e-09
 2    6.283185307191 4.354837022944175e-10
-------
19    9.424777960777 -7.00701446781003e-10
 3    9.424777960742 2.3924060045678592e-09
 3    9.424777960769 3.263430448434072e-14

On a trouvé trois racines dans l'intervalle $[1,10]$, soit $π$, $2π$, $3π$ :

le premier intervalle est $[3.1149999999999967,3.1599999999999966]$
le second est $[6.264999999999992,6.309999999999992]$
le triosième est $[9.414999999999987,9.459999999999987]$

4.5.2. Anomalie

Dans le cas de la méthode de la tangente, il faut être proche du zéro pour en obtenir la valeur exacte. En d'autres termes, l'intervalle de recherche initial $[a,b]$ doit se situer proche de $x_0$.

Essayez de trouver un des $x_0$ de la fonction $x × x × sin(x)$ en partant de la valeur 5. Quel résultat obtenez vous et pourquoi ?

Par exemple le programme suivant qui utilise le package scipy (pour Scientific Python et la fonctionalité fsolve qui recherche les racines d'une fonction) :

Afficher le code ens/polytech/zero_tangente_anomalie.py

import math
from scipy.optimize import fsolve
 
def f(x):
  return x*x*math.sin(x)
  
 
# provoque une erreur
x_initial = 5
print("valeur initiale pour la recherche = ", x_initial)
x_0 = fsolve(f, x_initial)
print("x_0=", x_0)
 

donne comme résultat :

..scipy/optimize/minpack.py:162: RuntimeWarning:
The number of calls to function has reached maxfev = 400.
  warnings.warn(msg, RuntimeWarning)
x_0= [-6.09065521e-50]